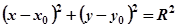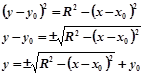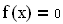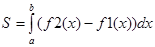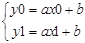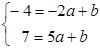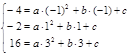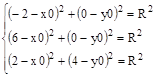ПрограммаMathcad позволяет строить графики в декартовых и полярных координатах. Можно строить двумерные и трехмерные графики.
- Построение графиков в декартовой системе координат
При построении графика сначала должна быть определена независимая переменная. Например, если график строится для всех 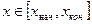
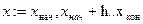
если шаг изменения переменной h. Промежуток изменения переменной можно не задавать, тогда по умолчанию будет строиться график на отрезке 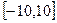
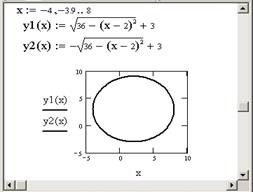
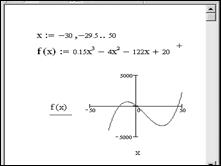
Пусть необходимо построить график функции
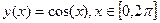
В Mathcad-документе определяются пределы изменения аргумента и сама функция
Далее определяется расположение графика в Mathcad-документе и в меню Insert активизируется в подменю Graph команда X-Y Plot . В области графика в ячейке рядом с осью абсцисс указывается имя независимой переменной, а в ячейке рядом с осью ординат — имя функции.
Если необходимо представить в одном окне два или более графика, то в ячейку рядом с осью ординат вводятся через запятую необходимых имена функций. При этом кривые графиков представляются различным цветом.
Например, необходимо построить два графика функций 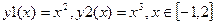
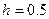
- Построение графиков в полярной системе координат
В программе Mathcad возможно строить графики функций, заданных в полярной системе координат.
В случае, когда начало декартовой системы, совмещено с полюсом, а полярная ось с 0х, то координаты точки 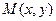
Если функция, график которой следует построить, задана полярным уравнением, т.е. 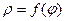
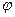
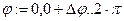
Задать функцию пользователя
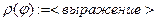
Для ввода греческих букв используется панель Greek(меню View, подменю Toolbars).
Далее в меню Insert в подменю Graph активизируется команда Polar Plot. В Mathcad-документе появляется графическая область. В нижнюю область в ячейку вводится имя полярного угла, а в левую — имя функции 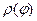
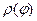
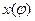
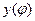
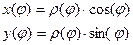
можно записать уравнение, заданное в полярных координатах, в декартовых координатах.
Пример 1.
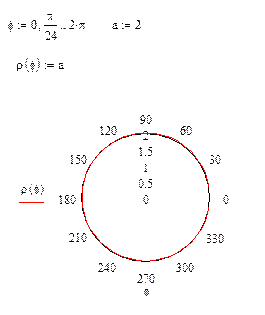
Уравнение 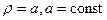
Уравнение в декартовой системе для этой окружности можно записать;
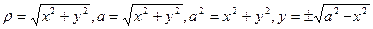
Если построить график в декартовой системе координат, то получим окружность с центром в начале координат.
Пример 2.
Задано уравнение 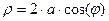
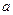
В полярных координатах график будет иметь вид
Лекция 4.
- Вычисления с векторами и матрицами
Mathcad имеются мощные возможности выполнения операций с векторами и матрицами. При этом операции можно производить как символами, так и численно.
Дата добавления: 2015-12-26 ; просмотров: 7831 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
- Построение графиков в MathCad
- Построение графика по точкам
- Построение графика функции f(x)
- Построение эпюры в mathcad
- Построение графика в полярных координатах в mathcad
- Учебное пособие: Пособие MathCAD
- 1. Рабочее окно MathCAD
- 2. Элементы языка MathCAD
- 3. Форматирование чисел
- 5. Работа с графикой
- 5.1 Построение двухмерных графиков
- 5. 2 Построение полярных графиков
- 5. 3 Построение графиков поверхностей (трехмерные или 3D-графики)
- 6. Способы решения уравнений в MathCAD
- 6.1 Решение уравнений с помощью функции root(f(x),x)
- 6.2 Решение уравнений с помощью функции Polyroots(v)
- 7. Решение систем уравнений
- 7.1 Решение систем линейных уравнений
- 7. 2 Решение систем нелинейных уравнений
- 8 . Примеры использования основных возможностей MathCAD для решения некоторых математических задач
- 8.1 Нахождение локальных экстремумов функций
- 8.3 Построение кривых по заданным точкам
Видео:Уравнение окружности (1)Скачать

Построение графиков в MathCad
В статье рассмотрены основные возможности построения графиков в программе mathcad. Для инженерных и студенческих расчетов, как правило, достаточно знать следующие методы построения графиков:
Видео:MathCAD. Given - FindСкачать

Построение графика по точкам
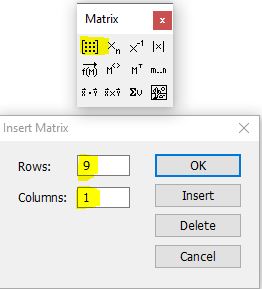
Чтобы построить график по точкам в декартовой системе координат необходимо задаться исходными данными. Создадим две матрицы-столбца, назовем их X и Y соответственно и заполним их значениями. Для создания матриц-столбцов воспользйтесь панелью Matrix. В панели matrix нажмите на кнопку под названием Matrix and vector. В появившемся окне введите количество строк и столбцов. Для матрицы-столбца количество столбцов будет очевидно ровно одному. Количество строк зависит от количества точек. В нашем случае это 9 точек. После внесения данных нажмите ОК (см. рис. 1)
Рис. 1. Создание матриц-столбцов
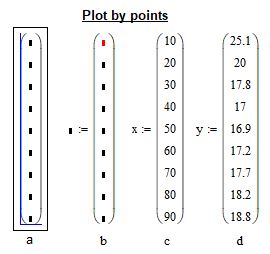
В свободном поле mathcad появится пустая матрица-столбец. Поместите курсор в матрицу и с использованием клавиш «стрелка» и «пробел» добейтесь положения курсора, как показано на рисунке 2а ниже. После чего введите с клавитуры символ двоеточия «:«. У вас должна получиться маска как на рисунке 2b. Теперь вы можете присводить содержимое матрицы какой то переменной. Например переменной X (см. рис. 2c). Заполните матрицу в соответсвии с рисунком 2 и затем повторите те же самые действия для создания матрицы-столбца Y.
Рис. 2. Заполнение матриц-столбцов для графика
На панели Graph найдите кнопку X-Y plot и щелкните по ней левой кнопкой мыши. У вас появится маска для построения графика. В черных прямоугольниках можно вводить имена осей абсцисс и ординат, а так же область отображения кривой графика (см. рис. 3)
Рис. 3. Создание заготовки для графика
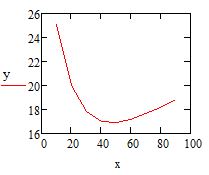
Введите под осью абсцисс имя матрицы-столбца X, а слева от оси ординат имя матрицы-столбца Y. В окне графика вы увидите ломаную линию, соединящие координаты, указанные в матрицах столбцах (см. рис. 4)
Рис. 4. График по точкам
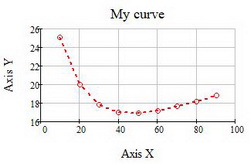
Оформление кривой графика по умолчанию, как правило, лишено наглядности и читабельности. Средства mathcad позволяют настраивать отображение графиков. Для этого щелкните 2 раза левой кнопкой мыши по изображению графика и в появившемся окне настройте внешний вид кривой, координатных осей и прочих элементов. Возможности mathcad позволяют: изменять цвет линий, их толщину и тип; нанести сетку на поле графика; подписывать оси координат; изменять формат числовых данных; вводить дополнительную (вторичную, второстепенную) ось ординат. После настройки всех элементов нажмите ОК и вы заметите, что ваш график приобрел более привлекательный вид (см. рис. 5)
Рис. 5. Настройка отображения графика
Видео:MathCAD Построение графика быстрым способомСкачать
Построение графика функции f(x)
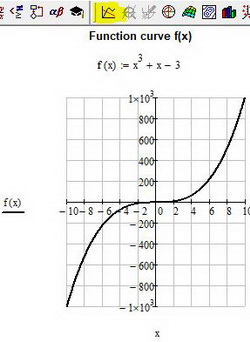
Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой
Рис. 6. Построение графика функции f(x)
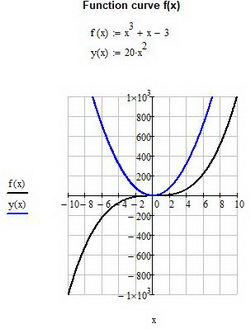
Чтобы построить два графика и более на одном поле (в тех же осях координат) сделайте следующее: введите вторую функцию, например y(x):=. , поместите курсор мыши в маркер поля графика, где уже указана первая функция f(x) и введите запятую. Таким образом mathcad зоздаст второй маркер для ввода очередной функции. Введите вашу вторую функцию и нажмите enter. Если имя аргумента обеих функций совпадает, то вторая кривая отобразится в поле графика, в противном случае, под осью абсцисс введите через запятую имя аргумента второй функции. Образец можно посмотреть ниже на рис. 7

Рис. 7. Построение двух графиков функции
Видео:Mathcad-09. Пример: уравненияСкачать

Построение эпюры в mathcad
Чтобы построить классическую эпюру в mathcad нужно выполнить следующие действия:
— ввести функцию в виде y = f(x), как это показано в примерах выше;
— ввести такназываемую ранжинрованную переменную в виде i = a, a-dt..b с определенным шагом dt;
— создать поле графика и ввести туда функции f(x) и f(i) с соответствующими аргументами
— настроить визуализацию функции f(i) в соответствии с требованиями к оформлению эпюр в вашем ВУЗе или компании
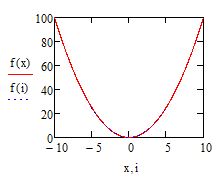
Ранжированная переменная по сути является матрицей-столбцом, разница лишь в том, что значение элементов в нее входящих представляют из себя определенную закономерность или последовательность чисел. Ранжированную переменную можно ввести воспользовавшись кнопкой Range Variable из панели Matrix. Первый маркер отвечает за начальное значение последовательности, второй — за конечное. По умолчаию шаг последовательности равен 1. Если после первого элемента ввести символ запятой и в появившемся маркере ввести следующее число вашей последовательности, то таким образом вы определите шаг, с которым будет заполняться ваша последовательность. Обратите внимание на пример ниже.
Рис. 8. Ввод ранжированной переменной
Ранжированные переменные можно использовать для построения эпюр распределения физических величин. Для этого постройте ваш исходный график одним из методов, описанных выше. Пусть это будет график f(x):=x^2. Затем создайте ранжированную переменную с шагом 0.5 как указано в примере ниже
Рис. 9. Ввод ранжированной переменной
Далее создайте поле для графика и около оси ординат введите две функции: f(x) и f(i). Под осью абсцисс также введите соответсвующие аргументы: x и i. Вы должны увидет обычную параболу как на рисунке ниже
Рис. 10. Построение эпюры. Шаг 1
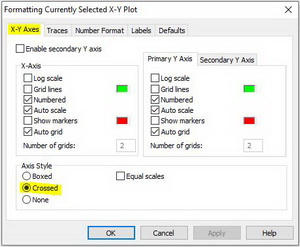
Для получения эпюры нужно настроить отображение функции f(i) в свойствах графика. Щелкните 2 раза по графику чтобы вызвать меню настройки отображения графика. Перейдите во вкладку traces. В списке Legend Label найдите имя trace 2. В столбце Type для trace 2 из выпадающего списка выберете тип графика stem. В столбце Symbol уберите отображение элементов. Во вкладке X-Y Axes выберете для Axis Style тип Crossed. Нажмите ОК и вы увидете эпюру. Вы можете настроить ее внешний вид по желанию.
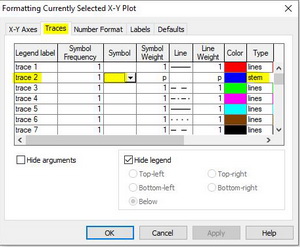
Рис. 11. Построение эпюры. Шаг 2
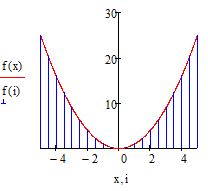
В итоге вы увидите, что на графике появились вертикальные линии, которые распределены по оси абсцисс с шагом, который вы указали в ранжированной переменной. Изменяя параметры этой переменной можно настроить отображение эпюры. Эпюра готова (см. рис. 12)
Рис. 12. Построение эпюры. Шаг 3
Видео:Уравнение окружности и ее графикСкачать

Построение графика в полярных координатах в mathcad
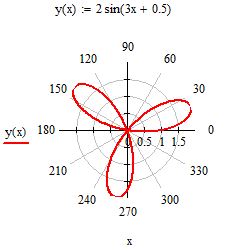
Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)
Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph
Рис. 13. Создание загатовки для графика в полярных координатах
Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.
Рис. 14. Построение графика в полярной системе координат
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Видео:Математика это не ИсламСкачать

Учебное пособие: Пособие MathCAD
| Название: Пособие MathCAD Раздел: Рефераты по информатике Тип: учебное пособие Добавлен 09:29:48 29 ноября 2010 Похожие работы Просмотров: 926 Комментариев: 21 Оценило: 4 человек Средний балл: 4.8 Оценка: неизвестно Скачать |

Рис. 2.1. Шаблон двухмерного графика
щелкнуть мышью вне шаблона графика — график функции будет построен.
Диапазон изменения аргумента состоит из 3-х значений: начальное, второе и конечное.
Пусть необходимо построить график функции на интервале [-2,2] с шагом 0.2. Значения переменной t задаются в виде диапазона следующим образом:
где: –2 — начальное значение диапазона;
–1.8 (–2 + 0.2) — второе значение диапазона (начальное значение плюс шаг);
2 — конечное значение диапазона.
Внимание. Многоточие вводится нажатием точки с запятой в английской раскладке клавиатуры.
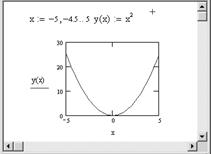
Пример. Построение графика функции y = x 2 на интервале [–5,5] с шагом 0.5 (рис. 2.2).
Рис. 2.2. Построение графика функции y = x 2
При построении графиков необходимо учитывать следующее:
° Если диапазон значений аргумента не задан, то по умолчанию график строится в диапазоне [–10,10].
° Если в одном шаблоне необходимо разместить несколько графиков, то имена функций указываются через запятую.
° Если две функции имеют различные аргументы, например f1(x) и f2(y), то на оси ординат (Y) через запятую указываются имена функций, а по оси абсцисс (X) — имена обеих переменных тоже через запятую.
° Крайние метки данных на шаблоне графика служат для указания предельных значений абсцисс и ординат, т.е. они задают масштаб графика. Если оставить эти метки незаполненными, то масштаб будет установлен автоматически. Автоматический масштаб не всегда отражает график в нужном виде, поэтому предельные значения абсцисс и ординат приходится редактировать, изменяя вручную.
Примечание. Если после построения график не принимает нужный вид, можно:
· изменить интервал построения графика.
· уменьшить на графике предельные значения абсцисс и ординат.
Пример. Построение окружности с центром в точке (2,3) и радиусом R = 6.
Уравнение окружности с центром в точке с координатами (x 0 ,y 0 ) и радиусом R записывается в виде:
Выразим из этого уравнения y :
Таким образом, для построения окружности необходимо задать две функции: верхнюю и нижнюю полуокружности. Диапазон значений аргумента вычисляется следующим образом:
— начальное значение диапазона = x 0 – R ;
— конечное значение диапазона = x 0 + R ;
— шаг лучше взять равным 0.1 (рис. 2.3.).
Рис. 2.3. Построение окружности
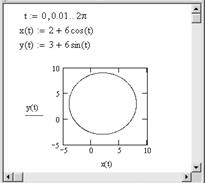
Параметрический график функции
Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты x и y , рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат x и y в виде функций от некоторой переменной величины t (параметра): x (t ) и y (t ). При построении параметрического графика на осях ординат и абсцисс указываются имена функций одного аргумента.
Пример. Построение окружности с центром в точке с координатами (2,3) и радиусом R = 6. Для построения используется параметрическое уравнение окружности
Рис.2.4. Построение окружности
Чтобы отформатировать график, необходимо дважды щелкнуть по области графика. Откроется диалоговое окно форматирования графика. Ниже перечислены вкладки окна форматирования графика:
— X — Y Axes — форматирование осей координат. Установив нужные флажки можно:
· Log Scale — представить численные значения на осях в логарифмическом масштабе (по умолчанию численные значения наносятся в линейном масштабе)
· Grid Lines — нанести сетку линий;
· Numbered — расставить числа по координатным осям;
· Auto Scale — автоматический выбор предельных численных значений на осях (если этот флажок снят, предельными будут максимальные вычисленные значения);
· Show Marker — нанесение меток на график в виде горизонтальных или вертикальных пунктирных линий, соответствующих указанному значению на оси, причем сами значения выводятся в конце линий (на каждой оси появляются 2 места ввода, в которые можно ввести численные значения, не вводить ничего, ввести одно число или буквенные обозначения констант);
· Auto Grid — автоматический выбор числа линий сетки (если этот флажок снят, надо задать число линий в поле Number of Grids);
· Crossed — ось абсцисс проходит через нуль ординаты;
· Boxed — ось абсцисс проходит по нижнему краю графика.
— Trace — форматирование линии графиков функций. Для каждого графика в отдельности можно изменить:
· символ (Symbol) на графике для узловых точек (кружок, крестик, прямоугольник, ромб);
· вид линии (Solid — сплошная, Dot — пунктир, Dash — штрихи, Dadot — штрих-пунктир);
· цвет линии (Color);
· тип (Туре) графика (Lines — линия, Points — точки, Ваr или Solidbar — столбики, Step — ступенчатый график и т.д.);
· толщину линии (Weight).
— Label — заголовок в области графика. В поле Title (Заголовок) можно записать текст заголовка, выбрать его положение — вверху или внизу графика (Above — вверху, Below — внизу). Можно вписать, если надо, названия аргумента и функции (Axis Labels ).
— Defaults — с помощью этой вкладки можно вернуться к виду графика, принятому по умолчанию (Change to default), либо сделанные вами изменения на графике использовать по умолчанию для всех графиков данного документа (Use for Defaults).
Видео:Mathcad. Как задать функциюСкачать
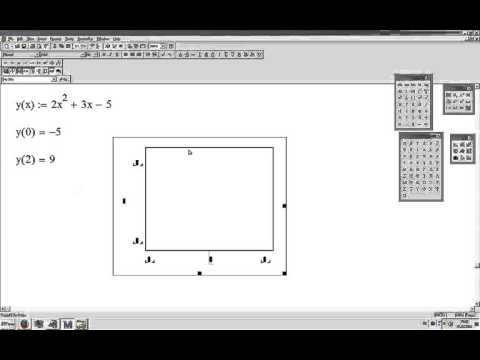
5. 2 Построение полярных графиков
Для построения полярного графика функции необходимо:
· задать диапазон значений аргумента;
· установить курсор в то место, где должен быть построен график, на математической панели выбрать кнопку Graph (график) и в открывшейся панели кнопку Polar Plot (полярный график);
· в местах ввода появившегося шаблона необходимо ввести угловой аргумент функции (внизу) и имя функции (слева).
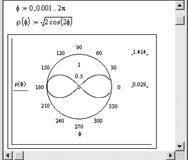
Пример . Построение лемнискаты Бернулли: 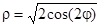

Рис.2.6. Пример построения полярного графика
Видео:Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

5. 3 Построение графиков поверхностей (трехмерные или 3D-графики)
При построении трехмерных графиков используется панель Graph (График) математической панели. Можно построить трехмерный график с помощью мастера, вызываемого из главного меню; можно построить график, создав матрицу значений функции двух переменных; можно задействовать ускоренный метод построения; можно вызвать специальные функции CreateMech и CreateSpase, предназначенные для создания массива значений функции и построения графика. Мы рассмотрим ускоренный метод построения трехмерного графика.
Быстрое построение графика
Для быстрого построения трехмерного графика функции необходимо:
· установить курсор в то место, где должен быть построен график, на математической панели выбрать кнопку Graph (График) и в открывшейся панели кнопку 
· в единственное место шаблона введите имя функции (не указывая переменные);
· щелкнуть мышью вне шаблона графика — график функции будет построен.
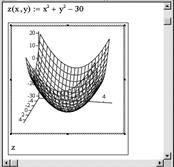
Пример. Построение графика функции z (x ,y ) = x 2 + y 2 – 30 (рис. 2.7).
Рис. 2.7. Пример быстрого построения поверхностного графика
Построенным графиком можно управлять:
° вращение графика выполняется после наведения на него указателя мыши при нажатой левой кнопке мыши;
° масштабирование графика выполняется после наведения на него указателя мыши при одновременном нажатии левой кнопки мыши и клавиши Ctrl (если двигать мышь, график приближается или удаляется);
° анимация графика выполняется аналогично, но при нажатой дополнительно клавише Shift. Необходимо только начать вращение графика мышью, дальше анимация будет выполняться автоматически. Для остановки вращения следует щелкнуть левой кнопкой мыши внутри области графика.
Существует возможность построения сразу нескольких поверхностей на одном рисунке. Для этого необходимо задать обе функции и через запятую указать имена функций на шаблоне графика.
При быстром построении графика по умолчанию выбираются значения обоих аргументов в пределах от –5 до +5 и число контурных линий, равное 20. Для изменения этих значений необходимо:
· дважды щелкнуть по графику;
· в открывшемся окне выбрать вкладку Quick Plot Data;
· ввести новые значения в области окна Range1 — для первого аргумента и Range2 — для второго аргумента (start — начальное значение, end — конечное значение);
· в поле # of Grids изменить число линий сетки, покрывающих поверхность;
· щелкнуть на кнопке Ок.
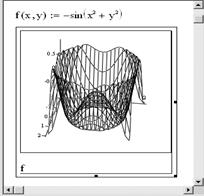
Пример . Построение графика функции z (x ,y ) = –sin(x 2 + y 2 ) (рис. 2.9).
При построении этого графика пределы изменения значений обоих аргументов лучше выбрать от –2 до +2.
Рис. 2.9. Пример построения графика функции z (x ,y ) = –sin(x 2 + y 2 )
Форматирование трехмерных графиков
Для форматирования графика необходимо дважды щелкнуть по области построения — появится окно форматирования с несколькими вкладками: Appearance , General , Axes , Lighting , Title , Backplanes , Special , Advanced , Quick Plot Data .
Назначение вкладки Quick Plot Data было рассмотрено выше.
Вкладка Appearance позволяет менять внешний вид графика. Поле Fill Options позволяет изменить параметры заливки, поле Line Option — параметры линий, Point Options — параметры точек.
Во вкладке General ( общие) в группе View можно выбрать углы поворота изображенной поверхности вокруг всех трех осей; в группе Display as можно поменять тип графика.
Во вкладке Lighting (освещение) можно управлять освещением, установив флажок Enable Lighting (включить освещение) и переключатель On (включить). Одна из 6-ти возможных схем освещения выбирается в списке Lighting scheme (схема освещения).
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

6. Способы решения уравнений в MathCAD
В данном разделе мы узнаем, каким образом в системе MathCAD решаются простейшие уравнения вида F(x ) = 0. Решить уравнение аналитически — значит найти все его корни, т.е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Решить уравнение графически — значит найти точки пересечения графика функции с осью ОХ.
Видео:Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

6.1 Решение уравнений с помощью функции root(f(x),x)
Для решений уравнения с одним неизвестным вида F(x ) = 0 существует специальная функция
где f (x ) — выражение, равное нулю;
Эта функция возвращает с заданной точностью значение переменной, при котором выражение f (x ) равно 0.
Внимание. Если правая часть уравнения ¹0, то необходимо привести его к нормальному виду (перенести все в левую часть).
Перед использованием функции root необходимо задать аргументу х начальное приближение. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.
Внимание. Перед решением желательно построить график функции, чтобы проверить, есть ли корни (пересекает ли график ось Ох), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.
Пример. Решение уравнения 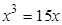
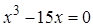
Рис. 3.1. Решение уравнения при помощи функции root
Видео:УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать

6.2 Решение уравнений с помощью функции Polyroots(v)
Для одновременного нахождения всех корней полинома используют функцию Polyroots ( v ), где v — вектор коэффициентов полинома, начиная со свободного члена. Нулевые коэффициенты опускать нельзя. В отличие от функции root функция Polyroots не требует начального приближения.
Пример . Решение уравнения 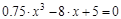
Рис. 3.2. Решение уравнения с помощью функции polyroots
6. 3 Решение уравнений с помощью функции Find ( x )
Функция Find (Найти) работает в ключевой связке с ключевым словом Given (Дано). Конструкция Given – Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Если задано уравнение f (x ) = 0, то его можно решить следующим образом с помощью блока Given – Find :
– задать начальное приближение
– ввести служебное слово
– записать уравнение, используя знак жирное равно
– написать функцию find с неизвестной переменной в качестве параметра
В результате после знака равно выведется найденный корень.
Если существует несколько корней, то их можно найти, меняя начальное приближение х0 на близкое к искомому корню.
Пример. Решение уравнения 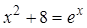
Рис. 3.3. Решение уравнения с помощью функции find
Иногда возникает необходимость отметить на графике какие-либо точки (например, точки пересечения функции с осью Ox). Для этого необходимо:
· указать значение x данной точки (по оси Ох) и значение функции в этой точке (по оси Оy);
· дважды щелкнуть по графику и в окне форматирования во вкладке Traces для соответствующей линии выбрать тип графика — points, толщину линии — 2 или 3.
Пример. На графике отмечена точка пересечения функции 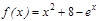
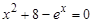
Рис. 3.4. График функции 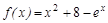
В окне форматирования графика во вкладке Traces для trace 2 изменены: тип графика — points, толщина линии — 3, цвет — черный.
Видео:Составляем уравнение окружностиСкачать

7. Решение систем уравнений
7.1 Решение систем линейных уравнений
Систему линейных уравнений можно решить матричным методом (или через обратную матрицу или используя функцию lsolve (A,B)) и с использованием двух функций Find и функции Minerr .
Пример. Дана система уравнений:
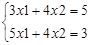
Решение данной системы уравнений матричным методом представлено на рисунке 4.1.
Рис. 4.1. Решение системы линейных уравнений матричным методом
Lsolve (A,B) — это встроенная функция, которая возвращает вектор Х для системы линейных уравнений 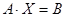
Пример . Дана система уравнений:
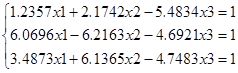
Способ решения данной системы с использованием функции lsolve(A,B) приведен на рисунке 4.2.
Рис. 4.2. Решение системы линейных уравнений с использованием функции lsolve
Решение системы линейных уравнений с помощью функции Find
При данном методе уравнения вводятся без использования матриц, т.е. в «натуральном виде». Предварительно необходимо указать начальные приближения неизвестных переменных. Это могут быть любые числа, входящие в область определения. Часто за них принимают столбец свободных членов.
Для того чтобы решить систему линейных уравнений с помощью вычислительного блока Given – Find , необходимо:
1) задать начальные приближения для всех переменных;
2) ввести служебное слово Given ;
3) записать систему уравнений, используя знак жирное равно (= );
4) написать функцию Find , перечислив неизвестные переменные в качестве параметров функции.
В результате расчетов выведется вектор решения системы.
Пример. Дана система уравнений:
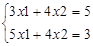
Решение данной системы с помощью вычислительного блока Given – Find приведено на рисунке 4.3.
Рис. 4.3. Решение системы линейных уравнений с помощью функции Find
Приближенное решение системы линейных уравнений
Решение системы линейных уравнений с помощью функцию Minerr аналогично решению с помощью функции Find (используется тот же алгоритм), только функция Find дает точное решение, а Minerr — приближенное. Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Miner r возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке.
Общие рекомендации по решению уравнений и систем уравнений
Ниже перечислены некоторые рекомендации, которые следует выполнять, если MathCAD не может самостоятельно найти решение.
· Можно подобрать другое начальное приближение.
· Можно увеличить или уменьшить точность расчетов. Для этого в меню выбрать Math ► Options (Математика – Опции), вкладка Built — In Variables (Встроенные переменные). В открывшейся вкладке необходимо уменьшить допустимую погрешность вычислений (Convergence Tolerance (TOL)). По умолчанию TOL = 0.001.
Внимание. При матричном методе решения необходимо переставить коэффициенты согласно возрастанию неизвестных х 1, х 2, х 3, х 4.
7. 2 Решение систем нелинейных уравнений
Системы нелинейных уравнений в MathCAD решаются с помощью вычислительного блока Given – Find .
Конструкция Given – Find использует расчетную методику, основанную на поиске корня вблизи точки начального приближения, заданной пользователем.
Для решения системы уравнений с помощью блока Given – Find необходимо:
1) задать начальные приближения для всех переменных;
2) ввести служебное слово Given ;
3) записать систему уравнений, используя знак жирное равно (= );
4) написать функцию Find , перечислив неизвестные переменные в качестве параметров функции.
В результате расчетов выведется вектор решения системы.
Если система имеет несколько решений, алгоритм следует повторить с другими начальными приближениями.
Примечание. Если решается система из двух уравнений с двумя неизвестными, перед решением желательно построить графики функций, чтобы проверить, есть ли корни у системы (пересекаются ли графики заданных функций), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.
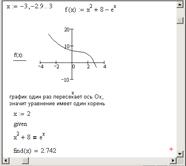
Пример . Дана система уравнений
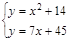
Перед решением системы построим графики функций: параболы (первое уравнение) и прямой (второе уравнение). Построение графика прямой и параболы в одной системе координат приведено на рисунке 4.5:
Рис. 4.5. Построение графика двух функций в одной системе координат
Прямая и парабола пересекаются в двух точках, значит, система имеет два решения. По графику выбираем начальные приближения неизвестных x и y для каждого решения. Нахождение корней системы уравнений представлено на рисунке 4.6.
Рис. 4.6. Нахождение корней системы нелинейных уравнений
Для того чтобы отметить на графике точки пересечения параболы и прямой, координаты точек, найденные при решении системы, введем по оси Ох (значения х ) и по оси Оу (значения у ) через запятую. В окне форматирования графика во вкладке Traces для trace 3 и trace 4 изменим: тип графика — points, толщина линии — 3, цвет — черный (рис. 4.7).
Рис. 4.7. Графики функций с отмеченными точками пересечения
8 . Примеры использования основных возможностей MathCAD для решения некоторых математических задач
В данном разделе приведены примеры решения задач, для решения которых необходимо решить уравнение или систему уравнений.
8.1 Нахождение локальных экстремумов функций
Необходимое условие экстремума (максимума и/или минимума) непрерывной функции формулируется так: экстремумы могут иметь место только в тех точках, где производная или равна нулю, или не существует (в частности, обращается в бесконечность). Для нахождения экстремумов непрерывной функции сначала находят точки, удовлетворяющие необходимому условию, то есть находят все действительные корни уравнения 
Если построен график функции, то можно сразу увидеть — максимум или минимум достигается в данной точке х . Если графика нет, то каждый из найденных корней исследуют одним из способов.
1-й способ. Сравнение знаков производной . Определяют знак производной 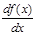
2-й способ. Вычисление второй производной . В этом случае вычисляется вторая производная 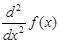
Пример. Нахождение экстремумов (минимумов/максимумов) функции 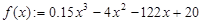
Сначала построим график функции (рис. 6.1).
Рис. 6.1. Построение графика функции
Определим по графику начальные приближения значений х , соответствующих локальным экстремумам функции f (x ). Найдем эти экстремумы, решив уравнение 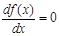
Рис. 6.2. Нахождение локальных экстремумов
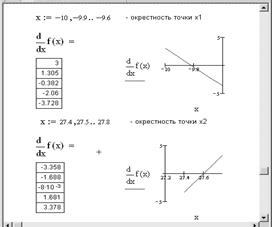
Определим вид экстремумов первым способом , исследуя изменение знака производной в окрестности найденных значений (рис. 6.3).
Рис. 6.3. Определение вида экстремума
Из таблицы значений производной и из графика видно, что знак производной в окрестности точки x 1 меняется с плюса на минус, поэтому в этой точке функция достигает максимума. А в окрестности точки x 2 знак производной поменялся с минуса на плюс, поэтому в этой точке функция достигает минимума.
Определим вид экстремумов вторым способом , вычисляя знак второй производной (рис. 6.4).
Рис. 6.4. Определение вида экстремума с помощью второй производной
Видно, что в точке x 1 вторая производная меньше нуля, значит, точка х 1 соответствует максимуму функции. А в точке x 2 вторая производная больше нуля, значит, точка х 2 соответствует минимуму функции.
Площадь криволинейной трапеции, ограниченной графиком функции f ( x ) , отрезком [a,b] на оси Ox и двумя вертикалями х = а и х = b , a 2 и y = 0.
Рис. 6.5. Нахождение площади фигуры, ограниченной линиями f (x ) = 1 – x 2 и y = 0
Площадь фигуры, заключенной между графиками функций f 1( x ) и f 2( x ) и прямыми х = а и х = b , вычисляется по формуле:
Внимание. Чтобы избежать ошибок при вычислении площади, разность функций надо брать по модулю. Таким образом, площадь будет всегда положительной величиной.
Пример . Нахождение площади фигуры, ограниченной линиями 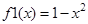
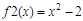
1. Строим график функций.
2. Находим точки пересечения функций с помощью функции root. Начальные приближения определим по графику.
3. Найденные значения x подставляем в формулу 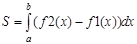
8.3 Построение кривых по заданным точкам
Построение прямой, проходящей через две заданные точки
Для составления уравнения прямой, проходящей через две точки А(x 0,y 0) и B(x 1,y 1), предлагается следующий алгоритм:
1. Прямая задается уравнением y = ax + b ,
где a и b — коэффициенты прямой, которые нам требуется найти.
Подставляем в это уравнение заданные координаты точек и получаем систему:
2. Данная система является линейной. В ней две неизвестные переменные: a и b . Систему можно решить матричным способом.
Пример. Построение прямой, проходящей через точки А(–2,–4) и В(5,7).
Подставим в уравнение прямой координаты данных точек и получим систему:
Решение этой системы в MathCAD представлено на рисунке 6.7.
Рис. 6.7.Решение системы
В результате решения системы получаем: а = 1.57, b = –0.857. Значит, уравнение прямой будет иметь вид: y = 1.57x – 0.857. Построим эту прямую (рис. 6.8).
Рис. 6.8. Построение прямой
Построение параболы, проходящей через три заданные точки
Для построения параболы, проходящей через три точки А(x 0,y 0), B(x 1,y 1) и C(x 2,y 2), алгоритм следующий:
1. Парабола задается уравнением
а , b и с — коэффициенты параболы, которые нам требуется найти.
Подставляем в это уравнение заданные координаты точек и получаем систему:
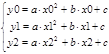
2. Данная система является линейной. В ней три неизвестные переменные: a , b и с . Систему можно решить матричным способом.
3. Полученные коэффициенты подставляем в уравнение и строим параболу.
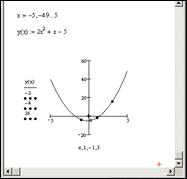
Пример. Построение параболы, проходящей через точки А(–1,–4), B(1,–2) и C(3,16).
Подставляем в уравнение параболы заданные координаты точек и получаем систему:
Решение этой системы уравнений в MathCAD представлено на рисунке 6.9.
Рис. 6.9. Решение системы уравнений
В результате получены коэффициенты: a = 2, b = 1, c = –5. Получаем уравнение параболы: 2x 2 +x –5 = y . Построим эту параболу (рис. 6.10).
Рис. 6.10. Построение параболы
Построение окружности, проходящей через три заданные точки
Для построения окружности, проходящей через три точки А(x 1,y 1), B(x 2,y 2) и C(x 3,y 3), можно воспользоваться следующим алгоритмом:
1. Окружность задается уравнением
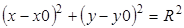
где x0,y0 — координаты центра окружности;
R — радиус окружности.
2. Подставим в уравнение окружности заданные координаты точек и получим систему:
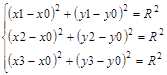
Данная система является нелинейной. В ней три неизвестные переменные: x 0, y 0 и R. Система решается с применением вычислительного блока Given – Find .
Пример . Построение окружности, проходящей через три точки А(–2,0), B(6,0) и C(2,4).
Подставим в уравнение окружности заданные координаты точек и получим систему:
Решение системы в MathCAD представлено на рисунке 6.11.
Рис. 6.11. Решение системы
В результате решения системы получено: x 0 = 2, y 0 = 0, R = 4. Подставим полученные координаты центра окружности и радиус в уравнение окружности. Получим: 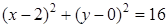
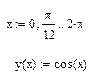
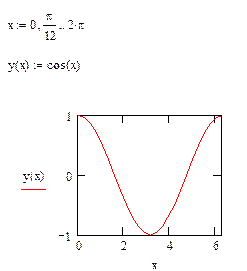
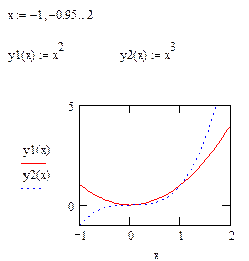
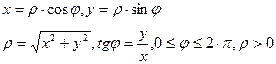
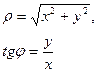
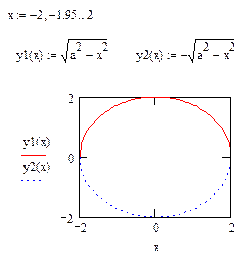
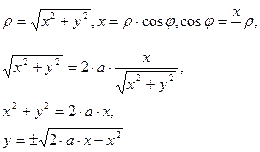
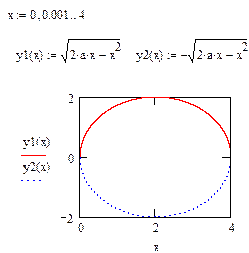


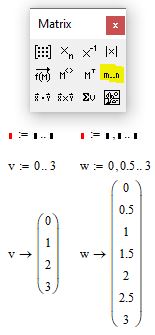




 Панель калькулятора
Панель калькулятора Панель исчислений
Панель исчислений Панель графики
Панель графики Булевая панель
Булевая панель Панель векторов и матриц
Панель векторов и матриц Панель греческих символов
Панель греческих символов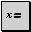 Панель оценки
Панель оценки Панель программирования
Панель программирования
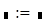 — знак присвоения (вводится нажатием клавиши : на клавиатуре (двоеточие в английской раскладке клавиатуры) или нажатием соответствующей кнопки на панели Калькулятор );
— знак присвоения (вводится нажатием клавиши : на клавиатуре (двоеточие в английской раскладке клавиатуры) или нажатием соответствующей кнопки на панели Калькулятор );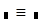 — глобальный оператор присвоения. Это присвоение может производиться в любом месте документа. К примеру, если переменной присвоено таким образом значение в самом конце документа, то она будет иметь это же значение и в начале документа.
— глобальный оператор присвоения. Это присвоение может производиться в любом месте документа. К примеру, если переменной присвоено таким образом значение в самом конце документа, то она будет иметь это же значение и в начале документа. — оператор приближенного равенства (x1). Используется при решении систем уравнений. Вводится нажатием клавиши; на клавиатуре (точка с запятой в английской раскладке клавиатуры) или нажатием соответствующей кнопки на Булевой панели.
— оператор приближенного равенства (x1). Используется при решении систем уравнений. Вводится нажатием клавиши; на клавиатуре (точка с запятой в английской раскладке клавиатуры) или нажатием соответствующей кнопки на Булевой панели.  Панели Калькулятора,
Панели Калькулятора,  Панели Исчислений и
Панели Исчислений и 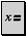 Панели Оценки.
Панели Оценки.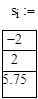 — ввод числовых значений в таблицу производится через запятую;
— ввод числовых значений в таблицу производится через запятую;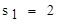 — вывод значения первого элемента вектора S;
— вывод значения первого элемента вектора S;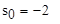 — вывод значения нулевого элемента вектора S.
— вывод значения нулевого элемента вектора S. на Панели векторов и матриц.
на Панели векторов и матриц. 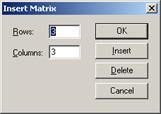

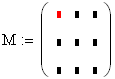

 Например :
Например :

 Щелкнуть по кнопке на панели инструментов.
Щелкнуть по кнопке на панели инструментов.