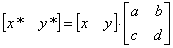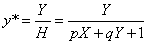ТЕМА 2. ДВУМЕРНЫЕ ПРЕОБРАЗОВАНИЯ

2.1. Общие замечания

В компьютерной графике, наряду с соответствующими алгоритмами рисования, важно иметь математический аппарат, позволяющий редактировать изображение, т. е. осуществлять его преобразование (модификацию) в соответствии с требованиями решаемой задачи. Необходимо уметь производить с графическими объектами (точками, отрезками прямых, плоскими и объемными фигурами) такие операции, как масштабирование (в том числе пропорциональное), сдвиги, симметричные отражения (относительно точки, линии, плоскости), повороты (например, относительно какой-либо точки или линии), перемещения и т. п. Подобные действия и их комбинации обычно реализуются с помощью матричных операций с данными. Краткие сведения об основах матричных преобразований, используемых при формировании двумерных сцен, приведены ниже (в рамках данной темы). Аналогичные преобразования при формировании объемных сцен кратко рассмотрены в следующей теме.

2.2. Простые преобразования точек

Точка P на плоскости однозначно определяется двумя своими координатами (x, y). В соответствие ей можно поставить матрицу-строку размером 1´2 вида (сначала будем использовать именно такое отображение точки). Следует заметить также, что точка может задаваться и соответствующей матрицей-столбцом размером 2´1. В любом случае матрицу, определяющую положение точки, часто называют координатным вектором или вектором положения.

Большинство из перечисленных выше элементарных преобразований по отношению к точке можно реализовать путем умножения матрицы на матрицу общего преобразования размером 2´2 вида :

,

где , – координаты точки P*, являющейся результатом преобразования точки P, причем .

Рассмотрим некоторые специальные случаи.

Умножение исходной матрицы на единичную 2´2 матрицу (a = d = 1, b = c = 0)

не приводит к каким-либо изменениям; поэтому подобную единичную матрицу часто называют матрицей тождественного преобразования.

– происходит так называемое локальное масштабирование (растяжение при |a| > 1 или сжатие при 0 1 или сжатие при 0 0 происходит отражение относительно оси y, при a > 0, d 1, происходит равномерное расширение, т. е. увеличение исходной фигуры, если же 0 0 осуществляет непропорциональное локальное масштабирование; неравномерное расширение и сжатие возникают в зависимости от значений (в рассматриваемом случае – положительных) a и d, которые могут быть больше или меньше, чем 1, независимо друг от друга.

2.7. Комбинированные преобразования

При модификации графического объекта часто требуется не одно простое его преобразование, а несколько последовательно проведенных преобразований. В этом случае исходную матрицу (составленную из координат точки, концов отрезка или вершин многоугольника) можно умножить на матрицу первого преобразования, полученный результат – на матрицу второго преобразования и т. д. Конечный результат будет определяться выражением

,

где – матрица n-го преобразования, n = 1, 2, …, N.

При подобных действиях следует учитывать то обстоятельство, что операция умножения матриц не является коммутативной (т. е. в общем случае ), и следует строго соблюдать порядок (последовательность) выполнения преобразований (операций умножения).

Вместе с тем, для матриц справедлив ассоциативный закон: . Поэтому для достижения того же результата можно поступить иначе: отдельные преобразования предварительно комбинировать, т. е. рассчитать матрицу полного преобразования (такую матрицу называют также композицией преобразований), и затем применить ее для преобразования исходной матрицы –

.

Продемонстрируем оба возможных подхода к комбинированному преобразованию на простом примере. Пусть требуется исходную фигуру – например, треугольник F (рис.2.8), координаты вершин которого сведены в 3´2 матрицу – повернуть на 90° вокруг точки начала координат и затем полученную промежуточную фигуру симметрично отразить относительно прямой у = – x. Первому преобразованию соответствует матрица , а второму – матрица . Осуществим последовательно соответствующие умножения:

;

очевидно, что первое умножение приводит к промежуточному результату – треугольнику F¢ (рис.2.8), второе – к конечному результату – треугольнику F* (рис.2.8).

Используем другой возможный путь комбинированного преобразования: рассчитаем матрицу полного преобразования

и умножим на нее исходную матрицу

;

результат – треугольник F* (рис.2.8) – в точности совпадает с предыдущим.

Отметим здесь, что приведенный пример очень прост: выполняются два тривиальных преобразования, результат которых можно было бы получить с помощью единственного отражения (относительно оси y). Однако он иллюстрирует изложенные выше общие положения, связанные с комбинированными преобразованиями. Далее мы будем иметь возможность познакомиться с более сложными вариантами таких преобразований.

2.8. Однородные координаты

Ранее было замечено, что использование двумерных координатных векторов, отображающих точки на плоскости, в совокупности с матрицей общего преобразования размером 2´2 накладывает ряд ограничений на модификацию объектов. В первую очередь, эти ограничения обусловлены невозможностью применения преобразования координат. Существенно расширить возможности модификации позволяет использование однородных координат для отображения точек и, соответственно, матрицы общего преобразования размером 3´3.

Однородные координаты точки P (x, y) на физической плоскости xy представляют собой тройку чисел x¢, y¢, h; первые два из них связаны с реальными координатами точки соотношениями x¢ = hx и y¢ = hy, а h – это некоторое вещественное число (отметим, что случай h = 0 является особым и будет рассмотрен ниже). Однородным координатам точки можно поставить в соответствие трехмерный координатный вектор (вектор положения) – матрицу размером 1´3 вида . Очевидно, что при таком подходе каждую точку можно связать с бесконечным множеством наборов однородных координат и, соответственно, координатных векторов вида . Вместе с тем, для точки имеется лишь один набор однородных координат со значением h = 1; ему соответствует вектор положения вида . В компьютерной графике для отображения точек (за исключением точек бесконечности, см. далее) используются координатные векторы именно такого вида.

Применяя к вектору положения исходной точки матрицу общего преобразования размером 3´3 вида , получаем:

.

Данный результат практически идентичен тому, который был получен при умножении координатного вектора на матрицу общего преобразования размером 2´2 (см. выше). Выражения для координат и преобразованной точки в обоих случаях полностью совпадают. Следовательно, использование однородных координат совместно с матрицей общего преобразования вида позволяет осуществить все те преобразования точек, отрезков и многоугольников, о которых шла речь выше (это и происходит при реальной обработке графических объектов). Задавая соответствующие значения a, b, c и d, можно реализовать тождественное преобразование, операции локального масштабирования, отражения, сдвига и поворота, аналогичные уже рассмотренным. Однако, все они, по-прежнему, будут осуществляться относительно точки начала координат.

2.9. Перемещение

Исследуем теперь дополнительные возможности, открывающиеся при новом подходе к преобразованиям. Проведем следующую матричную операцию:

;

полученный результат можно трактовать двояко: с одной стороны, можно считать, что операция привела к перемещению исходной точки вдоль осей x и y соответственно на m и n в исходной системе координат x0y (рис.2.9а); с другой стороны, можно полагать, что точка осталась на месте, а произошло преобразование координат – новая система координат x*0*y* сдвинута относительно исходной на – m вдоль оси x и на – n вдоль оси y (рис.2.9б).

В любом случае, выяснилось, что элементы m и n матрицы преобразования размером 3´3 являются коэффициентами перемещения в направлениях x и y соответственно. И не менее важный вывод из приведенного примера – теперь каждая точка плоскости, в том числе начало координат, может быть преобразована.

2.10. Поворот вокруг произвольной точки

Имея более мощный, чем ранее, математический аппарат можно реализовать и такое преобразование. Последовательность действий при этом может быть следующей:

§ объект преобразования перемещается таким образом, чтобы точка, относительно которой совершается поворот, попала в начало координат;

§ выполняется поворот объекта на требуемый угол вокруг точки начала координат;

§ осуществляется обратное перемещение объекта так, чтобы точка центра вращения возвратилась на исходное место.

Применительно координатному вектору точки подобная операция поворота вокруг точки с координатами (m, n) на произвольный угол q реализуется следующими матричными преобразованиями:

;

комбинируя три матрицы преобразования, получаем

.

Приведем простой пример рассмотренной операции: поворот отрезка L (рис.2.10), заданного однородными координатами его концов и , на 90° в положительном направлении (против часовой стрелки) вокруг точки с координатами (4, 5 ). Обобщая предыдущее выражение на случай преобразования отрезка, запишем (после подстановок в матрицу преобразования конкретных значений и расчета входящих в нее коэффициентов)

;

результат преобразования – отрезок L* (рис.2.10).

2.11. Отражение относительно произвольной прямой

В разделе 2.5 обсуждались случаи отражения относительно ряда характерных прямых, проходящих через точку начала координат. Рассмотрим теперь более сложное преобразование – симметричное отражение объекта относительно произвольной прямой линии, причем не проходящей через начало координат. Используемый теперь подход позволяет достичь этого преобразованием, включающим пять последовательных операций:

§ перемещение объекта преобразования вдоль оси x или y таким образом, чтобы линия, относительно которой он отражается, прошла через начало координат;

§ поворот объекта относительно точки начала координат до совпадения линии, относительно которой он отражается, с одной из координатных осей;

§ симметричное отражение объекта относительно данной координатной оси;

§ обратный поворот объекта относительно точки начала координат (на тот же угол, что и во втором пункте, но в обратном направлении);

§ обратное перемещение объекта вдоль оси x или y (на то же расстояние, что и в первом пункте, но в обратном направлении).

В матричном виде полное преобразование, представляющее собой комбинацию пяти преобразований, можно записать так:

,

где – матрица перемещения, – матрица поворота вокруг начала координат, – матрица отражения относительно соответствующей координатной оси, и – матрицы, обратные матрицам соответственно и .

Приведем конкретный пример: симметричное отражение треугольника F (рис.2.11а), координатные векторы вершин которого представляются как , и , относительно прямой линии . Для того, чтобы линия прошла через точку начала координат, можно осуществить перемещение вдоль оси y на – 2 единицы; поворот относительно начала координат на – arctg 0,5 = – 26,57 ° приведет к тому, что линия совпадет с осью x; матрица отражения относительно оси x очевидна; обратный поворот и обратное перемещение осуществляются матрицами, обратными матрицам второго и первого преобразований. Композиция преобразований будет иметь вид:

;

реализуя полное преобразование, получим:

;

рис.2.11б, в, г, д иллюстрируют различные этапы промежуточных преобразований в случае последовательного их применения к исходной матрице, а рис.2.11е – конечный результат (который, вообще говоря, получен одной матричной операцией после расчета матрицы полного преобразования) – треугольник F*.

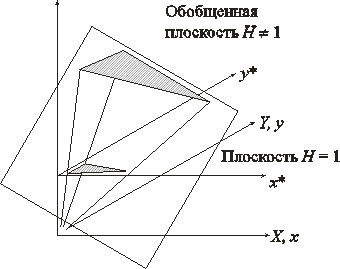
2.12. Проецирование в однородных координатах

Матрицу общего преобразования для трехмерных координатных векторов, используемых при двумерных преобразованиях, в общем виде можно представить так:

.

Ранее было установлено, как входящие в нее коэффициенты a, b, c, d, m и n влияют на соответствующие преобразования. Остальным трем коэффициентам в предыдущих разделах присваивались вполне определенные значения ( p = q = 0, s = 1), и они, по сути дела, не принимали участия в преобразованиях. Координатные векторы преобразованных точек всегда имели вид , т. е. число h (см. раздел 2.8) тождественно принимало единичное значение. Геометрически это можно трактовать как ограничение преобразований физической плоскостью h = 1 в трехмерном пространстве xyh. Вместе с тем, при других значениях коэффициентов p, q и s они также могут участвовать в преобразованиях.

Рассмотрим сначала, к какому эффекту приведут ненулевые значения коэффициентов p и q. Запишем следующее выражение:

;

данное преобразование привело к тому, что точка (x, y), которой изначально ставился в соответствие координатный вектор вида , преобразована в точку, которой ставится в соответствие координатный вектор вида , где x¢ = x, y¢ = y, ; с геометрической точки зрения полученный результат интерпретируется следующим образом: в трехмерном пространстве xyh конец P (рис.2.12) координатного вектора исходной точки принадлежит плоскости h = 1, а конец P¢ координатного вектора преобразованной точки – плоскости (причем в данном конкретном случае две другие компоненты однородных координат и соответствующего координатного вектора остаются неизменными).

Однако, как отмечалось ранее, в компьютерной графике используют векторы положения только вида . Поэтому, когда какое-либо преобразование приводит к результату с h ≠ 1 (и, кстати, с h ≠ 0), этот результат нормализуют, т. е. приводят к требуемому виду путем деления всех трех составляющих однородных координат на величину h. В рассматриваемой задаче окончательный результат преобразования будет иметь вид

;

геометрически такой же результат, а именно точку P* (рис.2.12), можно получить путем проецирования точки P¢, принадлежащей плоскости h ≠ 1, на плоскость h = 1 по лучу, соединяющему точку P¢ с началом координат.

Нетрудно заметить, что при h > 1 (как на рис.2.12) координаты x* и y* преобразованной точки пропорционально уменьшаются (в h раз) по сравнению теми же координатами исходной точки; при h 1 имеет место равномерное расширение, при 0 1 – равномерное сжатие, если 0 0, на положительной полуоси x, при условии, что x 0 положительной полуоси y, при y 0 – в первом квадранте координатной плоскости xy, при x = y 0, y 0 – во втором ее квадранте.

Двумерные преобразования в однородных координатах параллельные прямые

Преобразования переноса, масштабирования и поворота записываются в матричной форме в виде

,

,

.

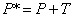
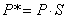
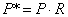
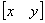
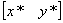
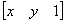
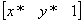
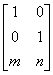
Очевидно, что перенос, в отличие от масштабирования и поворота, реализуется с помощью сложения. Это обусловлено тем, что вводить константы переноса внутрь структуры общей матрицы размером 2 ´ 2 не представляется возможным. Желательным является представление преобразований в единой форме – с помощью умножения матриц. Эту проблему можно решить за счет введения третьей компоненты в векторы точек и , т. е. представляя их в виде и . Матрица преобразования после этого становится матрицей размером 3 ´ 2:

.

Это необходимо, поскольку число столбцов в матрице, описывающей точку, должно равняться числу строк в матрице преобразования для выполнения операции умножения матриц. Таким образом,

,

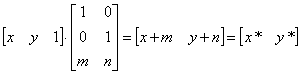
откуда следует, что константы т, п вызывают смещение х* и y* относительно х и у. Поскольку матрица 3 ´ 2 не является квадрат­ной, она не имеет обратной матрицы. Эту трудность можно обойти, дополнив матрицу преобразования до квадратной размером 3 ´ 3. Например,

.

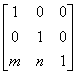
Заметим, что третья компонента векторов положения точек не изменяется при добавлении третьего столбца к матрице преобра­зования. Используя эту матрицу в соотношении, полу­чаем преобразованный вектор [х* у* 1]. Добавление третьего элемента к вектору положения и третьего столбца к матрице преобразования позволяет выполнить смещение вектора поло­жения. Третий элемент здесь можно рассматривать как дополни­тельную координату вектора положения. Итак, вектор положе­ния [х у 1] при воздействии на него матрицы 3 ´ 3 становится вектором положения в общем случае вида [X Y Н]. Представ­ленное преобразование было выполнено так, что

Преобразование, имеющее место в трехмерном пространстве, в нашем случае ограничено плоскостью, поскольку H = 1. Если, однако, третий столбец

матрицы преобразования Т размера 3 х 3 отличен от 0, то в результате матричного преобразования получим [х у 1] =[Х Y Н], где Н ¹ 1.

Плоскость, в которой теперь лежит преобразованный вектор положения, находится в трехмерном пространстве. Однако сейчас нас не интересует то, что происходит в трехмерном про­странстве.

Итак, найденные х* и у* получены с помощью пучка лучей, проходящих через на­чало координат. Результат пре­образований показан на рис. 3.3 .

Рис. 3.3. Геометрическое представление однородных координат

Из рассмотрения подобных треугольников видно, что

и .

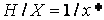
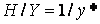
Рассматривая три компоненты, запишем это в виде

.

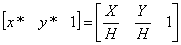
Представление двумерного вектора трехмерным или в общем случае n -мерного вектора (п + 1)-мерным называют однородным координатным воспроизведением. При однородном координат­ном воспроизведении n -мерного вектора оно выполняется в (п + 1)-мерном пространстве, и конечные результаты в n -мерном пространстве получают с помощью обратного преобразова­ния. Таким образом, двумерный вектор [х у] представляется трехкомпонентным вектором 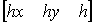. 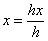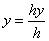Разделив компоненты вектора на однородную координату h, получим

и .

Не существует единственного однородного координатного пред­ставления точки в двумерном пространстве. Например, однород­ные координаты (12, 8, 4), (6, 4, 2) и (3, 2, 1) представляют исход­ную точку [3 2]. Для простоты вычислений выбираем [х у 1], чтобы представить непреобразованную точку в двумерных одно­родных координатах. Преобразование

в дополнительных координатах задается выражением в однород­ных координатах в виде

.

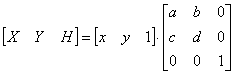
Выполнение указанных выше преобразований показывает, что Х = х*, Y = у*, а Н = 1. Равенство единице дополнительной координаты означает, что преобразованные однородные коор­динаты равны исходным координатам.

В общем случае Н ¹ 1, и преобразованные обычные коорди­наты получаются за счет нормализации однородных координат, т. е.

и .

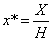
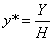
Геометрически все преобразования х и у происходят в пло­скости Н = 1 после нормализации преобразованных однород­ных координат.

Преимущество введения однородных координат проявляется при использовании матрицы преобразований общего вида по­рядка 3 ´ 3

,

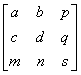
с помощью которой можно выполнять и другие преобразования, такие как смещение, операции изменения масштаба и сдвига, обусловленные матричными элементами а, b, с и d. Указанные операции рассмотрены ранее.

Чтобы показать воздействие третьего столбца матрицы преоб­разований 3 ´ 3, рассмотрим следующую операцию:

;

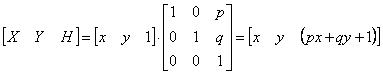
здесь Х = х, Y = у, а Н = рх + qy + 1. Переменная Н, ко­торая определяет плоскость, содержащую преобразованные точки, представленные в однородных координатах, теперь обра­зует уравнение плоскости в трехмерном пространстве.

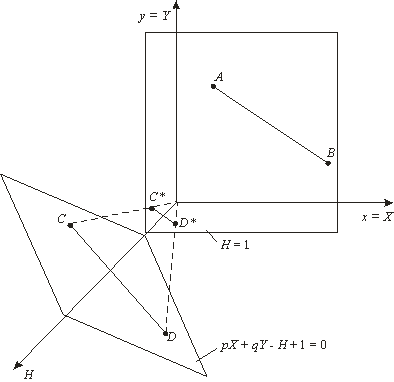
Это преоб­разование показано на рис. 3.4 , где линия АВ, лежащая в пло­скости ху, спроектирована на линию CD плоскости рХ + qY — Н + 1 = 0.

Рис. 3.4. Преобразование линии в однородных координатах

На рисунке величина р = q = 1.Выполним нормализацию для того, чтобы получить обыч­ные координаты:

,

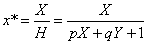
Полагая р = q = 1, для изображенных на рисунке точек А и В с координатами соответственно (1, 3) и (4, 1) получим

и .

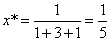
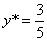
После преобразования А в С* и В в D* имеем

и .

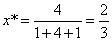
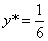
Однородные координаты для точек С* и D*, показанные на рисунке, соответственно равны

и .

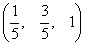
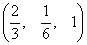
Результатом нормализации является перевод трехмерной линии CD в ее проекцию C * D * на плоскость Н = 1. Как показано на рисунке, центром проекции является начало координат.

Основная матрица преобразования размером 3 ´ 3 для дву­мерных однородных координат может быть подразделена на че­тыре части:

.

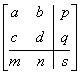
Как мы видим, а, b , с и d осуществляют изменение масштаба, сдвиг и вращение; т и п выполняют смещение, а р и q — полу­чение проекций. Оставшаяся часть матрицы, элемент s, произ­водит полное изменение масштаба. Чтобы показать это, рассмо­трим преобразование

Здесь Х = х, Y = у, а Н = s. Это дает х* = x / s и y * == y / s . В результате преобразования [х у 1 ] —> [ x / s y / s 1] имеет место однородное изменение масштаба вектора положения. При s 1 — уменьшение масштаба.

КООРДИНАТЫ И ПРЕОБРАЗОВАНИЯ

Описание, конструирование, манипулирование и представление геометрических объектов являются центральными работами в графических системах. Их поддержка в требуемом объеме за счет соответствующих математических методов, алгоритмов и программ оказывают существенное влияние на возможности и эффективность графической системы. В данном разделе будут рассмотрены математические методы для описания геометрических преобразований координат в двух, трех и четырехмерном случае, будут обсуждены некоторые вопросы эффективности, рассмотрены геометрические преобразования растровых картин.

Далее большими буквами X, Y, Z будут обозначаться обычные декартовые координаты, а маленькие буквы x, y, z будут использоваться для обозначения т.н. однородных координат.

0.1.1 Двумерные преобразования

Преобразование сдвига в плоском случае имеет вид:

Xn = X + Tx, Yn = Y + Ty,

(0.1.1)

или в векторной форме:

Pn = P + T,

(0.1.2)

где ¯ Pn = [Xn Yn] ¯ — ¯ вектор-строка преобразованных координат, где X,Y — исходные координаты точки,
Tx,Ty — величина сдвига по осям,
Xn,Yn — преобразованные координаты.
P = [X Y] — вектор-строка исходных координат,
Pn = [Xn Yn] — вектор-строка преобразованных координат,
T = [Tx Ty] — вектор-строка сдвига.

Преобразование масштабирования относительно начала координат имеет вид:

Xn = X ·Sx, Yn = Y ·Sy,

(0.1.3)

или в матричной форме:

Pn = P ·S,

(0.1.4)

где Sx, Sy — коэффициенты масштабирования по осям, а

S = [

Sx	0
0	Sy

] — матрица масштабирования.

Преобразование поворота относительно начала координат имеет вид:

Xn = X ·cos f — Y ·sin f , Yn = X ·sin f + Y ·cos f ,

(0.1.5)

или в матричной форме:

Pn = P ·R,

(0.1.6)

где f — угол поворота, а

R = [

cos f	sin f
-sin f	cos f

] — матрица поворота.

Столбцы и строки матрицы поворота представляют собой взаимно ортогональные единичные векторы. В самом деле квадраты длин векторов-строк равны единице:

cos f ·cos f +sin f ·sin f = 1 и

(-sin f ) ·(-sin f )+cos f ·cos f = 1,

а скалярное произведение векторов-строк есть

cos f ·(-sin f ) + sin f ·cos f = 0.

Так как скалярное произведение векторов A ·B = | A | · | B | ·cos y , где | A | — длина вектора A, | B | — длина вектора B, а y — наименьший положительный угол между ними, то из равенства 0 скалярного произведения двух векторов-строк длины 1 следует, что угол между ними равен 90 ° .

Аналогичное можно показать и для векторов-столбцов. Кроме того вектора-столбцы представляют собой такие единичные векторы, которые после выполнения преобразования, заданного этой матрицей, совпадут с осями. В самом деле, произведение первого столбца на матрицу есть

щ ы cos f -sin f щ ы · щ ъ ы cos f sin f -sin f cos f щ ъ ы = щ ы 1 0 щ ы ,

(0.1.7)

т.е. это единичный вектор вдоль оси X. Аналогично, произведение второго столбца на матрицу даст вектор [ 0 1 ]. Это позволяет сформировать матрицу, если известны результаты преобразования (см. пример в п. ).

0.1.2 Двумерные преобразования в однородных координатах

Как видно из (2), (4) и (6) двумерные преобразования имеют различный вид. Сдвиг реализуется сложением, а масштабирование и поворот — умножением. Это различие затрудняет формирование суммарного преобразования и устраняется использованием двумерных однородных координат точки, имеющих вид:

[ x y w ].

Здесь w — произвольный множитель не равный 0.

Двумерные декартовые координаты точки получаются из однородных делением на множитель w:

X = x / w, Y = y / w.

(0.1.8)

Однородные координаты можно представить как промасштабированные с коэффициентом w значения двумерных координат, расположенные в плоскости с Z = w.

В силу произвольности значения w в однородных координатах не существует единственного представления точки, заданной в декартовых координатах.

Преобразования сдвига, масштабирования и поворота в однородных координатах относительно центра координат все имеют одинаковую форму произведения вектора исходных координат на матрицу преобразования.

| | xn yn wn | | = щ ы x y w щ ы · | | | | | | 1 0 0 0 1 0 Tx Ty 1 щ ъ ъ ъ ъ ы .

(0.1.9)

| | xn yn wn | | = | | x y w | | · | | | | | | Sx 0 0 0 Sy 0 0 0 1 | | | | | | .

(0.1.10)

щ ы xn yn wn щ ы = щ ы x y w щ ы · щ ъ ъ ъ ъ ы cos f sin f 0 -sin f cos f 0 0 0 1 щ ъ ъ ъ ъ ы .

(0.1.11)

Как видно из (9) — (11), wn = w, а матрица преобразования для двумерных однородных координат в общем случае имеет вид:

щ ъ ъ ъ ъ ъ ъ ъ ы A B D E P Q L M S щ ъ ъ ъ ъ ъ ъ ъ ы ,

(0.1.12)

где элементы A, B, D и E определяют изменение масштаба, поворот и смещение, а L и M определяют сдвиг. Покажем, что элемент S определяет общее изменение масштаба, а элементы P и Q определяют проецирование.

Рассмотрим вначале для этого преобразование

щ ы xn yn h щ ы = щ ы x y 1 щ ы · щ ъ ъ ъ ъ ы 1 0 0 0 1 0 0 0 S щ ъ ъ ъ ъ ы .

Легко видеть, что xn = x, yn = y, h = S. Таким образом двумерные декартовые координаты преобразованной точки

Xn = xn / h = x / S, Yn = yn / h = y / S,

т.е. такое преобразование задает изменение масштаба вектора положения точки. При S 1 — увеличение.

Для уяснения смысла третьего столбца матрицы преобразований (12) выполним преобразование

щ ы xn yn h щ ы = щ ы x y 1 щ ы · щ ъ ъ ъ ъ ы 1 0 P 0 1 Q 0 0 1 щ ъ ъ ъ ъ ы = щ ы x y (Px+Qy+1) щ ы .

Здесь xn = x, yn = y, h = Px + Qy + 1, т.е. переменная h, которая определяет плоскость, содержащую преобразованные точки, представленные в однородных координатах, образует теперь уравнение плоскости в трехмерном пространстве:

h = Px + Qy + 1.

(0.1.13)

Получим результирующие двумерные декартовые координаты Xn, Yn для преобразованной точки

Xn = x Px + Qy + 1 , Yn = y Px + Qy + 1 .

Это соответствует вычислению их в плоскости Z = 1, т.е. проецированию из плоскости (13) в плоскость Z = 1. Легко показать, что центр проецирования находится в начале координат. Рассмотрим для этого параметрические уравнения прямой, проходящей через точки (X₀, Y₀, 1) и (X, Y, (MX+NY+1) ):

X(t) = X0 + (X-X0) ×t = x/h + (x — x/h) ×t Y(t) = Y0 + (Y-Y0) ×t = y/h + (y — y/h) ×t Z(t) = 1 + (MX+NY) ×t = 1 + (h — 1) ×t .

(0.1.14)

Из условия X(t) = X₀ = 0 находим t = 1/(1 — h), подставляя это значение t в выражения для Y(t) и Z(t), получим:

Y0 = y/h + (y — y/h)/(1-h) = y/h — y/h = 0.

Z0 = 1 + (h-1)/(1-h) = 0.

Итак, показано, что элементы P и Q матрицы (12) определяют проецирование с центром проекции в начале координат.

Кроме удобств, связанных с единообразным представлением преобразований, и, следовательно, с упрощением композиции преобразований, рассматриваемой в следующем пункте, однородные координаты дают возможность простого представления точек, имеющих в декартовой системе значение координаты, равное бесконечности.

Декартовые точки с бесконечными координатами

Рассмотрим в декартовой системе линию, проходящую через начало координат и точку (X,Y). Однородные координаты этой точки — (x,y,h) = (hX, hY, h), где h имеет произвольное значение. Предел отношения x/y при h стремящимся к 0 равен X/Y, но при этом декартовые координаты стремятся к бесконечности. Таким образом, точка с однородными координатами

(x, y, 0)

(0.1.15)

задает в декартовой системе точку на бесконечности для рассмотренной прямой. В частности, точка с однородными координатами (1, 0, 0) задает бесконечную точку на декартовой оси X, а точка с однородными координатами (0, 1, 0) задает бесконечную точку на декартовой оси Y.

Параллельные прямые

Покажем, что прямые, параллельные в декартовой системе координат, в однородных координатах имеют точку пересечения. Эта особенность далее будет использована при анализе перспективных преобразований.

Пусть две пересекающиеся прямые в декартовой системе координат заданы системой уравнений:

A1 ·X + B1 ·Y + C1 = 0 A2 ·X + B2 ·Y + C2 = 0.

(0.1.16)

Решая эту систему относительно X и Y, найдем координаты точки пересечения

X0 = C1 ·B2-C2 ·B1 A1 ·B2-A2 ·B1 .

Y0 = A1 ·C2-A2 ·C1 A1 ·B2-A2 ·B1 .

Запишем результат в однородных координатах

ц ч ш C1 ·B2-C2 ·B1 A1 ·B2-A2 ·B1 , A1 ·C2-A2 ·C1 A1 ·B2-A2 ·B1 , 1 ц ч ш .

В силу произвольности масштабного множителя, умножим значения координат на (A₁ ·B₂ — A₂ ·B₁)

(C1 ·B2-C2 ·B1, A1 ·C2-A2 ·C1, A1 ·B2-A2 ·B1).

Если прямые параллельны, то определитель системы (16) — (A₁ ·B₂-A₂ ·B₁) равен нулю. Учитывая это и обозначая x₀ = (C₁ ·B₂-C₂ ·B₁), y₀ = (A₁ ·C₂-A₂ ·C₁), получим координату пересечения параллельных прямых в однородной системе координат

( x0, y0, 0 ).

При этом точка пересечения лежит на прямой -y₀ ·x + x₀ ·y = 0 на бесконечности.

0.1.3 Композиция двумерных преобразований

Последовательное выполнение нескольких преобразований можно представить в виде единой матрицы суммарного преобразования. Умножение на единственную матрицу, естественно, выполняется быстрее, чем последовательное умножение на несколько матриц.

Рассмотрим сдвиг точки P₀ на расстояние (Tx₁, Ty₁) в точку P₁, а затем сдвинем точку P₁ на расстояние (Tx₂, Ty₂) в точку P₂. Обозначая через T₁ и T₂ матрицы сдвига, в соответствии с (9) получим:

P1 = P0 ·T1; P2 = P1 ·T2 = (P0 ·T1) ·T2 = P0 ·(T1 ·T2) = P0 ·T.

Понятно, что сдвиг аддитивен, т.е. последовательное выполнение двух сдвигов должно быть эквивалентно одному сдвигу на расстояние (Tx₁+Tx₂, Ty₁+Ty₂). Для доказательства этого рассмотрим произведение матриц сдвига T₁ и T₂, равное

T = щ ъ ъ ъ ъ ы 1 0 0 0 1 0 Tx1 Ty1 1 щ ъ ъ ъ ъ ы · щ ъ ъ ъ ъ ы 1 0 0 0 1 0 Tx2 Ty2 1 щ ъ ъ ъ ъ ы =

щ ъ ъ ъ ъ ы 1 0 0 0 1 0 Tx1+Tx2 Ty1+Ty2 1 щ ъ ъ ъ ъ ы .

Итак, получили, что результирующий сдвиг есть (Tx₁+Tx₂, Ty₁+Ty₂), т.е. суммарный сдвиг, вычисленный как произведение матриц, как и ожидалось, аддитивен.

Рассмотрим теперь последовательное выполнение масштабирований, первое с коэффициентами (Sx₁, Sy₁), второе с коэффициентами (Sx₂, Sy₂). Следует ожидать, что суммарное масштабирование будет мультипликативным. Обозначая через S₁ и S₂ матрицы масштабирования, в соответствии с (10) получим

P1 = P0 ·S1, P2 = P1 ·S2 = (P0 ·S1) ·S2 = P0 ·(S1 ·S2) = P0 ·S.

Найдем значения элементов матрицы S

S = щ ъ ъ ъ ъ ы Sx1 0 0 0 Sy1 0 0 0 1 щ ъ ъ ъ ъ ы · щ ъ ъ ъ ъ ы Sx2 0 0 0 Sy2 0 0 0 1 щ ъ ъ ъ ъ ы = щ ъ ъ ъ ъ ы Sx1 ·Sx2 0 0 0 Sy1 ·Sy2 0 0 0 1 щ ъ ъ ъ ъ ы .

Итак, получили, что результирующее масштабирование есть (Sx₁ ·Sx₂, Sy₁ ·Sy₂), т.е. суммарное масштабирование, вычисленное как произведение матриц, как и ожидалось, мультипликативно.

Аналогичным образом можно показать, что два последовательных поворота аддитивны.

Рассмотрим выполнение часто используемого поворота изображения на угол f относительно заданной точки P(X,Y). Это преобразование можно представить как перенос начала координат в точку (X,Y), поворот на угол f относительно начала координат и обратный перенос начала координат:

Pn = P ·T(-X,-Y) ·R( f ) ·T(X,Y).

С использованием преобразований в однородных координатах, суммарное преобразование будет иметь простой вид:

щ ъ ъ ъ ъ ы 1 0 0 0 1 0 -X -Y 1 щ ъ ъ ъ ъ ы · щ ъ ъ ъ ъ ы cos f sin f 0 -sin f cos f 0 0 0 1 щ ъ ъ ъ ъ ы · щ ъ ъ ъ ъ ы 1 0 0 0 1 0 X Y 1 щ ъ ъ ъ ъ ы .

0.1.4 Эффективность преобразований

Суммарная матрица двумерных преобразований в однородных координатах имеет вид:

щ ъ ъ ъ ъ ы A B 0 D E 0 L M 1 щ ъ ъ ъ ъ ы ,

где элементы A, B, D и E, отвечающие за изменение масштаба, поворот и смещение, — объединенная матрица масштабирования и поворота, а L и M определяют суммарный сдвиг.

Вычисление преобразованных однородных координат точки P с непосредственным использованием T в выражении P ·T требует 9 операций умножения и 6 операций сложения. Но так как третья однородная координата может быть выбрана равной 1, а третий столбец T содержит единственный ненулевой элемент, равный 1, то преобразование декартовых координат может быть представлено в виде:

Xn = X ·A + Y ·D + L, Yn = X ·B + Y ·E + M,

что требует уже только 4 операции умножения и 4 операции сложения, что существенно меньше. Таким образом, несмотря на то, что матрицы 3×3 удобны при вычислении суммарного преобразования, выполнение фактического преобразования координат следует производить с учетом реальной структуры матрицы преобразования.

0.1.5 Трехмерные координаты

Далее при рассмотрении трехмерных преобразований, в основном, используется общепринятая в векторной алгебре правая система координат (рис. а). При этом, если смотреть со стороны положительной полуоси в центр координат, то поворот на +90 ° (против часовой стрелке) переводит одну положительную ось в другую (направление движения расположенного вдоль оси и поворачивающегося против часовой стрелки правого винта и положительной полуоси совпадают). В некоторых, специально оговариваемых случаях, используется левая система координат (см. рис. б). В левой системе координат положительными будут повороты по часовой стрелке, если смотреть с положительного конца полуоси. В трехмерной машинной графике более удобной является левая система координат. Тогда если, например, поверхность экрана совмещена с плоскостью XY, то большим удалениям от наблюдателя соответствую точки с большим значением Z (см. рис. б).

Работа с однородными трехмерными координатами и матрицами преобразования (формирование и композциция) подобна таковой для двумерного случая, поэтому здесь будут рассмотрены только матрицы преобразований сдвига, масштабирования и поворота и пример конструирования матрицы преобразования по известному его результату.

Подобно тому как в двумерном случае точка в однородных координатах представляется трехмерным вектором [ x y w ], а матрицы преобразований имеют размер 3×3, для трехмерного случая точка представляется четырехмерным вектором [ x y z w ], где w не равно 0, а матрицы преобразований имеют размер 4×4. Если w не равно 1, то декартовые координаты точки (X,Y,Z) получаются из соотношения:

[ X Y Z 1 ] = [ (x/w) (y/w) (z/w) 1 ].

Преобразование в однородных координатах описывается соотношением

[ xn yn zn wn ] = [ x y z w ] ·T.

Матрица преобразования T в общем случае имеет вид

щ ъ ъ ъ ъ ъ ъ ъ ъ ъ ъ ы A B C D E F I J K P Q R L M N S щ ъ ъ ъ ъ ъ ъ ъ ъ ъ ъ ы .

Подматрица 3×3 определяет суммарные смещение, масштабирование и поворот. Подматрица-строка 1×3 — [ L M N ] задает сдвиг. Подматрица-столбец 3×1 — [ P Q R ] отвечает за преобразование в перспективе. Последний скалярный элемент — S определяет общее изменение масштаба.

В частности, матрица сдвига имеет вид:

T(Tx, Ty, Tz) = щ ъ ъ ъ ъ ъ ы 1 0 0 0 0 1 0 0 0 0 1 0 Tx Ty Tz 1 щ ъ ъ ъ ъ ъ ы .

Матрица обратного преобразования для сдвига получается путем смены знака у Tx, Ty и Tz.

Матрица масштабирования относительно центра координат имеет вид:

S(Sx, Sy, Sz) = щ ъ ъ ъ ъ ъ ы Sx 0 0 0 0 Sy 0 0 0 0 Sz 0 0 0 0 1 щ ъ ъ ъ ъ ъ ы .

Матрица обратного преобразования для масштабирования формируется при замене Sx, Sy и Sz на величины, обратные к ним.

Ранее рассмотренная для двумерного случая матрица поворота (11) является в то же время трехмерным поворотом вокруг оси Z. Так как при трехмерном повороте вокруг оси Z (поворот в плоскости XY) размеры вдоль оси Z неизменны, то все элементы третьей строки и третьего столбца равны 0, кроме диагонального, равного 1:

Rz( f z) = щ ъ ъ ъ ъ ъ ы cos f z sin f z 0 0 -sin f z cos f z 0 0 0 0 1 0 0 0 0 1 щ ъ ъ ъ ъ ъ ы .

При повороте вокруг оси X (в плоскости YZ) размеры вдоль оси X не меняются, поэтому все элементы первой строки и первого столбца равны 0, за исключением диагонального, равного 1:

Rx( f x) = щ ъ ъ ъ ъ ъ ы 1 0 0 0 0 cos f x sin f x 0 0 -sin f x cos f x 0 0 0 0 1 щ ъ ъ ъ ъ ъ ы .

При повороте вокруг оси Y (в плоскости XZ) размеры вдоль оси Y не меняются, поэтому все элементы второй строки и второго столбца равны 0, за исключением диагонального, равного 1:

Ry( f y) = щ ъ ъ ъ ъ ъ ы cos f y 0 -sin f y 0 0 1 0 0 sin f y 0 cos f y 0 0 0 0 1 щ ъ ъ ъ ъ ъ ы .

Столбцы и строки подматриц 3×3 матриц поворота Rx, Ry, Rz, аналогично двумерному случаю, представляют собой взаимно ортогональные единичные векторы. Легко убедиться, что суммарная матрица преобразования для произвольной последовательности поворотов вокруг осей X, Y и Z имеет вид:

R = щ ъ ъ ъ ъ ъ ы r1x r1y r1z 0 r2x r2y r2z 0 r3x r3y r3z 0 0 0 0 1 щ ъ ъ ъ ъ ъ ы

причем столбцы (и строки) представляют собой взаимно ортогональные единичные векторы. Более того, векторы-столбцы при повороте, задаваемом матрицей, совмещаются с соответствующими осями координат. Матрица, столбцы (или строки) которой представляют собой взаимно ортогональные векторы, называется ортогональной. Для любой ортогональной матрицы М обратная матрица совпадает с транспонированной. Это обеспечивает простоту вычисления обратного преобразования для поворота. Причем не надо фактически выполнять транспонирование, а достаточно просто поменять местами индексы строк и столбцов.

Взаимная ортогональность столбцов матрицы поворота и их совмещение с осями координат при преобразовании, задаваемом матрицей, позволяет легко сконструировать матрицу преобразования, если известны его результаты.

Пример формирования матрицы преобразования (из [])

Пусть заданы три точки P₁, P₂, P₃. Найти матрицу преобразования такого, что после преобразования вектор P₁P₂ будет направлен вдоль оси Z, а вектор P₁P₃ будет лежать в плоскости YZ.

Вначале надо сместить начало координат в точку P₁ с помощью преобразования

T(-x1, -y1, -z1).

Единичный вектор, который должен лечь вдоль оси Z

Rz = [r1z r2z r3z] = P1P2 / | P1P2 | .

Здесь | P₁P₂ | — длина вектора P₁P₂.

Вектор, перпендикулярный плоскости, построенной на векторах P₁P₂ и P₁P₃, должен быть направлен вдоль оси X, так как вектор P₁P₂ лежит вдоль оси Z, а вектор P₁P₃ лежит в плоскости YZ. Этот вектор задается векторным произведением

Rx = [r1x r2x r3x] = P1P2 ×P1P3 | P1P2 | · | P1P3 | .

Наконец, вдоль оси Y должен быть направлен вектор, перпендикулярный к векторам R_x и R_z:

Ry = [ r1y r2y r3y ] = Rz ×Rx.

Искомая матрица есть

M = T(-x1,-y1,-z1) · щ ъ ъ ъ ъ ъ ы r1x r1y r1z 0 r2x r2y r2z 0 r3x r3y r3z 0 0 0 0 1 щ ъ ъ ъ ъ ъ ы .

0.1.6 Проекции

При визуализации двумерных изображений достаточно задать окно видимости в системе координат пользователя и порт отображения на экране дисплея, в котором будет выдаваться изображение из окна. В этом случае достаточно провести отсечение изображения по окну и выполнить двумерные преобразования окно-порт. На рис. показан простой пример двумерных преобразований. Окном отсекается часть изображения домика и один улей (см. рис. слева). Отсеченное изображение передается в порт отображения дисплея с выполнением преобразований окно-порт (см. рис. справа). В данном (простом) случае выполняется только преобразование сдвига.

В случае же трехмерных изображений отсечение выполняется уже не по окну, а по объему видимости и затем выполняется проецирование в порт отображения, который в свою очередь может быть проекцией объема видимости. Модель процесса визуализации трехмерных изображений приведена на рис. .

Как уже отмечалось, проецирование в общем случае — отображение точек, заданных в системе координат размерностью N, в точки в системе с меньшей размерностью. При отображении трехмерных изображений на дисплей три измерения отображаются в два.

Проецирование выполняется с помощью прямолинейных проекторов (проецирующих лучей), идущих из центра проекции через каждую точку объекта до пересечения с картинной поверхностью (поверхностью проекции) . Далее рассматриваются только плоские проекции, при которых поверхность проекции — плоскость в трехмерном пространстве.

По расположению центра проекции относительно плоскости проекции различаются центральная и параллельные проекции.

При параллельной проекции центр проекции находится на бесконечном расстоянии от плоскости проекции. Проекторы представляют собой пучок параллельных лучей. В этом случае необходимо задавать направление проецирования и расположение плоскости проекции. По взаимному расположению проекторов, плоскости проекции и главных осей координат различаются ортогональные, прямоугольные аксонометрические и косоугольные аксонометрические проекции .

При ортогональной проекции проекторы перпендикулярны плоскости проекции, а плоскость проекции перпендикулярна главной оси. Т.е. проекторы параллельны главной оси.

При аксонометрической проекции имеется одна из двух перпендикулярностей:

при прямоугольной аксонометрической проекции проекторы перпендикулярны плоскости проекции, которая расположена под углом к главной оси;

при косоугольной аксонометрической проекции проекторы не перпендикулярны плоскости проекции, но плоскость проекции перпендикулярна к главной оси.

Изображение, полученное при параллельном проецировании, не достаточно реалистично, но передаются точные форма и размеры, хотя и возможно различное укорачивание для различных осей.

При центральной проекции расстояние от центра проекции до плоскости проецирования конечно, поэтому проекторы представляют собой пучок лучей, исходящих из центра проекции. В этом случае надо задавать расположение и центра проекции и плоскости проекции. Изображения на плоскости проекции имеют т.н. перспективные искажения, когда размер видимого изображения зависит от взаимного расположения центра проекции, объекта и плоскости проекции. Из-за перспективных искажений изображения, полученные центральной проекцией, более реалистичны, но нельзя точно передать форму и размеры. Различаются одно, двух и трехточечные центральные проекции в зависимости от того по скольким осям выполняется перспективное искажение. Иллюстрация центральной проекции приведена на рис. .

На рис. приведена классификация описанных выше плоских проекций.

Параллельные проекции

Вначале мы рассмотрим ортогональные проекции, используемые в техническом черчении, в регламентированной для него правосторонней системе координат, когда ось Z изображается вертикальной. Затем будут проиллюстрированы аксонометрические проекции также в правосторонней системе координат, но уже более близкой к машинной графике (ось Y вертикальна, ось X направлена горизонтально вправо, а ось Z — от экрана к наблюдателю). Наконец выведем матрицы преобразования в левосторонней системе координат, часто используемой в машинной графике, с вертикальной осью Y, осью X, направленной вправо и осью Z, направленной от наблюдателя.

Использование проекций в техническом черчении регламентируется стандартом ГОСТ 2.317-69. Наиболее широко, особенно, в САПР используются ортогональные проекции (виды). Вид — ортогональная проекция обращенной к наблюдателю видимой части поверхности предмета, расположенного между наблюдателем и плоскостью чертежа.

В техническом черчении за основные плоскости проекций принимают шесть граней куба (рис. ).

1. Вид спереди, главный вид, фронтальная проекция, (на заднюю грань V),
2. Вид сверху, план, горизонтальная проекция, (на нижнюю грань H),
3. Вид слева, профильная проекция, (на правую грань W),
4. Вид справа (на левую грань),
5. Вид снизу (на верхнюю грань),
6. Вид сзади (на переднюю грань).

Очевидно, что при ортогональной проекции не происходит изменения ни углов, ни масштабов.

При аксонометрическом проецировании (см. рис. 0.4) сохраняется параллельность прямых, а углы изменяются; измерение же расстояний вдоль каждой из координатных осей в общем случае должно выполняться со своим масштабным коэффициентом.

При изометрических проекциях укорачивания вдоль всех координатных осей одинаковы, поэтому можно производить измерения вдоль направлений осей с одним и тем же масштабом (отсюда и название изометрия). На рис. приведена (аксонометрическая прямоугольная) изометрическая проекция куба со стороной A. При этой проекции плоскость проецирования наклонена ко всем главным координатным осям под одинаковым углом. Стандартом регламентируется коэффициент сжатия, равный 0.82, а также расположение и взаимные углы главных координатных осей, равные 120 ° как это показано в левом верхнем углу рис. . Обычно сжатие не делается.

При диметрической проекции две из трех осей сокращены одинаково, т.е. из трех углов между нормалью к плоскости проекции и главными координатными осями два угла одинаковы. На рис. приведена (аксонометрическая прямоугольная) диметрическая проекция куба со стороной A. Там же показаны регламентируемые расположение осей и коэффициенты сжатия. Обычно вместо коэффициента сжатия 0.94 используется 1, а вместо 0.47 — 0.5.

В косоугольных проекциях плоскость проекции перпендикулярна главной координатной оси, а проекторы расположены под углом к ней. Таким образом, аксонометрические косоугольные проекции сочетают в себе свойства ортогональных и аксонометрических прямоугольных проекций.

Наиболее употребимы два вида косоугольной проекции — фронтальная (косоугольная) диметрия (проекция Kabinett — кабине) и горизонтальная (косоугольная) изометрия (проекция Kavalier — кавалье) или военная перспектива.

В случае фронтальной (косоугольной) диметрии при использовании правосторонней системы координат экрана плоскость проецирования перпендикулярна оси Z. Ось X направлена горизонтально вправо. Ось Z изображается по углом в 45 ° относительно горизонтального направления. Допускается угол наклона в 30 и 60 ° . При этом отрезки, перпендикулярные плоскости проекции, при проецирования сокращаются до 1/2 их истинной длины. На рис. приведена (аксонометрическая косоугольная) фронтальная диметрическая проекция куба со стороной A, там же показаны регламентируемые коэффициент сжатия, равный 0.5 и расположение осей.

В случае же (аксонометрической косоугольной) горизонтальной изометрии, как следует из названия, плоскость проецирования перпендикулярна оси Y а укорачивания по всем осям одинаковы и равны 1. Угол поворота изображения оси X относительно горизонтального направления составляет 30 ° . Допускается 45 и 60 ° при сохранении угла 90 ° между изображениями осей X и Z. Иллюстрация этого приведена на рис. .

Выведем выражения для матриц преобразования, используя теперь левостороннюю систему координат более естественную для машинной графики.

Простейшее параллельное проецирование — ортогональное выполняется на плоскость, перпендикулярную какой-либо оси, т.е. при направлении проецирования вдоль этой оси. В частности, проецирование в XY-плоскость, заданную соотношением Z = Z₀, выполняется следующим образом:

щ ы xn yn zn wn щ ы = щ ы x y z 1 щ ы · щ ъ ъ ъ ъ ъ ы 1 0 0 0 0 1 0 0 0 0 0 0 0 0 Z0 1 щ ъ ъ ъ ъ ъ ы .

Рассмотрим теперь косоугольное проецирование, при котором плоскость проецирования перпендикулярна главной оси, а проекторы составляют с плоскостью проецирования угол не равный 90 ° . Матрица для этого преобразования может быть найдена исходя из значений угла проецирования и координат преобразованной точки. На рис. показана косоугольная параллельная проекция единичного куба.

Из рисунка видно, что проектором, идущим из точки P₀ в P₁, точка P₀(0,0,1) проецируется в P₁(L·cos a , L·sin a , 0).

Теперь проектором, параллельным рассмотренному (рис. ), спроецируем некоторую точку (X,Y,Z) в точку (X_p,Y_p,Z_p).

Из подобия треугольников получаем:

(Xp-X)/Z = L·cos a Ю Xp = X + Z·L·cos a

(Yp-Y)/Z = L·sin a Ю Yp = Y + Z·L·sin a

Это соответствует следующему матричному выражению:

щ ы xp yp zp 1 щ ы = щ ы x y z 1 щ ы · щ ъ ъ ъ ъ ъ ы 1 1 0 0 0 0 0 0 L·cos a L·sin a 1 0 0 0 0 1 щ ъ ъ ъ ъ ъ ы .

Таким образом, матрица аксонометрической косоугольной проекции для случая проецирования в плоскость Z = 0, выполняет следующее:

вначале плоскости с заданной координатой Z₀ переносятся вдоль оси X на Z₀·L·cos a и вдоль оси Y на Z₀·L·sin a ,

затем производится проецирование в плоскость Z = 0.

Различные варианты параллельных проекций формируются из полученной подстановкой значений L и углов a и b (см. рис. 0.10). В частности, для фронтальной косоугольной диметрии L = 1/2, следовательно, угол b между проекторами и плоскостью проецирования равен arctan2 = 63.4 ° . Угол же a , равен 45 ° и допускается 30 и 60 ° , как это сказано выше. (Обратите внимание, что в этой системе координат плоскость фронтальной проекции — плоскость XY, в отличие от системы координат технического черчения, где фронтальная проекция, как это показано на рис. 0.5, формируется в плоскости XZ).

Центральная проекция

Наиболее реалистично трехмерные объекты выглядят в центральной проекции из-за перспективных искажений сцены. Центральные проекции параллельных прямых, не параллельных плоскости проекции будут сходиться в точке схода . В зависимости от числа точек схода, т.е. от числа координатных осей, которые пересекает плоскость проекции, различаются одно, двух и трехточечные центральные проекции. Иллюстрация одно-, двух- и трехточечной центральных проекций куба приведена на рис. .

Наиболее широко используется двухточечная центральная проекция.

Выведем матрицу, определяющую центральное проецирование для простого случая одноточечной проекции (рис. ), когда плоскость проекции перпендикулярна оси Z и расположена на расстоянии d от начала координат. (Здесь используется удобная для машинной графики левосторонняя система координат).

Начало отсчета находится в точке просмотра. Ясно, что изображения объектов, находящиеся между началом координат и плоскостью проекции увеличиваются, а изображения объектов, расположенных дальше от начала координат, чем плоскость проекции уменьшаются.

Из рис. 0.13 видно, что для координат (X1,Y1) точки P₁, полученной проецированием точки P₀(X,Y,Z) в плоскость Z = d (плоскость экрана) выполняются следующие соотношения:

X1 d = X Z , X1 d = X Z , X1 = X Z/d , Y1 = Y Z/d .

Такое преобразование может быть представлено матрицей 4×4

щ ы x1 y1 z1 w1 щ ы = щ ы x y z 1 щ ы · щ ъ ъ ъ ъ ъ ы 1 1 0 0 0 0 0 0 0 0 1 1/d 0 0 0 0 щ ъ ъ ъ ъ ъ ы =

щ ы x y z 1 щ ы ·Mц = щ ы x y z z/d щ ы .

Для перехода к декартовым координатам делим все на z/d и получаем:

[ X/(Z/d) Y/(Z/d) d 1 ].

Если же точка просмотра расположена в плоскости проекции, тогда центр проекции расположен в точке ( 0, 0, -d ). Рассматривая подобные треугольники, аналогично вышеописанному, можем получить:

X1 = X Z/d + 1 ; Y1 = Y Z/d + 1 .

Матрица преобразования в этом случае имеет вид:

M0 = щ ъ ъ ъ ъ ъ ы 1 0 0 0 0 1 0 0 0 0 0 1/d 0 0 0 1 щ ъ ъ ъ ъ ъ ы .

Матрица M₀ может быть представлена в виде:

M0 = T(0, 0, d) ·Mц ·T (0, 0, -d),

т.е. преобразование проецирования выполняется для этого случая путем переноса начала координат в центр проецирования, собственно проецирования и обратного сдвига начала координат.

0.1.7 Стереоизображения

Существенное повышение наглядности изображения достигается использованием псевдостереоизображений. В этом случае каждым глазом надо рассматривать отдельный перспективный вид. Оба таких вида отображаются на экран дисплея. Для их разделения могут использоваться:

· цветовое разделение, когда, например, изображение для левого глаза строится красным цветом, а для правого — синим и для просмотра используются цветные очки; недостаток этого способа состоит в том, что по сути дела можно формировать только простые каркасные изображения, но зато реализация проста и полностью используется пространственное разрешение дисплея;

· пространственное-временное разделение, когда, например, изображение для левого глаза строится в четных строках, а для правого — в нечетных и для просмотра используются электронные или электромеханические очки, перекрывающие или левый или правый глаз на время прорисовки нечетных, четных строк, соответственно; этот подход может быть реализован на дисплеях с чересстрочной разверткой, позволяет выводить достаточно динамические цветные полутоновые изображения, но с уменьшением вдвое разрешения по вертикали;

· временное разделение, когда для левого глаза используется одна страница видеопамяти, а для правого — вторая и происходит их переключение с достаточно большой частотой кадровой развертки; для перекрытия глаз также должны использоваться электронные или электромеханические очки; пространственное разрешение по строкам здесь не теряется.

Кроме этого, статические цветные псевдостереоизображения могут быть получены последовательным фотографированием изображений для левого и правого глаз с последующим просмотром через стереоскоп.

Используя результаты, полученные в предыдущем пункте, легко сконструировать матрицы преобразований для получения стереопроекций для левого и правого глаз.

0.1.8 Геометрические преобразования растровых картин

Также как и для векторных изображений в двумерном случае, для растровых картин могут в общем случае требоваться преобразования сдвига, масштабирования и поворота. В связи с существенно дискретным характером изображения при выполнении этих преобразований имеется ряд особенностей.

Преобразование сдвига реализуется наиболее просто и заключается в переписывании части изображения (bitblt — операции Bit Block Transfer). При этом возможно исполнение некоторых операций над старым и новым пикселами с одинаковыми координатами.

Наиболее употребимыми являются:

· замена — новый пиксел просто заменяет старый,

· исключающее ИЛИ — в видеопамять заносится результат операции XOR над старым и новым кодами пикселов. Эта операция обычно используется дважды — вначале для занесения некоторого изображения, например, перекрестия и повторного его занесения для восстановления исходной картины.

Кроме этого, для реализации техники «акварель», т.е. техники работы с прозрачными цветами, в видеопамять заносится результат цветовой интерполяции между старым и новым оттенками пикселов. Эта операция всегда точно реализуема в полноцветных дисплеях, хранящих значения R, G и B в каждом пикселе. В дисплеях с таблицей цветности возможно получение не совсем правильных результатов.

Преобразование масштабирования

Принято различать два типа масштабирования:
· целочисленное — zoom,

· произвольное, когда коэффициент масштабирования не обязательно целое число, — transfocation.

Наиболее просто реализуется целочисленное масштабирование. При увеличении в K раз каждый пиксел в строке дублируется К раз и полученная строка дублируется К раз. При уменьшении в K раз из каждой группы в K строк выбирается одна строка и в ней из каждой группы в K пикселов берется один пиксел в качестве результата. Не целочисленное масштабирование требует нерегулярного дублирования при увеличении и выбрасывания при уменьшении. Для отсутствия «дырок» в результирующем изображении при любых преобразованиях растровых картин следует для очередного пиксела результирующего изображения определить соответствующий (соответствующие) пикселы исходного изображения, вычислить значение пиксела и занести его.

Рассмотрим нецелочисленное уменьшение, т.е. перепись из большего массива в меньший (увеличение строится похожим образом).

Алгоритм ясен из следующей программы:

Понятно, что такой алгоритм требует точной вещественной арифметики, версия алгоритма с целочисленной арифметикой имеет вид:

Внутренняя часть цикла при записи на ассемблере существенно упрощается, если использовать то, что для обычных 16-ти разрядных ЭВМ при переполнении происходит смена знака.

Преобразование поворота

Определенные проблемы, связанные с дискретных характером изображения, возникают и при повороте растровой картины на угол не кратный 90 ° . Здесь возможны два подхода:

Сканируются строки исходной картины при этом вычисляются новые значения координат пикселов для результирующей картины. Ясно что отсутствие дырок на результирующем изображении может быть обеспечено только при использовании вещественной арифметики, кроме этого возможно повторное занесение пикселов.

Сканируются строки результирующей картины и по координатам очередного пиксела определяются координаты пиксела из исходного изображения. Этот подход гарантирует отсутствие дырок, кроме того исключает повторное занесение пикселов.

🎥 Видео