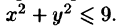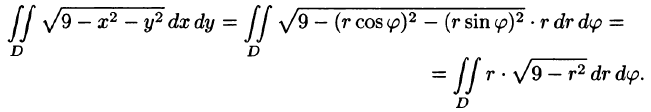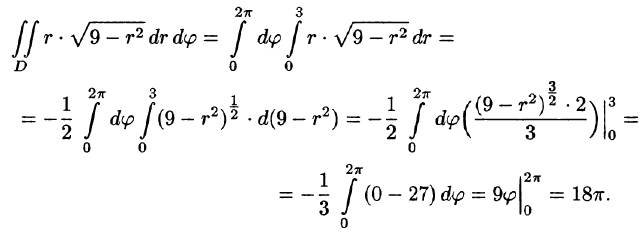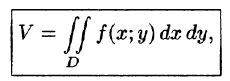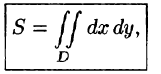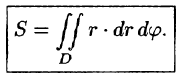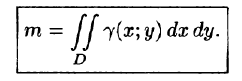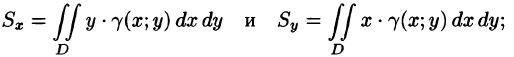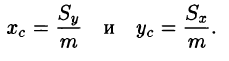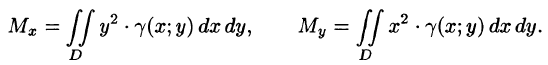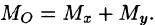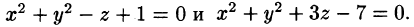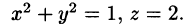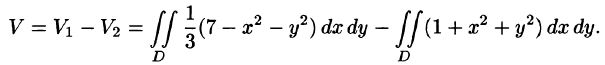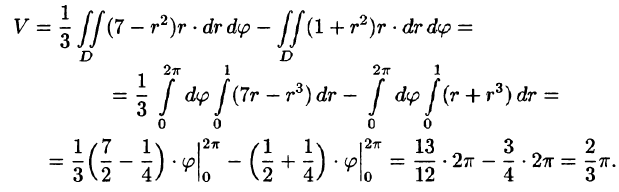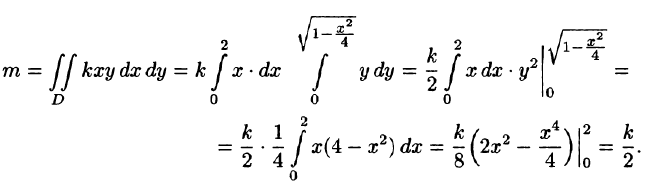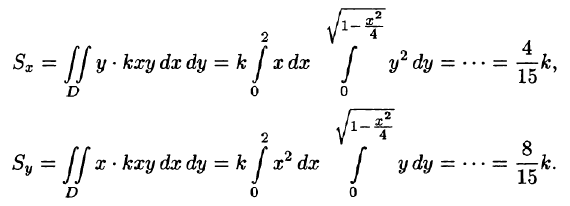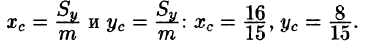- Что значит вычислить двойной интеграл в полярных координатах?
- Пределы интегрирования в повторных интегралах
- Случай первый
- Случай второй
- Случай третий
- Случай четвёртый
- Решения двойных интегралов в полярных координатах: примеры
- Двойной интеграл с примерами решения и образцами выполнения
- Геометрический и физический смысл двойного интеграла
- Масса плоской пластинки
- Основные свойства двойного интеграла
- Вычисление двойного интеграла в декартовых координатах
- Вычисление двойного интеграла в полярных координатах
- Приложения двойного интеграла
- Объем тела
- Площадь плоской фигуры
- Масса плоской фигуры
- Статические моменты и координаты центра тяжести плоской фигуры
- Моменты инерции плоской фигуры
- Двойной интеграл
- Вычисление двойного интеграла в полярной системе координат Текст научной статьи по специальности « Математика»
- Аннотация научной статьи по математике, автор научной работы — Махсуд Тулқин Ўғли Усмонов
- Похожие темы научных работ по математике , автор научной работы — Махсуд Тулқин Ўғли Усмонов
- Текст научной работы на тему «Вычисление двойного интеграла в полярной системе координат»
- 📹 Видео
Видео:Двойной интеграл / Как находить двойной интеграл через повторный (двукратный) / Два способаСкачать
Что значит вычислить двойной интеграл в полярных координатах?
Если область интегрирования представляет собой окружность или часть окружности, двойной интеграл проще вычислить не в декартовых прямоугольных координатах, а в полярных координатах. В этом случае подынтегральная функция выражается как функция полярных переменных r и φ с использованием соотношений между полярными и декартовыми координатами x = rcosφ и y = rsinφ :

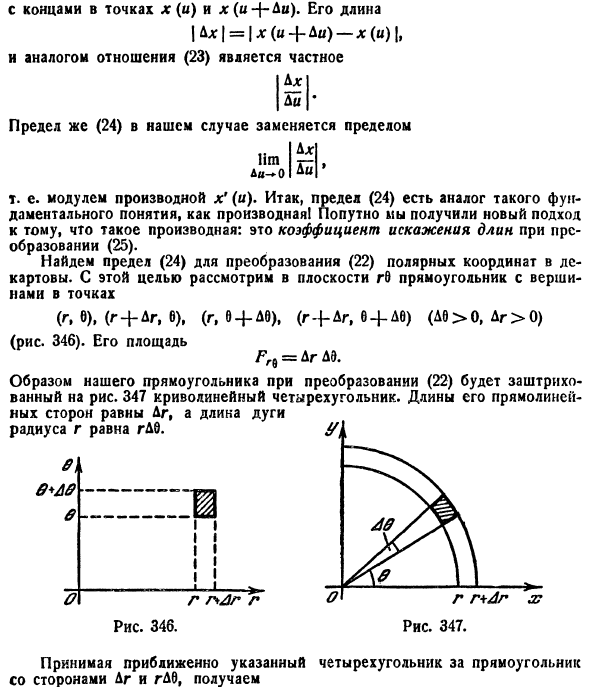
Что представляет собой элемент площади dxdy , выраженный в полярных координатах? Для ответ на этот вопрос разделим область интегрирования D на участки линиями окружности r = const и лучами φ = const . Рассмотрим один частичный участок (заштрихованный на рисунке), который ограничивают лучи, образующие с полярной осью углы φ и φ + dφ и линии окружности с радиусом r и r + dr . Этот криволинейный четырёхугольник можем приближенно считать прямоугольником с длиной боковой стороны dr и длиной основания rdφ . Поэтому элемент площади в полярных координатах выражается следующим образом:
а двойной интеграл в полярных координатах записывается так:

Чтобы вычислить двойной интеграл в полярных координатах, его нужно выразить через повторные интегралы, так же, как и «обычный» двойной интеграл в декартовых прямоугольных координатах. В полярных координатах внешний интеграл всегда интегрируется по углу φ , а внутренний — по радиусу r .
Вычислить двойной интеграл в полярных координатах — значит, как и в декартовых прямоугольных координатах, найти число, равное площади упомянутой фигуры D .
Видео:Двойной интеграл в полярных координатахСкачать

Пределы интегрирования в повторных интегралах
При переходе от двойного интеграла в полярных координатах к повторным интегралам расстановку пределов интегрирования могут облегчить следующие закономерности.
Случай первый
Полюс O является внутренней точкой области интегрирования D , область ограничена линией r = r(φ) .
Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны 0 и 2π , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай второй
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , но не является угловой точкой.
Через полюс O проведём касательную. Пусть касательная образует с полярной осью угол α . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и π + α , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай третий
Полюс O находится на границе области интегрирования D , ограниченного линией r = r(φ) , и является угловой точкой.
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — 0 и r(φ) . Переход к повторным интегралам осуществляется следующим образом:

Случай четвёртый
Полюс O находится вне области интегрирования D .
Из полюса O проведём лучи, которые будут ограничивать область D . Пусть эти лучи образуют с полярной осью углы α и β , а область D ограничивают линии r = r 1 (φ) и r = r 2 (φ) . Тогда соответственно нижний и верхний пределы интегрирования внешнего интеграла равны α и β , а внутреннего интеграла — r 1 (φ) и r 2 (φ) . Переход к повторным интегралам осуществляется следующим образом:

Видео:Вычислить двойной интеграл, перейдя к полярным координатамСкачать

Решения двойных интегралов в полярных координатах: примеры
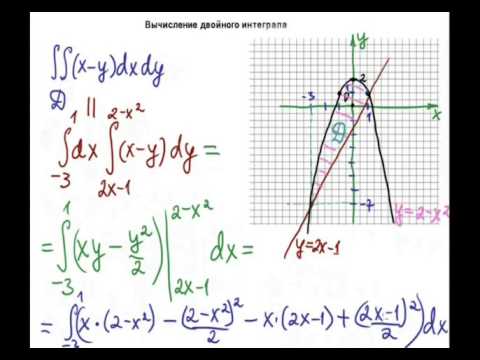
Пример 1. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 


Решение. Строим на чертеже область интегрирования. Видим, что этот пример относится к третьему случаю из вышеописанных четырёх случаев расположения области интегрирования.
Выразим подынтегральную функцию как функцию полярных переменных:

Данные в условии линии, ограничивающие D , приводим к полярным координатам:
Переходим от двойного интеграла к повторному, учитывая пределы интегрирования, верные в третьем случае:

Вычисляем интеграл (так как повторные интегралы независимы друг от друга, каждый из них вычисляем отдельно и результаты перемножаем):
Пример 2. В повторном интеграле
перейти к полярной системе координат.
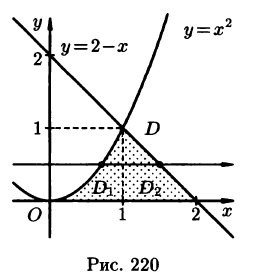
Решение. В повторном интеграле переменная x изменяется от -1 до 1, а переменная y — от параболы x² до 1. Таким образом, область интегрирования снизу ограничена параболой y = x² , а сверху — прямой y = 1 . Область интегирования изображена на следующем чертеже.
При переходе к полярным координатам область интегрирования нужно разделить на три части. Значит, данный повторный интеграл должен быть вычислен как сумма трёх интегралов. В первой области полярный радиус меняется от 0 до параболы, во второй области — от 0 до прямой y = 1 , в третьей области — от 0 до параболы. Точки пересечения прямой y = 1 и параболы: (1; 1) и (−1; 1) . В первой точке полярный угол составляет 




Запишем линии, ограничивающие область интегрирования в полярной системе координат. Найдём уравнение прямой y = 1 : 

Теперь у нас есть всё, чтобы от данного повторного интеграла перейти к полярным координатам:
Пример 3. Вычислить в полярных координатах двойной интеграл

где область D ограничена линией окружности 
Решение. Строим на чертеже область интегрирования.
Область интегрирования ограничивает линия окружности с центром в точке (a; 0) и радиусом a . В этом легко убедиться, преобразовав её уравнение следующим образом:

Линия окружности 




Напишем подынтегральную функцию в полярных координатах:

Теперь можем перейти в данном двойном интеграле к полярным координатам:
Наконец, находим двойной интеграл в полярных координатах:
В полученном выражении второе слагаемое равно нулю, так как и sinπ , и sin(−π) равны нулю. Продолжая, получаем:
Пример 4. Вычислить плоской фигуры, которую ограничивают линии 



Решение. Построим заданную фигуру на следующем рисунке.
Так как фигура является частью круга, её площадь проще вычислить в полярных координатах. Данные уравнения линий перепишем в полярных координатах:
Таким образом, у нас есть всё, чтобы записать площадь фигуры в виде двойного интеграл в полярных координатах, перейти к повторному интегралу и вычислить его:
Пример 5. Вычислить в полярных координатах двойной интеграл

где область D ограничена линиями 

Решение. Преобразуем данные уравнения линий, чтобы было проще построить чертёж:

Строим на чертеже область интегрирования.
В данных уравнениях линий перейдём к полярным координатам:

В данном двойном интеграле перейдём к полярным координатам, затем к повторным интегралам и вычислим интеграл:
Видео:Математический анализ, 41 урок, Вычисление двойных интеграловСкачать

Двойной интеграл с примерами решения и образцами выполнения
Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.
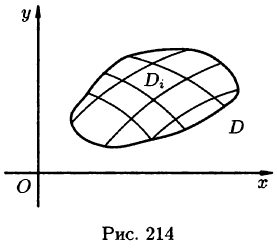
Пусть в замкнутой облас
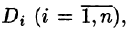

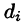
В каждой области 
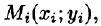
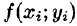

Эта сумма называется интегральной суммой функции f(x; у) в области D.
Рассмотрим предел интегральной суммы (53.1), когда п стремится к бесконечности таким образом, что 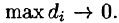
Таким образом, двойной интеграл определяется равенством
В этом случае функция f(x;y) называется интегрируемой в области D; D — область интегрирования; х и у — переменные интегрирования; dx dy (или dS) — элемент площади.
Для всякой ли функции f(x; у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.
Теорема:
Достаточное условие интегрируемости функции. Если функция z = f(x;y) непрерывна в замкнутой области D, то она интегрируема в этой области.
Замечания:
- Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.
- Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллельными координатным осям (см. рис. 215). При этом
равенство (53.2) можно записать в виде
Видео:Математика без ху!ни. Двойные интегралы. Часть1. Как вычислять.Скачать

Геометрический и физический смысл двойного интеграла
Рассмотрим две задачи, приводящие к двойному интегралу. Объем цилиндрического тела
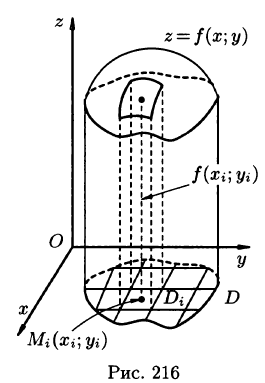
Рассмотрим тело, ограниченное сверху поверхностью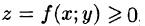

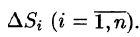

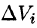
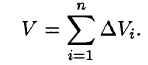
Возьмем на каждой площадке Di произвольную точку 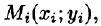

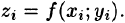
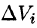
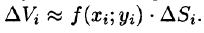
Это равенство тем точнее, чем больше число п и чем меньше размеры «элементарных областей» 

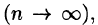
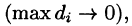
или, согласно равенству (53.2),
Итак, величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. В этом состоит геометрический смысл двойного интеграла.
Масса плоской пластинки
Требуется найти массу m плоской пластинки D. зная, что ее поверхностная плотность 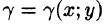
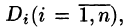


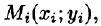
Если области D, достаточно малы, то плотность в каждой точке 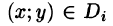
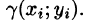

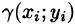
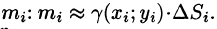
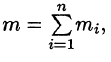
Точное значение массы получим как предел суммы (53.5) при условии
или, согласно равенству (53.2),
Итак, двойной интеграл от функции 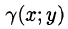
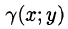
Видео:Математика без ху!ни. Двойной интеграл, вычисление двумя способами.Скачать
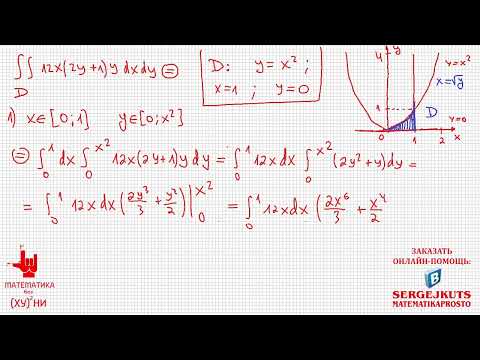
Основные свойства двойного интеграла
Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. § 35). Аналогичны и свойства этих интегралов и их доказательства (см. § 38). Поэтому перечислим основные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.
3.Если область D разбить линией на две области 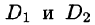
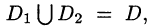
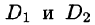
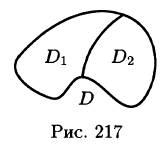
4.Если в области D имеет место неравенство 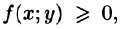
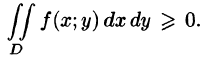
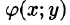
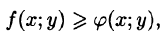
6.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой 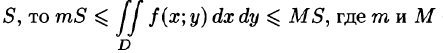
7.Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка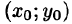
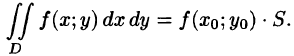
называют средним значением функции f(x; у) в области D.
Видео:Вычислить двойной интеграл по области, ограниченной линиями ∫∫(5x+y)dxdy D: y=x^3, y=0, x=3.Скачать

Вычисление двойного интеграла в декартовых координатах
Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.
Пусть требуется вычислить двойной интеграл 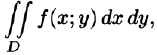
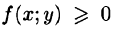
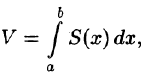
где S(x) — площадь сечения плоскостью, перпендикулярной оси Ох, а х = а, х = b — уравнения плоскостей, ограничивающих данное тело.
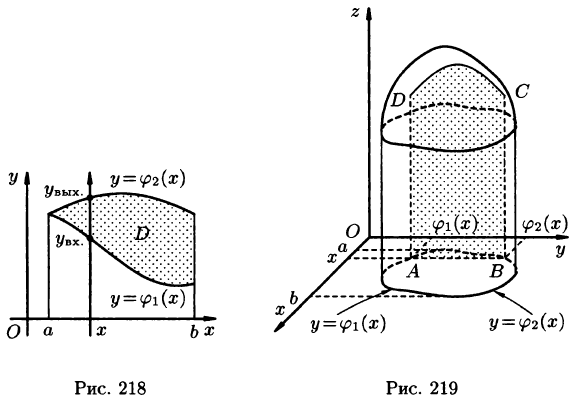
Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми x = a и x = b и кривыми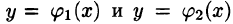
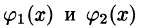
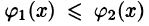
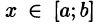
Построим сечение цилиндрического тела плоскостью, перпендикулярной оси
В сечении получим криволинейную трапецию ABCD, ограниченную линиями
Площадь S(x) этой трапеции находим с помощью определенного интеграла
Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найден так:
С другой стороны, в п. 53.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции 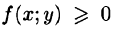
Это равенство обычно записывается в виде
Формула (53.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (53.7) называют двукратным (или повторным) интегралом от функции f(x;y) по области D. При этом 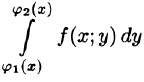
Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.
Если же область D ограничена прямыми 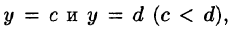
для всех 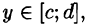
Здесь, при вычислении внутреннего интеграла, считаем у постоянным.
Замечания:
- Формулы (53.7) и (53.8) справедливы и в случае, когда
- Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (53.7), так и по формуле (53.8).
- Если область D не является правильной ни «по x», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении осиОх или оси Оу.
- Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.
Пример:
Вычислить 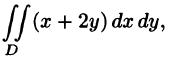
Решение:
На рисунке 220 изображена область интегрирования D. Она правильная в направлении оси Ох. Для вычисления данного двойного интеграла воспользуемся формулой (53.8):
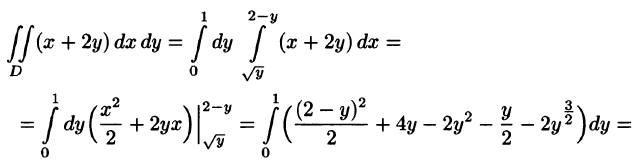
Отметим, что для вычисления данного двойного интеграла можно воспользоваться формулой (53.7). Но для этого область D следует разбить на две области: 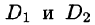
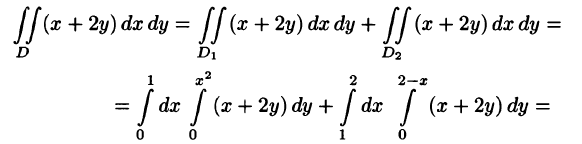
Ответ, разумеется, один и тот же.
Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Вычисление двойного интеграла в полярных координатах
Для упрощения вычисления двойного интеграла часто применяют метод подстановки (как это делалось и при вычислении определенного интеграла), т. е. вводят новые переменные под знаком двойного интеграла.
Определим преобразование независимых переменных х и у (замену переменных) как
Если функции (53.9) имеют в некоторой области D* плоскости Ouv непрерывные частные производные первого порядка и отличный от нуля определитель
а функция f(х; у) непрерывна в области D, то справедлива формула замены переменных в двойном интеграле:
Функциональный определитель (53.10) называется определителем Якоби или якобианом (Г. Якоби — немецкий математик). Доказательство формулы (53.11) не приводим.
Рассмотрим частный случай замены переменных, часто используемый при вычислении двойного интеграла, а именно замену декартовых координат х и у полярными координатами
В качестве инь возьмем полярные координаты 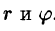
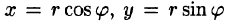
Правые части в этих равенствах — непрерывно дифференцируемые функции. Якобиан преобразования определяется из (53.10) как
Формула замены переменных (53.11) принимает вид:
где D* — область в полярной системе координат, соответствующая области D в декартовой системе координат.
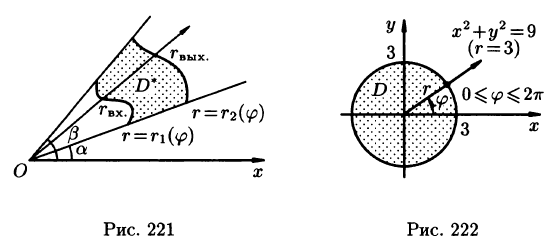
Для вычисления двойного интеграла в полярных координатах применяют то же правило сведения его к двукратному интегралу. Так, если
область D* имеет вид, изображенный на рисунке 221 (ограничена лучами 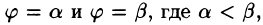
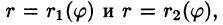
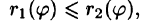
Внутренний интеграл берется при постоянном
Замечания:
- Переход к полярным координатам полезен, когда подынтегральная функция имеет вид
область Dесть круг, кольцо или часть таковых.
- На практике переход к полярным координатам осуществляется путем замены
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
(исследуя закон изменения
точки
при ее отождествлении с точкой (х; у) области D).
Пример:
Вычислить 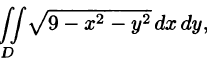
Решение: Применив формулу (53.12), перейдем к полярным координатам:
Область D в полярной системе координат определяется неравенствами (см. рис. 222) 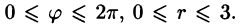
Видео:Математика без ху!ни. Двойные интегралы. Часть2.Скачать

Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
где z = f(x;y) — уравнение поверхности, ограничивающей тело сверху.
Площадь плоской фигуры
Если положить в формуле (53.4) f(x;y) = 1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой Н = 1. Объем такого цилиндра, как известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:
или, в полярных координатах,
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки D с переменной плотностью 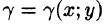
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей Ох и Оу (см. п. 41.6) могут быть вычислены по формулам
а координаты центра масс фигуры по формулам
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на квадрат расстояния d точки до оси, т. е. 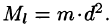
Момент инерции фигуры относительно начала координат — по формуле
Замечание:
Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример:
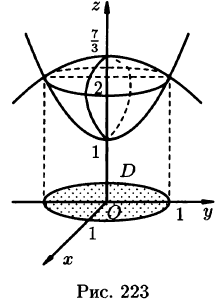
Найти объем тела, ограниченного поверхностями
Решение: Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
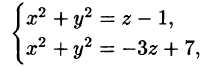
находим уравнение линии их пересечения:
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 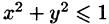
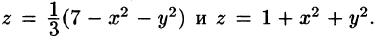
Переходя к полярным координатам, находим:
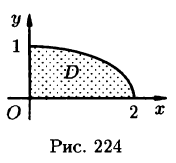
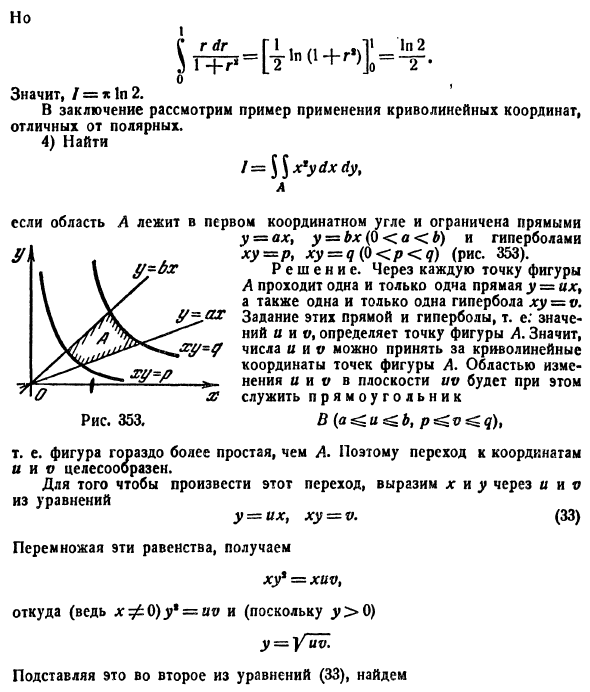
Пример:
Найти массу, статические моменты 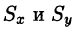
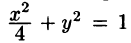
Решение: По формуле (53.6) находим массу пластинки. По условию, 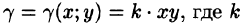
Находим статические моменты пластинки:
Находим координаты центра тяжести пластинки, используя формулы
Видео:Вычисление двойного интегралаСкачать
Двойной интеграл






























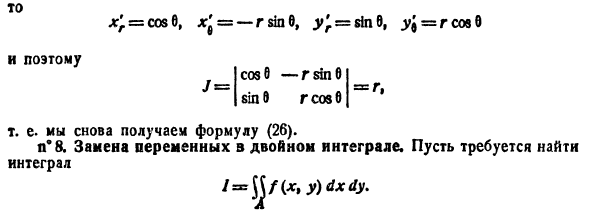

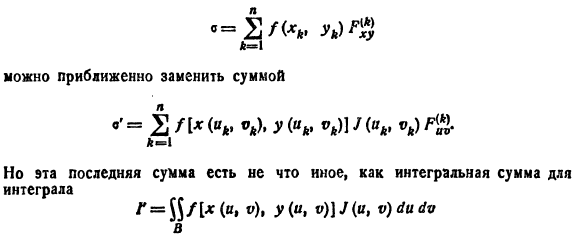




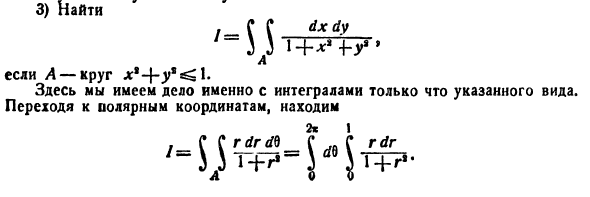




Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Изменение порядка интегрирования в повторном интегралеСкачать

Вычисление двойного интеграла в полярной системе координат Текст научной статьи по специальности « Математика»
Видео:Вычислить двойной интегралСкачать

Аннотация научной статьи по математике, автор научной работы — Махсуд Тулқин Ўғли Усмонов
В данной статье рассмотрим более простой и распространённый случай, когда подынтегральная функция двух переменных и двойной интеграл численно равен площади области интегрирования. Разберём алгоритм решения на демо-задаче.
Видео:Семинар 4. Двойной интеграл.Скачать

Похожие темы научных работ по математике , автор научной работы — Махсуд Тулқин Ўғли Усмонов
Видео:Двойной интеграл / Как находить двойной интегралСкачать

Текст научной работы на тему «Вычисление двойного интеграла в полярной системе координат»
Вычисление двойного интеграла в полярной системе
Махсуд Тулкин угли Усмонов maqsudu32@gmail .com Ташкентский университет информационных технологий
Аннотация: В данной статье рассмотрим более простой и распространённый случай, когда подынтегральная функция двух переменных и двойной интеграл численно равен площади области интегрирования. Разберём алгоритм решения на демо-задаче.
Ключевые слова: двойной интеграл в полярной системе координат, двойной интеграл.
Calculation of the double integral in the polar coordinate
Mahsud Tulgin oglu Usmonov maqsudu32@gmail.com Tashkent University of Information Technologies
Abstract: In this article, we will consider a simpler and more common case when the integrand of two variables and the double integral is numerically equal to the area of the region of integration. Let’s analyze the algorithm for solving the demo problem. Keywords: double integral in a polar coordinate system, double integral.
Вычислить площадь плоской фигуры, ограниченную линиями
х +у -2,у = 0,х = 0(х>0) с ПОМОщЬЮ двойного интеграла, используя полярную систему координат
Решение: Выполняем чертёж области D в прямоугольной системе координат. Линейное неравенство определяет правую полуплоскость,
включая ось а уравнение х очевидно, задаёт какую-то
линию 2-го порядка. Чтобы выяснить, какую именно — выделим полный квадрат:
окружность единичного радиуса с центром в точке Таким образом, требуется вычислить площадь половинки круга:
Перейдём к повторным интегралам:
S = || dxdy = || rdrd
Остальное — дело техники: 1)
задаёт площадь области
Прикинув по чертежу количество клеточек, приходим к выводу, что полученный результат вполне и вполне правдоподобен.
Вычислить двойной интеграл D
Решение: определённый интеграл s интегрирования.
В чём заключается особенность этого задания? Прежде всего, бросается в глаза, что область «дэ» ограничена единственной кривой, и по характерным признакам — это какая-то алгебраическая линия 4-го порядка. Основная проблема у нас с чертежом. Конечно, можно погрузиться в справочники, но на это нет ни времени, ни особого желания. Поэтому мы попытаемся ограничиться общим анализом и обойтись совсем без чертежа.
Можно ли обойтись без чертежа?
Если условие задачи его не требует — то можно. Правда, область интегрирования всё равно придётся представить мысленно.
Поскольку область интегрирования, как правило, ограничена, то уравнение
х = а (х -3у ) зада£Х либо единственную замкнутую кривую, либо несколько ограниченных областей — что-то наподобие лепестков полярной розы. Ситуацию помогла бы прояснить область определения функции, но её нахождение тоже затруднено ввиду навороченности уравнения.
Что делать? Подумать о возможности использования полярной системы координат. Причём подумать самостоятельно — условие нам совершенно не намекает на способ решения. Поскольку в уравнении присутствуют знакомые «икс квадрат» и «игрек квадрат», то применение полярных координат действительно выглядит перспективно. По формулам перехода х= г eos q>, у = г sin 0, косинус в знаменателе — в чётной степени:
Теперь займёмся областью определения. Поскольку тригонометрические функции периодичны, то нас интересует промежуток или, что то же
Знаменатель не может равняться нулю, поэтому 2 2 .
Кроме того, подкоренное выражение должно быть неотрицательным:
cos #?-3sin £?>0 сведём данное условие к простейшему тригонометрическому неравенству, применив формулы понижения степени:
2 _ . J l+cos2#? _ (1 — cos 2 =—3- —— = — + — cos2#?- — + — cos2#?= 2cos2
Я неоднократно ратовал за графическое решение подобных неравенств, но раз уж решили обойтись без чертежей, давайте вытащим из школьного учебника известную формулу. Решением неравенства где является
следующее множество промежутков:
— arccos d + 2тк Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
1. Kiselev, Andrey Petrovich // Great Soviet Encyclopedia: [in 30 volumes] / Ch. ed. A.M. Prokhorov. — 3rd ed. — M.: Soviet Encyclopedia, 1969-1978.
2. Andronov I.K., A.P. Kiselev. [Obituary], «Mathematics in School», 1941, no.
3. Margulis A. Ya., Andrey Petrovich Kiselev, «Mathematics at school», 1948,
4. Depman I. Ya., History of arithmetic, M., 1959.
5. Morgulis A. Ya., Trostnikov V. Legislator of school mathematics // Science and life. 1968. No. 1
📹 Видео
Объем через двойной интегралСкачать
Математический анализ, 40 урок, Двойные интегралы и их свойстваСкачать

Математический анализ, 43 урок, Приложения двойных интеграловСкачать

Вычислить двойной интеграл по областиСкачать






















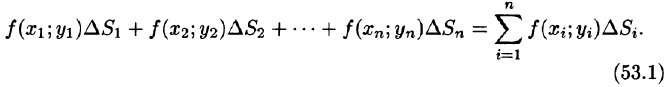
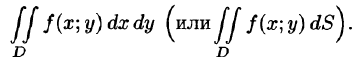
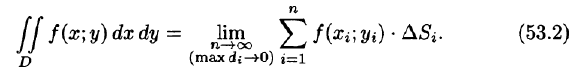
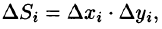 равенство (53.2) можно записать в виде
равенство (53.2) можно записать в виде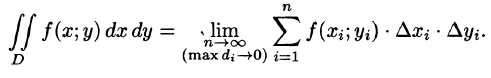
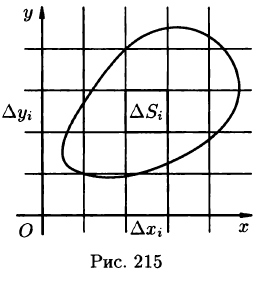

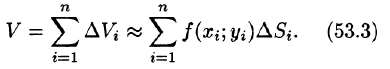
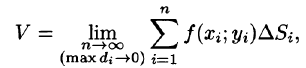
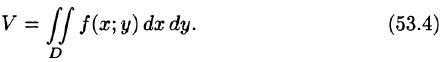
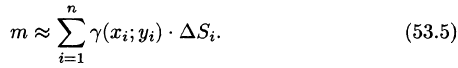
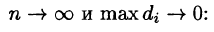
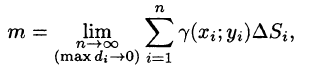
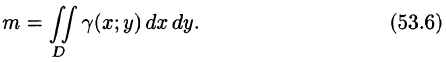
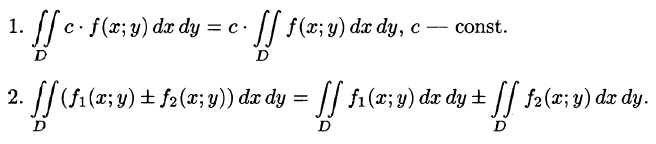
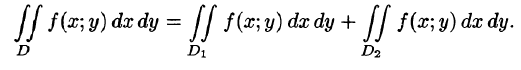
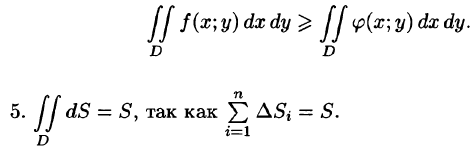
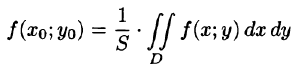
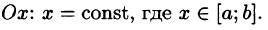
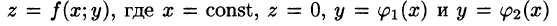
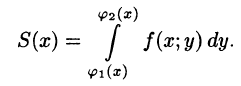
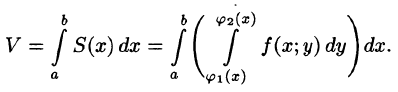
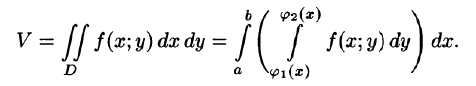
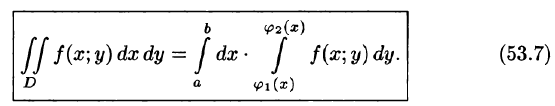
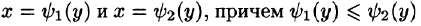
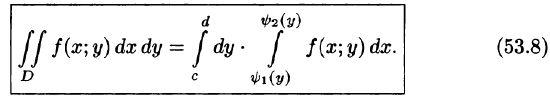
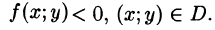
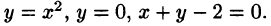
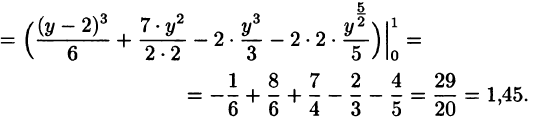
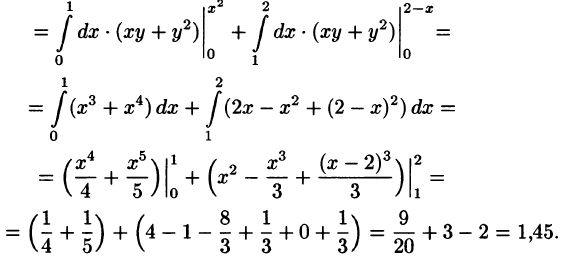
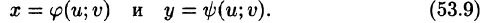

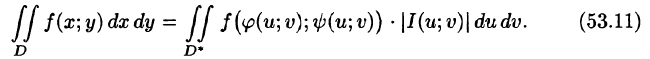
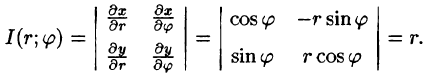
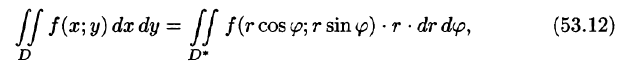
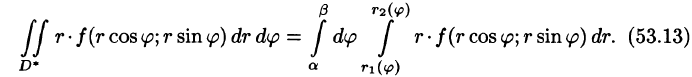
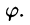
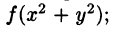 область Dесть круг, кольцо или часть таковых.
область Dесть круг, кольцо или часть таковых.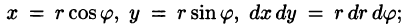 уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по
уравнения линий, ограничивающих область D, также преобразуются к полярным координатам. Преобразование области D в область D* не выполняют, а, совместив декартову и полярную системы координат, находят нужные пределы интегрирования по 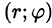 при ее отождествлении с точкой (х; у) области D).
при ее отождествлении с точкой (х; у) области D).