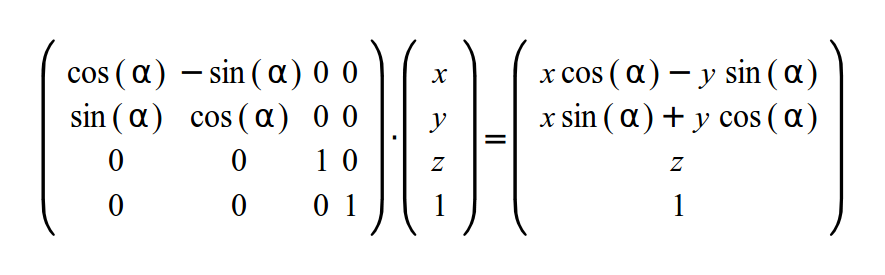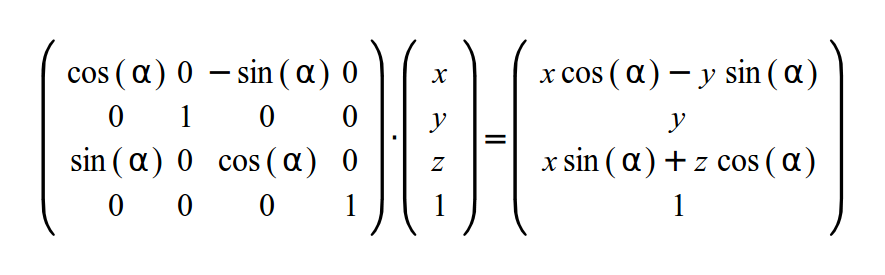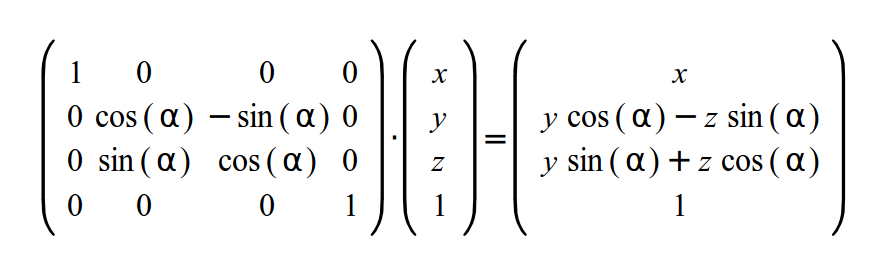- Урок 07 — Вращение
- Прямиком к коду!
- Вращение, движение, масштабирование и проекции в OpenGL под Lazarus
- Комментарии
- OpenGL ES: Перемещение в 3D
- Мифическая камера
- Работа с «gluLookAt()»
- Перемещение в 3D
- Готовимся к перемещению
- Коснись меня
- Теория перемещений в 3D
- Обработка событий с преобразованием в движения
- Сводим воедино
- 💥 Видео
Видео:Физика - движение по окружностиСкачать

Урок 07 — Вращение
Следующий на очереди трансформаций — это вращение, то есть, берется угол и точка, которую мы хотим вращать относительно оси. Для этого всегда будут меняться 2 координаты из 3 (X, Y и Z), а одна останется без изменений. Это значит, что путь будет лежать на одной из 3-х основных плоскостей: XY (когда вращение вокруг Z), YZ (повороты относительно X) и XZ (для Y оси). Можно подобрать преобразования для вращения вокруг произвольной оси, но они довольно сложные и пока что нам не нужны.
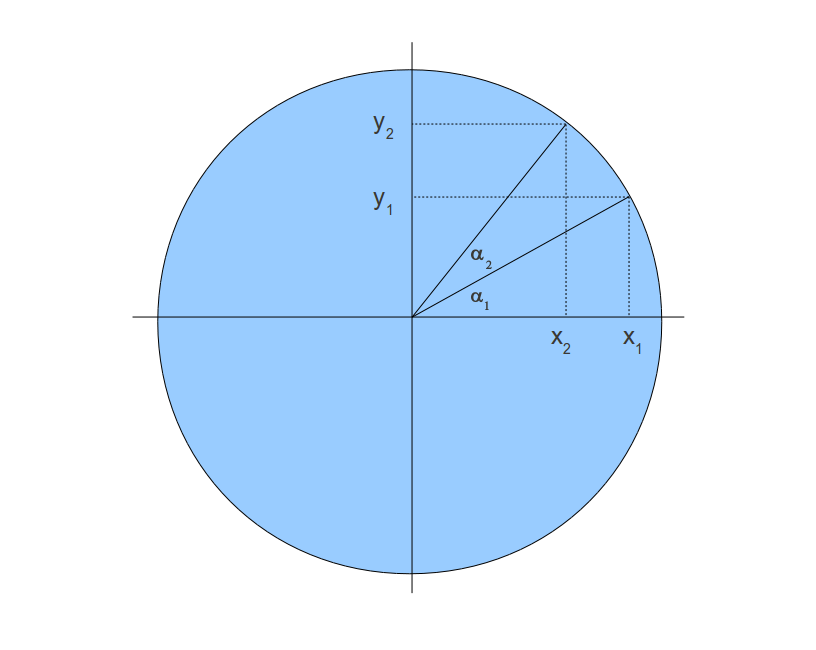
Давайте определим задачу в общих чертах. Сосредоточимся на следующей диаграмме:
Мы хотим двигаться по окружности из (x1,y1) в (x2,y2). Другими словами, мы хотим повернуть точку (x1,y1) на угол a2. Предположим, что радиус окружности равен 1. Это означает следующее: x1=cos(a1) y1=sin(a1) x2=cos(a1+a2) y2=sin(a1+a2)
Мы будем использовать следующие тригонометрические тождества для нахождения x2 и y2: cos(a+b) = cosacosb — sina sinb sin(a+b) = sinacosb+cosa sinb
В диаграмме мы смотрим на плоскость XY, а ось Z — это точка. Если X&Y части 4-вектора, тогда уравнения выше можно записать в форме матрицы (не затрагивая Z&W):
Если мы хотим задать вращение для Y и X осей, то выражения будут похожи, а вот матрицы устроены слегка по другому. Вот матрица для вращения вокруг Y оси:
И матрица вращения вокруг X оси:
Видео:АЛГОРИТМ ДВИЖЕНИЯ ПО ОКРУЖНОСТИСкачать

Прямиком к коду!
Изменения кода в этом уроке очень малы. Мы только изменяем значения единственной матрицы преобразований.
Легко заметить, что мы задали вращение вокруг Z оси. Вы можете попробовать вращение вокруг других осей, но мне кажется, что без настоящей проекции из 3D в 2D другие типы вращения будут выглядеть немного странно. Мы их реализуем в классе полноценного конвейера в следующих уроках.
Видео:Базовый курс C++ (MIPT, ILab). Lecture 14 (доп). OpenGL и VulkanСкачать

Вращение, движение, масштабирование и проекции в OpenGL под Lazarus
В OpenGL используются основные три системы координат: левосторонняя, правосторонняя и оконная. Первые две системы являются трехмерными и отличаются друг от друга направлением оси z: в правосторонней она направлена на наблюдателя, в левосторонней – в глубину экрана. Ось x направлена вправо относительно наблюдателя, ось y – вверх.
Системы координат в OpenGL
Строго говоря, OpenGL позволяет путем манипуляций с матрицами моделировать как правую, так и левую систему координат. Но на данном этапе лучше пойти простым путем и запомнить: основной системой координат OpenGL является правосторонняя система.
РАБОТА С МАТРИЦАМИ
Для задания различных преобразований объектов сцены в OpenGL используются операции над матрицами, при этом различают три типа матриц: модельно-видовая, матрица проекций и матрица текстуры. Все они имеют размер 4×4. Видовая матрица определяет преобразования объекта в мировых координатах, такие как параллельный перенос, изменение масштаба и поворот. Матрица проекций определяет, как будут проецироваться трехмерные объекты на плоскость экрана (в оконные координаты), а матрица текстуры определяет наложение текстуры на объект.
Умножение координат на матрицы происходит в момент вызова соответствующей команды OpenGL, определяющей координату (как правило, это команда glVertex*)
Для того чтобы выбрать, какую матрицу надо изменить, используется команда:
включает режим работы с модельно-видовой матрицей, матрицей проекций, или матрицей текстуры соответственно. Для вызова команд, задающих матрицы того или иного типа, необходимо сначала установить соответствующий режим.
Для определения элементов матрицы текущего типа вызывается команда
где m указывает на массив из 16 элементов типа float или double в соответствии с названием команды, при этом сначала в нем должен быть записан первый столбец матрицы, затем второй, третий и четвертый. Еще раз обратим внимание: в массиве m матрица записана по столбцам.
Часто бывает необходимо сохранить содержимое текущей матрицы для дальнейшего использования, для чего применяются команды
МОДЕЛЬНО-ВИДОВЫЕ ПРЕОБРАЗОВАНИЯ
К модельно-видовым преобразованиям будем относить перенос, поворот и изменение масштаба вдоль координатных осей. Для проведения этих операций достаточно умножить на соответствующую матрицу каждую вершину объекта и получить измененные координаты этой вершины.
Сама матрица может быть создана с помощью следующих команд:
glTranlsate*() производит перенос объекта, прибавляя к координатам его вершин значения своих параметров.
glRotate*() производит поворот объекта против часовой стрелки на угол angle (измеряется в градусах) вокруг вектора (x,y,z).
glScale*() производит масштабирование объекта (сжатие или растяжение) вдоль вектора (x,y,z), умножая соответствующие координаты его вершин на значения своих параметров.
Все эти преобразования изменяют текущую матрицу, а поэтому применяются к примитивам, которые определяются позже. В случае, если надо, например, повернуть один объект сцены, а другой оставить неподвижным, удобно сначала сохранить текущую видовую матрицу в стеке командой glPushMatrix(), затем вызвать glRotate() с нужными параметрами, описать примитивы, из которых состоит этот объект, а затем восстановить текущую матрицу командой glPopMatrix().
Чтобы изображенная фигура выглядела пространственной, систему координат разворачивают вокруг оси X и вокруг оси Y.
ПРОЕКЦИИ
В OpenGL существуют стандартные команды для задания ортографической (параллельной) и перспективной проекций. Первый тип проекции может быть задан командами
Место команд в программе.
Для того чтобы при каждой последующей перерисовке экрана не происходило изменение размеров сцены, связанное с переносом и проецированием, следует использовать видовые команды по определенным правилам.
Первый способ – использование команды glLoadIdentity:
Второй способ – использование команд glPushMatrix и glPopMatrix:
ПРОГРАММА — ПРИМЕР ВРАЩЕНИЯ КУБА В LAZARUS НА OPENGL
Разместите на форме три компонента
Примечание. Обратите внимание для установки компонента TOpenGLControl смотрите урок «Подключение и работа с OpenGL в Lazarus под Windows».
Пропишите на события создания формы Form1: OnFormCreate, нажатия кнопки Form1: OnButton1Click и работы таймера Form1: OnTimer1Timer следующий код:
Видео:OpenGL - Урок 2 - точка, линия, треугольник, кругСкачать
Комментарии
Timer1 — выдает ошибку. Использовал IdleTimer1, работает!
unit Unit1;
uses
Classes, SysUtils, FileUtil, Forms, Controls, Graphics, Dialogs, StdCtrls,
ExtCtrls, OpenGLContext, GL, GLU;
TForm1 = class(TForm)
Button1: TButton;
Button2: TButton;
IdleTimer1: TIdleTimer;
Panel1: TPanel;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure IdleTimer1Timer(Sender: TObject);
private
public
OpenGLControl1: TOpenGLControl; // Контекст воспроизведения OpenGL
cube_rotation: GLFloat;
Speed: Double;
end;
var
Form1: TForm1;
procedure TForm1.Button1Click(Sender: TObject);
begin
glClearColor(1.0, 1.0, 1.0, 1.0);
glClear(GL_COLOR_BUFFER_BIT or GL_DEPTH_BUFFER_BIT);
glEnable(GL_DEPTH_TEST);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(45.0, double(width) / height, 0.1, 100.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(0.0, 0.0,-6.0);
glRotatef(cube_rotation, 1.0, 1.0, 1.0);
glBegin(GL_QUADS);
glColor3f(0.0,1.0,0.0); // Set The Color To Green
glVertex3f( 1.0, 1.0,-1.0); // Top Right Of The Quad (Top)
glVertex3f(-1.0, 1.0,-1.0); // Top Left Of The Quad (Top)
glVertex3f(-1.0, 1.0, 1.0); // Bottom Left Of The Quad (Top)
glVertex3f( 1.0, 1.0, 1.0); // Bottom Right Of The Quad (Top)
glEnd();
glBegin(GL_QUADS);
glColor3f(1.0,0.5,0.0); // Set The Color To Orange
glVertex3f( 1.0,-1.0, 1.0); // Top Right Of The Quad (Bottom)
glVertex3f(-1.0,-1.0, 1.0); // Top Left Of The Quad (Bottom)
glVertex3f(-1.0,-1.0,-1.0); // Bottom Left Of The Quad (Bottom)
glVertex3f( 1.0,-1.0,-1.0); // Bottom Right Of The Quad (Bottom)
glEnd();
glBegin(GL_QUADS);
glColor3f(1.0,0.0,0.0); // Set The Color To Red
glVertex3f( 1.0, 1.0, 1.0); // Top Right Of The Quad (Front)
glVertex3f(-1.0, 1.0, 1.0); // Top Left Of The Quad (Front)
glVertex3f(-1.0,-1.0, 1.0); // Bottom Left Of The Quad (Front)
glVertex3f( 1.0,-1.0, 1.0); // Bottom Right Of The Quad (Front)
glEnd();
glBegin(GL_QUADS);
glColor3f(1.0,1.0,0.0); // Set The Color To Yellow
glVertex3f( 1.0,-1.0,-1.0); // Bottom Left Of The Quad (Back)
glVertex3f(-1.0,-1.0,-1.0); // Bottom Right Of The Quad (Back)
glVertex3f(-1.0, 1.0,-1.0); // Top Right Of The Quad (Back)
glVertex3f( 1.0, 1.0,-1.0); // Top Left Of The Quad (Back)
glEnd();
glBegin(GL_QUADS);
glColor3f(0.0,0.0,1.0); // Set The Color To Blue
glVertex3f(-1.0, 1.0, 1.0); // Top Right Of The Quad (Left)
glVertex3f(-1.0, 1.0,-1.0); // Top Left Of The Quad (Left)
glVertex3f(-1.0,-1.0,-1.0); // Bottom Left Of The Quad (Left)
glVertex3f(-1.0,-1.0, 1.0); // Bottom Right Of The Quad (Left)
glEnd();
glBegin(GL_QUADS);
glColor3f(1.0,0.0,1.0); // Set The Color To Violet
glVertex3f( 1.0, 1.0,-1.0); // Top Right Of The Quad (Right)
glVertex3f( 1.0, 1.0, 1.0); // Top Left Of The Quad (Right)
glVertex3f( 1.0,-1.0, 1.0); // Bottom Left Of The Quad (Right)
glVertex3f( 1.0,-1.0,-1.0); // Bottom Right Of The Quad (Right)
glEnd();
cube_rotation += 5.15 * Speed;
procedure TForm1.Button2Click(Sender: TObject);
begin
if IdleTimer1.Enabled = true then
begin
IdleTimer1.Enabled := false;
Button2.Caption:=’Вращать автоматически’;
end
else
begin
IdleTimer1.Enabled := true;
Button2.Caption:=’Остановить вращение’;
end;
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
// Создание контекста воспроизведения OpenGL и привязка его к панели на форме
OpenGLControl1:=TOpenGLControl.Create(Self);
with OpenGLControl1 do begin
Name:=’OpenGLControl1′;
Align:=alClient;
Parent:=Panel1;
end;
IdleTimer1.Enabled := false;
IdleTimer1.Interval := 100;
Speed := 1;
Button2.Caption:=’Вращать автоматически’;
Button1.Caption:=’Повернуть’;
end;
procedure TForm1.IdleTimer1Timer(Sender: TObject);
begin
Button1Click(Sender);
end;
Видео:Урок 89. Движение по окружности (ч.1)Скачать

OpenGL ES: Перемещение в 3D

Нам предстоит освоить код обработки событий, который позволит ходить «по полу». С помощью касаний мы будем поворачивать влево, вправо, перемещаться вперед и назад. Обойдемся без бега, поворотов головы и наведения резкости, хотя добавить их легко. Подобные ограничения объясняются как желанием упростить изложение, так и возможностью для не располагающих iPod Touch или iPhone добиваться аналогичных результатов в симуляторе.
Кода там не много — в основном объяснения, что и как происходит.
Видео:Speed Coding (OpenGL & C++) - Рисование окружностейСкачать

Мифическая камера
Большинство воспринимает 3D миры как пространство, на которое смотришь через камеру, но в OpenGL камеры как таковой нет. Для иллюзии движения по сцене относительно начальной точки (0, 0, 0) перемещаются объекты, а не камера, как в кино.
Процесс может показаться трудоемким, но это не так. В зависимости от приложения есть множество способов решения данной задачи и еще больше — оптимизации для действительно больших миров. На этом я вкратце остановлюсь чуть позже.
Чтобы немного упростить работу, к уроку я приложил удобную игрушку от «большого брата» OpenGL ES — библиотеки GLU: я имею в виду функцию «gluLookAt()«.
Хотя в этих статьях я редко упоминаю OpenGL, думаю, что с библиотекой GLU знакомы практически все. К сожалению, она не входит в спецификации OpenGL ES, но это не означает, что мы не сможем воспользоваться полезными нам функциями. Для работы с ними не обязательно переносить всю библиотеку — выберите лишь актуальные для вас опции.
Функцию «gluLookAt()» я взял из релиза SGI Open Source. Выбор объясняется исключительно тем, что она оказалась под рукой, а я знаком с принципами ее работы. Лицензия на функцию находится здесь же в коде (автором кода являюсь не я). Для тех, кого этот вариант по тем или иным причинам не устраивает, есть масса альтернатив из открытых источников.
Если решите работать с другим кодом или импортировать иные функции, не забудьте поменять все «GLdouble» на «GLfloat«, а все привязанные к gl вызовы на версии с плавающей запятой. Еще одна общая рекомендация — избегайте всего, что ориентировано на пользовательский интерфейс (функции ввода, окна). В целом, моментов, на которые нужно обращать внимание, масса, но остальные достаточно очевидны.
Для профессиональных целей ищите последние обновления бесплатных версий. Замечу, что Mesa не рекомендуют сами создатели — она не обновляется, активная разработка приостановлена. Я знаю, что в Интернет есть код для iPhone на базе Mesa GLU, но для профессионального применения он не подходит (читай: содержит ошибки).
Если кому-то интересно, почему разработчики вместо своей библиотеки рекомендуют SGI или другие решения, поищите информацию на сайте Mesa.
Видео:OpenGL - Урок 9 - Ортогональная и перспективная проекции. Буфер глубины (Z-буфер)Скачать

Работа с «gluLookAt()»
Освоив функцию «gluLookAt()«, вы обязательно оцените ее простоту и удобство. Посмотрим на прототип:
void gluLookAt( GLfloat eyex,
GLfloat eyey,
GLfloat eyez,
GLfloat centerx,
GLfloat centery,
GLfloat centerz,
GLfloat upx,
GLfloat upy,
GLfloat upz)
Согласен, 9 параметров временами многовато, но здесь главное — разобраться. Первые три характеризуют позицию зрителя (это просто координаты X, Y, Z).
Вторые три относятся к рассматриваемому объекту (вновь трио X, Y, Z).
Последние три можно объединить в вектор «вверх». Сейчас мы их рассматривать не будем, поскольку нужный эффект дают именно две первые позиции.
Координаты зрителя (глаз) — это и есть мифическая камера. Естественно, они соотносятся с координатами пространства. Фактически, это точка в пространстве, откуда вы наблюдаете за происходящим. Координаты «center» соответствуют направлению взгляда, т.е. его цели. Если координата «center» Y находится выше координаты взгляда Y, пользователь смотрит вверх. Если меньше, то, соответственно, — вниз.
Наш базовый проект уже настроен, но без перемещений. Мы нарисовали пол и смотрим в никуда:
Вот что получится при щелчке на кнопке «Build and Go«.
Для начала попробуем поработать с функцией «glLookAt()«. Перейдите к методу «drawView:» и после вызова «glLoadIdentity()» добавьте приведенный ниже код:
glLoadIdentity();
gluLookAt(5.0, 1.5, 2.0, // Положение глаз, взгляд «из»
-5.0, 1.5, -10.0, // Цель, взгляд «на»
0.0, 1.0, 0.0); // Пока игнорируем
Еще раз щелкните на кнопке «Build and Go«, с удовольствием убедившись, что все работает. Результат в симуляторе должен быть следующим:
Единственным обращением к функции мы перевели взгляд из одного угла в противоположный. Поэкспериментируйте с параметрами «glLookAt()«, наблюдая за происходящим.
Видео:OpenGL - Урок 10 - Первые шаги в 3D. Учимся осматриваться - управление камерой.Скачать

Перемещение в 3D
Теперь, получив представление о «gluLookAt()«, предлагаю воспроизвести прогулку по полу. В действительности двигаться мы будем вдоль двух осей (X и Z, т.е. без изменения высоты), меняя направление с помощью поворота.
Если вспомнить функцию «gluLookAt()«, какая информация, по вашему мнению, нужна для прогулок в трехмерном пространстве?
Понадобятся:
локация зрителя «eye»;
направление взгляда (цель) «centre».
Зная две эти вводные, мы готовы обрабатывать информацию от пользователя, позволяя ему контролировать местонахождение в пространстве.
Предположим, мы решили начать с двух задействованных ранее величин. Пока двигаться не позволяет жестко закодированная информация фрагмента, поэтому для начала перейдем к интерфейсу и добавим следующие переменные:
GLfloat eye[3];// Откуда мы смотрим
GLfloat center[3];// Куда мы смотрим
Названия «eye» и «center» при желании вполне можно заменить на «position» и «facing» — существенного значения это не имеет (я просто использовал термины функции «gluLookAt()«).
Две переменные содержат координаты X, Y и Z. Величину Y можно жестко прописать в коде, т.к. она не меняется, но я решил обойтись без лишних движений.
Переходим к методу «initWithCoder:«. Здесь инициализируем две переменные со значениями, использованными ранее для обращения к «gluLookAt()«:
eye[0] = 5.0;
eye[1] = 1.5;
eye[2] = 2.0;
center[0] = -5.0;
center[1] = 1.5;
center[2] = -10.0;
Возвращаемся к методу «drawView:«. Вызов «gluLookAt()» измените на:
gluLookAt(eye[0], eye[1], eye[2], center[0], center[1], center[2],
0.0, 1.0, 0.0);
Для полного спокойствия щелкните на кнопке «Build & Go«, убедившись, что все работает.
Видео:Движение тела по окружности с постоянной по модулю скоростью | Физика 9 класс #18 | ИнфоурокСкачать

Готовимся к перемещению
Прежде чем мы сможем обрабатывать события, перемещаясь в пространстве, необходимо настроить ряд моментов в заголовочном файле. Переключитесь на него, чтобы задать несколько настроек по умолчанию и создать новый тип перечня.
Для начала определимся со скоростью ходьбы и поворотов:
#define WALK_SPEED 0.005
#define TURN_SPEED 0.01
Мне эти значения представляются несколько замедленными, поэтому, разобравшись с их работой, можете внести свои собственные.
Следующим шагом создаем перечислимый тип, чтобы в точности сохранять наши действия. Добавим следующее:
typedef enum __MOVMENT_TYPE <
MTNone = 0,
MTWalkForward,
MTWAlkBackward,
MTTurnLeft,
MTTurnRight
> MovementType;
Теперь в процессе функционирования приложения мы можем стоять (MTNone), идти вперед, назад, поворачиваться влево и вправо. Боюсь, что этим пока нам придется и ограничиться.
Осталось указать переменную, содержащую текущее движение:
Не забудьте перейти к методу «initWithCoder:» и задать значение по умолчанию для переменной «currentMovement«:
По умолчанию это значение для переменной будет таковым в любом случае, но подобные действия — хорошая практика.
Видео:Three.js - Движение по окружностиСкачать

Коснись меня
Разобравшись с основами, можно переходить собственно к обработке касаний. Если помните, в прошлом уроке я представил все четыре метода их обработки. На этот раз — для простоты — мы воспользуемся только двумя: «touchesBegan» и «touchesEnded«.
Чтобы определить предпринимаемое действие, экран iPhone я разделил на четыре зоны:
Стандартная высота экрана — 480 пикселей. Делим его на 3 равные части по 160 пикселей. Пиксели 0
160 соответствуют движению вперед, 320
480 — перемещению назад, центральные 160 поделены на правую и левую половины для поворотов.
Вот теперь можно представить первый из методов касания:
— (void)touchesBegan:(NSSet *)touches withEvent:(UIEvent *)event <
UITouch *t = [[touches allObjects] objectAtIndex:0];
CGPoint touchPos = [t locationInView:t.view];
// Определяем позицию на экране. Нас интересуют исключительно
// координаты экрана iPhone, а не пространства
// поскольку мы всего лишь обрабатываем события.
//
// (0, 0)
// +————+
// | |
// | 160 |
// |————| 160
// | | |
// | | |
// |————| 320
// | |
// | |
// +————+ (320, 480)
//
if (touchPos.y 320) <
// Идем назад
currentMovement = MTWAlkBackward;
> else if (touchPos.x
При касании пользователем экрана останется зафиксировать сегмент и указать переменную, чтобы знать, что делать, когда настанет момент расчета нового положения. Не забывайте, что выносить определение метода в интерфейс необходимости нет — такие методы наследуются.
Настала очередь метода «touchesEnded«.
— (void)touchesEnded:(NSSet *)touches withEvent:(UIEvent *)event <
Собственно говоря, все понятно. Теперь нам нужен метод для обработки данных событий касания. На этот раз потребуется декларация метода в интерфейсе. Переключаемся на заголовочный файл и добавляем следующее определение метода:
Переходим обратно и приступаем к его реализации. В этом методе мы будем рассчитывать перемещение по трехмерному пространству.
Видео:OpenGL - Урок 16 - Основы освещения.Скачать

Теория перемещений в 3D
Начнем с базовых понятий. Уверен, никто не удивиться, когда узнает, что это лишь один из способов расчета новых локаций в трехмерном пространстве при n-ном числе перемещений вдоль любого вектора v. К сожалению, не помню, кто первым это сказал (возможно, Arvo). В любом случае, это было давно — еще до того, как Wolf 3D показал, как это происходит в реальном времени.
Первой рассмотрим ходьбу. Если пользователь сообщает о желании идти вперед, нужно не только учитывать вид из локации зрителя, но и не упускать целевой точки. Взгляд из локации сообщает нам о текущем местонахождении, а взгляд на цель определяет направление движения.
Любая картинка лучше тысячи слов: взгляните на изображение, представляющее взгляд из точки и взгляд на цель.
При подобном методе перемещения расстояние между двумя точками является величиной дельта для координат X и дельта для координат Y. Осталось получить новые значения X и Z умножением текущих координат на величину «скорости». Примерно так:
Мы легко рассчитаем новые координаты для красной точки.
Начинаем с deltaX and deltaZ:
deltaX = 1.5 — 1.0 = 0.5
deltaZ = -10 — (- 5.0) = -5.0
Умножаем на скорость ходьбы:
xDisplacement = deltaX * WALK_SPEED
= 0.5 * 0.01
= 0.005
zDisplacement = deltaZ * WALK_SPEED
= -5.0 * 0.01
= 0.05
Соответственно, новая координата, представленная на рисунке выше красной точкой:eyeC + CDisplacement
(eyex + xDisplacement, eyey, eyez + zDisplacement)
= (0.005+1.0, eyey,(-10)+ 0.05)
= (1.005, eyey, -9.95)
Замечу, что предложенный метод не лишен недостатков. Основная проблема в том, что чем больше расстояние между локацией зрителя и объектом взгляда, чем выше «скорость ходьбы». Тем не менее, вопрос решаем, а с точки зрения ресурсов CPU менее затратен по сравнению со многими прочими алгоритмами движения.
Размеры нашего мирка невелики, а вот на деле разница между зрителем и объектом взгляда окажется слишком огромной, поэтому обязательно поэкспериментируйте. Как выяснится, скорость перемещения непосредственно зависит от соотношения расстояния между двумя точками и величины «WALK_SPEED«.
Осталось рассмотреть повороты влево/вправо.
Зачастую мне приходится сталкиваться с кодом, в котором программисты ответственно выписывают угол, под которым визуализируется сцена. Это не наш случай. Рабочий угол нам известен, поскольку известны две точки (вспомните Пифагора — у нас правильный треугольник).
Взгляните на рисунок:
Чтобы инициировать поворот, нам нужно всего лишь переместить по кругу взгляд на целевой объект. Наше определение «TURN_SPEED«, фактически, является углом поворота.
Ключ к происходящему: нет необходимости корректировать координаты зрителя — меняется объект взгляда. Откладывая на виртуальной окружности перед глазами новую точку-локацию (т.е. постепенно увеличивая значение угла, определяемое «TURN_SPEED«), получаем новый «угол поворота».
Раз поворот соответствует нарисованному кругу, центральной точкой которого является локация зрителя или точка взгляда, достаточно вспомнить принципы рисования круга.
Другими словами, все сводится к:
newX = eyeX + radius * cos(TURN_SPEED)*deltaX — sin(TURN_SPEED)*deltaZ
newZ = eyeZ + radius * sin(TURN_SPEED)* deltaX +
cos(TURN_SPEED)*deltaZ
Видео:OpenGL - Урок 30 - Как отобразить текст. Самый простой способ.Скачать

Обработка событий с преобразованием в движения
Опробуем изложенное на практике.
Вернувшись к реализации, оттолкнемся от касаний, чтобы получить новые параметры для «gluLookAt()«. Начнем с метода реализации и парочки базовых принципов:
if (currentMovement == MTNone) <
// Мы идем в никуда, и делать там нечего
return;
>
Для начала проверяем факт перемещения. Если он отсутствует, делать больше нечего.
Независимо от того, движемся мы или поворачиваемся, необходимо знать значения «deltaX» и «deltaZ«. Сохраняю их в вызываемом переменной векторе:
vector[0] = center[0] — eye[0];
vector[1] = center[1] — eye[1];
vector[2] = center[2] — eye[2];
Я рассчитал и значение Y delta, хотя нам оно не нужно.
Теперь выясняем, какие действия по перемещению предпринимать. Все содержится в операторе выбора:
switch (currentMovement) <
case MTWalkForward:
eye[0] += vector[0] * WALK_SPEED;
eye[2] += vector[2] * WALK_SPEED;
center[0] += vector[0] * WALK_SPEED;
center[2] += vector[2] * WALK_SPEED;
break;
case MTWAlkBackward:
eye[0] -= vector[0] * WALK_SPEED;
eye[2] -= vector[2] * WALK_SPEED;
center[0] -= vector[0] * WALK_SPEED;
center[2] -= vector[2] * WALK_SPEED;
break;
case MTTurnLeft:
center[0] = eye[0] + cos(-TURN_SPEED)*vector[0] —
sin(-TURN_SPEED)*vector[2];
center[2] = eye[2] + sin(-TURN_SPEED)*vector[0] +
cos(-TURN_SPEED)*vector[2];
break;
case MTTurnRight:
center[0] = eye[0] + cos(TURN_SPEED)*vector[0] — sin(TURN_SPEED)*vector[2];
center[2] = eye[2] + sin(TURN_SPEED)*vector[0] + cos(TURN_SPEED)*vector[2];
break;
>
>
Вот и весь метод обработки касаний. Реализация представляет собой уже рассмотренный нами ранее алгоритм.
Видео:OpenGL - Урок 3 - Матрица преобразований. Перемещение, вращение, масштаб.Скачать

Сводим воедино
Вернитесь к методу «drawView» и перед вызовом «gluLookAt():» добавьте следующую строку:
[self handleTouches];
[self handleTouches];
Все готово!
Можно щелкать на кнопке «Build and Go» — прямо сейчас!
Исходный код к уроку можно скачать здесь.
💥 Видео
OpenGL - Урок 36 - VBO (Vertex Buffer Object). Буфер вершин.Скачать

Кинематика. Движение по окружности. Лекция 1-2Скачать

ВРАЩЕНИЕ В КООРДИНАТАХ. КВАТЕРНИОНЫ И УГЛЫ ЭЙЛЕРА - С++ OpenGL ЧАСТЬ #3Скачать

OpenGL - Урок 12 - Как создать простое меню. Обработка изменения размера окна.Скачать