Две прямые не пересекаются чтобы утверждать что эти прямые параллельны

Две прямые называются параллельными, если, находясь в одной плоскости, они не пересекаются, сколько бы их ни продолжали. Параллельность прямых на письме обозначают так: AB || СE

Возможность существования таких прямых доказывается теоремой.

Теорема.

Через всякую точку, взятую вне данной прямой, можно провести параллельную этой прямой.

Пусть AB данная прямая и С какая-нибудь точка, взятая вне ее. Требуется доказать, что через С можно провести прямую, параллельную AB. Опустим на AB из точки С перпендикуляр СD и затем проведем СE ^ СD, что возможно. Прямая CE параллельна AB.

Для доказательства допустим противное, т.е., что CE пересекается с AB в некоторой точке M. Тогда из точки M к прямой СD мы имели бы два различных перпендикуляра MD и MС, что невозможно. Значит, CE не может пересечься с AB, т.е. СE параллельна AB.

Следствие.

Аксиома параллельных линий.

Через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой.

Так, если прямая СD, проведенная через точку С параллельна прямой AB, то всякая другая прямая СE, проведенная через ту же точку С, не может быть параллельна AB, т.е. она при продолжении пересечется с AB.

Доказательство этой не вполне очевидной истины оказывается невозможным. Ее принимают без доказательства, как необходимое допущение (postulatum).

Следствия.

1. Если прямая (СE) пересекается с одной из параллельных (СВ), то она пересекается и с другой (AB), потому что в противном случае через одну и ту же точку С проходили бы две различные прямые, параллельные AB, что невозможно.

2. Если каждая из двух прямых (A и B) параллельны одной и той же третьей прямой (С), то они параллельны между собой.

Действительно, если предположить, что A и B пересекаются в некоторой точке M, то тогда через эту точку проходили бы две различные прямые, параллельные С, что невозможно.

Теорема.

Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой параллельной.

Перпендикуляр EF, пересекаясь с AB, непременно пересечет и СD. Пусть точка пересечения будет H.

Предположим теперь, что СD не перпендикулярна к EH. Тогда какая-нибудь другая прямая, например HK, будет перпендикулярна к EH и, следовательно через одну и ту же точку H будут проходить две прямые параллельные AB: одна СD, по условию, а другая HK по доказанному раньше. Так как это невозможно, то нельзя допустить, что СВ была не перпендикулярна к EH.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Две прямые параллельны одни и той же плоскости?

Геометрия | 10 — 11 классы

Две прямые параллельны одни и той же плоскости.

Можно ли утвердить что эти прямые пароллельны между собой?

Если нет то каково их взаимное положение.

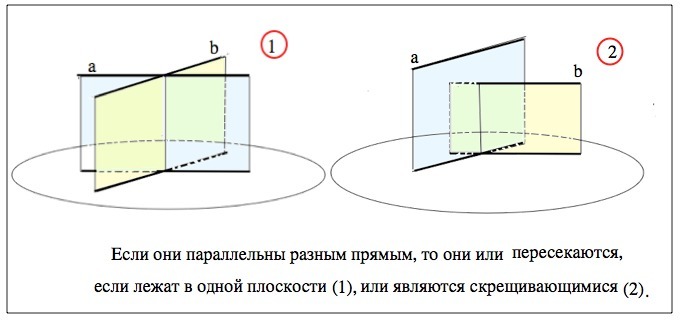
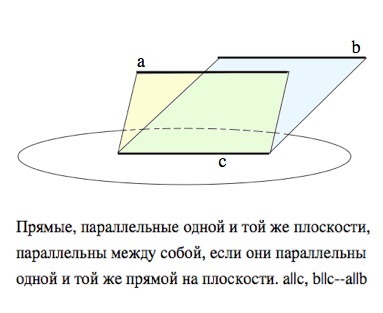
Прямые, параллельные одной и той же плоскости, параллельны между собой, если они параллельны одной и той же прямой на плоскости.

Если они параллельны разным прямым, то они или пересекаются, если лежат в одной плоскости, или являются скрещивающимися.

(см. рисунки вложения).

Видео:№7. Две прямые пересекаются в точке М. Докажите, что все прямые, не проходящие через точкуСкачать

Верно ли утверждение?

Верно ли утверждение?

Плоскости параллельны, если две прямые лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости.

Видео:Теорема 13.2 Если две прямые параллельны третьей, то они параллельны ||Геометрия 7 класс||Скачать

Вариант II 1?

Что можно сказать о взаимном положении двух плоскостей, имею­щих три общие точки, не лежащие на одной прямой?

2. Могут ли две различные плоскости иметь только две общие точки?

Прямые а и b пересекаются в точке М.

Прямая с, не проходящая че­рез точку М, пересекает прямые а и b.

Лежат ли все эти три прямые в од­ной плоскости?

Каково взаимное положение прямых : 1) A 1D и MN ; 2) A 1D и В 1С ; 3) MN и А 1В1(Рис.

1). Прямые а и b скрещиваются с прямой с.

Могут ли прямые а и b быть параллельными?

Две прямые параллельны одной и той же плоскости.

Можно ли ут­верждать, что эти прямые параллельны между собой?

Если нет, то каково их взаимное положение?

На рисунке 2 прямые тип параллельны.

Точки А и В соответст­венно принадлежат прямым тип ; b лежит в плоскости α, а b.

Каково взаимное положение прямых b и с?

Даны четырехугольник ABCD и плоскость α.

Его диагонали АС и BD параллельны плоскости α.

Каково взаимное положение АВ и плоско­сти α?

Плоскости α и β параллельны.

Пересекающиеся в точ­ке М прямые а и b пересекают плоскость α соответственно в точках В и А, а плоскость β — в точках Е и F Найдите отношение 10.

Плоскость α проходит через диагональ основания параллелепипе­да и середину одной из сторон верхнего основания.

Определите вид сече­ния.

Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Две плоскости параллельны одной прямой?

Две плоскости параллельны одной прямой.

Параллельны ли они между собой?

Видео:Теорема 13.1. Две прямые, перпендикулярные третьей прямой, параллельны || Геометрия 7 класс ||Скачать

Даны треугольник АВС и плоскость а, АВ || а, АС || а?

Даны треугольник АВС и плоскость а, АВ || а, АС || а.

Каково взаимное положение прямой ВС и плоскости А?

Видео:7 класс, 25 урок, Признаки параллельности двух прямыхСкачать

Плоскости и пересекаются по прямой c?

Плоскости и пересекаются по прямой c.

В плоскости a проведена прямая a которая параллельна прямой c.

Каково взаимное расположение прямой a и плоскости b?

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Пожалуйстаааа, помогите?

Выберите номера верных утверждений :

Если две прямые в пространстве параллельны третьей прямой, то эти прямые параллельны или совпадают.

2. Если две плоскости в пространстве параллельны третьей плоскости, то эти плоскости параллельны или совпадают.

3. Если две прямые в пространстве параллельны одной плоскости, то эти прямые параллельны или совпадают.

Видео:Параллельность прямых. 10 класс.Скачать

Две плоскости пересекаются по прямой с?

Две плоскости пересекаются по прямой с.

Можно ли в каждой из плоскостей провести по прямой так, чтобы они были параллельны между собой и не были параллельны линии пересечения с?

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Если две пересекающие прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то как расположены эти плоскости?

Если две пересекающие прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то как расположены эти плоскости?

Видео:Параллельные прямые. 6 класс.Скачать

Две прямые параллельны одной плоскости ?

Две прямые параллельны одной плоскости .

Можно ли утверждать , что эти прямые параллельны?

Видео:Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?

Верно ли утверждение, что плоскости параллельны, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?

Перед вами страница с вопросом Две прямые параллельны одни и той же плоскости?, который относится к категории Геометрия. Уровень сложности соответствует учебной программе для учащихся 10 — 11 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

В правильной шестиугольной пирамиде SABCDEF AF = 2, SD = √17. Найдите площадь боковой поверхности пирамиды.

TgB = AC / BC = 3 / 5 = 0, 6 Ответ : 0, 6.

Угол АСВ в 2 раза 173 : 2 = 86, 5°.

Решение смотри в файле.

Оби элементарные 1. По т. Пифагора x ^ 2 = 225 — 81 x = 12 Ответ : 12 ; 2. S = (BC + AD) / 2 * BH.

Ответ : 11 см, 11 см, 17 см, 17 см. Объяснение : противоположные стороны параллелограмма равны. Полупериметр параллелограмма (сумма двух смежных сторон) а + в = р = 56 : 2 = 28 см. А = в + 6Составим уравнение : в + в + 6 = 282в = 22в = 11 см, тогд..

∠XOZ = ∠ZOV + ∠VOY + ∠YOU + ∠UOX По условию задачи ∠ ZOV = ∠VOY, ∠YOU = ∠UOX, поэтому ∠XOZ = 2∠VOY + 2∠YOU = 2 * ∠UOV = 2 * 80 = 160°Ответ : ∠XOZ = 160°.

Во втором не знаю как доказать, извиняюсь.

Рассмотрим треугольник АDB и треугольник ACB : угол CA = углу ABD , угол АBD = углу DBA Сторона AB — общая . Значит треугольник ACB = треугольнику BDA по второму признаку равенства треугольников . Тогда AC = BD = 13см.

Так как∆АВС и∆АДС равнобедренные, то АД = ДС АВ = ВС Что бы получить АБД и СВД нужно провести от точки Д до точки Б прямую, она же будет общей стороной. Значит по третьему признаку равенства треугольников∆АВД = ∆СВД.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Параллельные прямые, признаки и условия параллельности прямых

В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.

Видео:Стереометрия для ЕГЭ: 2 - параллельные и скрещивающиеся прямыеСкачать

Параллельные прямые: основные сведения

Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

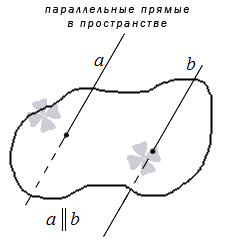
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.

Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.

Чтобы обозначить параллельность прямых, общепринято использовать символ ∥ . Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b . Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b , или прямая b параллельна прямой а .

Сформулируем утверждение, играющее важную роль в изучаемой теме.

Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.

В случае, когда речь идет о пространстве, верна теорема:

Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.

Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10 — 11 классов).

Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Параллельность прямых: признаки и условия параллельности

Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.

В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.

Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.

Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.

Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.

Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.

Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

Доказательство указанных условий присутствует в программе геометрии за 7 — 9 классы.

В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.

Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.

На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.

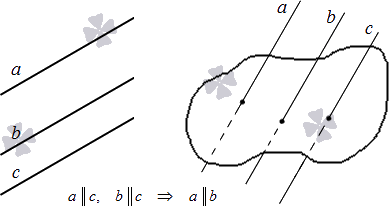
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.

Доказательство признака изучается в программе геометрии 10 класса.

Дадим иллюстрацию указанных теорем:

Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.

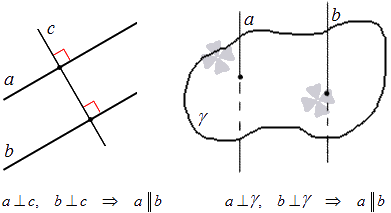
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Сформулируем аналогичное для трехмерного пространства.

В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.

Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.

Видео:Параллельные прямые (задачи).Скачать

Параллельность прямых в прямоугольной системе координат

В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.

Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.

Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.

Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.

Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a → = ( a x , a y ) и b → = ( b x , b y ) являются направляющими векторами прямых a и b ;

и n b → = ( n b x , n b y ) являются нормальными векторами прямых a и b , то указанное выше необходимое и достаточное условие запишем так: a → = t · b → ⇔ a x = t · b x a y = t · b y или n a → = t · n b → ⇔ n a x = t · n b x n a y = t · n b y или a → , n b → = 0 ⇔ a x · n b x + a y · n b y = 0 , где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.

1. Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A 1 x + B 1 y + C 1 = 0 ; прямая b — A 2 x + B 2 y + C 2 = 0 . Тогда нормальные векторы заданных прямых будут иметь координаты ( А 1 , В 1 ) и ( А 2 , В 2 ) соответственно. Условие параллельности запишем так:

A 1 = t · A 2 B 1 = t · B 2

1. Прямая a описывается уравнением прямой с угловым коэффициентом вида y = k 1 x + b 1 . Прямая b — y = k 2 x + b 2 . Тогда нормальные векторы заданных прямых будут иметь координаты ( k 1 , — 1 ) и ( k 2 , — 1 ) соответственно, а условие параллельности запишем так:

k 1 = t · k 2 — 1 = t · ( — 1 ) ⇔ k 1 = t · k 2 t = 1 ⇔ k 1 = k 2

Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.

1. Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x — x 1 a x = y — y 1 a y и x — x 2 b x = y — y 2 b y или параметрическими уравнениями прямой на плоскости: x = x 1 + λ · a x y = y 1 + λ · a y и x = x 2 + λ · b x y = y 2 + λ · b y .

Тогда направляющие векторы заданных прямых будут: a x , a y и b x , b y соответственно, а условие параллельности запишем так:

a x = t · b x a y = t · b y

Заданы две прямые: 2 x — 3 y + 1 = 0 и x 1 2 + y 5 = 1 . Необходимо определить, параллельны ли они.

Решение

Запишем уравнение прямой в отрезках в виде общего уравнения:

x 1 2 + y 5 = 1 ⇔ 2 x + 1 5 y — 1 = 0

Мы видим, что n a → = ( 2 , — 3 ) — нормальный вектор прямой 2 x — 3 y + 1 = 0 , а n b → = 2 , 1 5 — нормальный вектор прямой x 1 2 + y 5 = 1 .

Полученные векторы не являются коллинеарными, т.к. не существует такого значения t , при котором будет верно равенство:

2 = t · 2 — 3 = t · 1 5 ⇔ t = 1 — 3 = t · 1 5 ⇔ t = 1 — 3 = 1 5

Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.

Ответ: заданные прямые не параллельны.

Заданы прямые y = 2 x + 1 и x 1 = y — 4 2 . Параллельны ли они?

Решение

Преобразуем каноническое уравнение прямой x 1 = y — 4 2 к уравнению прямой с угловым коэффициентом:

x 1 = y — 4 2 ⇔ 1 · ( y — 4 ) = 2 x ⇔ y = 2 x + 4

Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.

Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2 x + 1 , например, ( 0 , 1 ) , координаты этой точки не отвечают уравнению прямой x 1 = y — 4 2 , а значит прямые не совпадают.

Следующим шагом определим выполнение условия параллельности заданных прямых.

Нормальный вектор прямой y = 2 x + 1 это вектор n a → = ( 2 , — 1 ) , а направляющий вектором второй заданной прямой является b → = ( 1 , 2 ) . Скалярное произведение этих векторов равно нулю:

n a → , b → = 2 · 1 + ( — 1 ) · 2 = 0

Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.

Ответ: данные прямые параллельны.

Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.

Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.

Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t , чтобы выполнялось равенство:

a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z

Заданы прямые x 1 = y — 2 0 = z + 1 — 3 и x = 2 + 2 λ y = 1 z = — 3 — 6 λ . Необходимо доказать параллельность этих прямых.

Решение

Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a → и b → заданных прямых имеют координаты: ( 1 , 0 , — 3 ) и ( 2 , 0 , — 6 ) .

1 = t · 2 0 = t · 0 — 3 = t · — 6 ⇔ t = 1 2 , то a → = 1 2 · b → .

Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.

Ответ: параллельность заданных прямых доказана.

💡 Видео

ГЕОМЕТРИЯ 10 класс : Параллельность прямых, прямой и плоскостиСкачать

Ответы на вопросы к главе 1 - Геометрия 10-11 класс АтанасянСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

№51. Докажите, что плоскости α и β параллельны, если две пересекающиеся прямые mСкачать