Видео:Поступайте правильно Математика ЕГЭСкачать
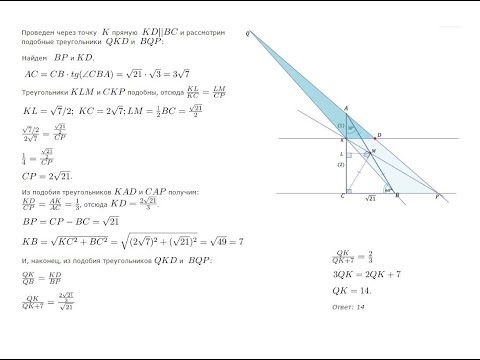
Ваш ответ
Видео:ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать

решение вопроса
Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Похожие вопросы
- Все категории
- экономические 43,283
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,073
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:ЕГЭ Задание 16 Три окружностиСкачать
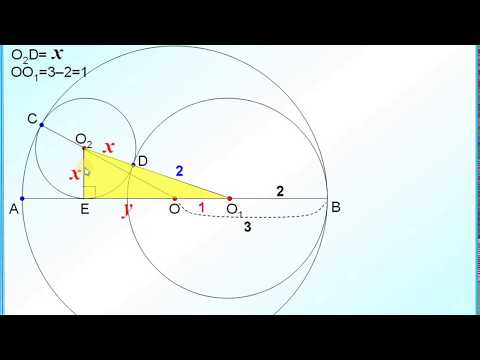
Две окружности внутренне касаются в точке к хорда ав большей
Две окружности касаются внутренним образом в точке K. Пусть AB — хорда большей окружности, касающаяся меньшей окружности в точке L.
а) Докажите, что KL — биссектриса угла AKB.
б) Найдите длину отрезка KL, если известно, что радиусы большей и меньшей окружностей равны соответственно 6 и 2, а угол АKB равен 90°.
а) Продлим AB до пересечение с общей касательной двух окружностей в точке Тогда
(в большой окружности один из них вписанный, а другой — угол между касательной и хордой, поэтому они оба равны половине дуги BK) и
(поскольку
как отрезки касательных к маленькой окружности). Тогда
что и требовалось доказать.
б) По условию AB — диаметр большой окружности. Обозначим центр ее за O, а центр маленькой за Тогда
и, следовательно,
и
Ответ:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать  Задание 16. Математика ЕГЭ. Две окружности касаются внутренним образом в точке К, причем меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке С.Задание. Две окружности касаются внутренним образом в точке К, причем меньшая проходит через центр большей. Хорда MN большей окружности касается меньшей в точке С. Хорды KM и KN пересекают меньшую окружность в точках А и В соответственно, а отрезки КС и АВ пересекаются в точке L. а) Докажите, что CN : CM = LB : LA. б) Найдите MN, если LB : LA = 2 : 3, а радиус малой окружности равен √23. Решение: Точка О – центр большей окружности. Так как окружности касаются внутренним образом и меньшая окружность проходит через центр большей окружности, то КО – диаметр меньшей окружности. Точка В лежит на окружности с диаметром КО, значит, угол ∠КВО = 90°, т. е. отрезок ВО перпендикулярен отрезку KN. Отрезок ВО – высота равнобедренного треугольника ∆KNO, следовательно, ВО – медиана треугольника ∆KNO. Поэтому точка В – середина отрезка KN. Точка А лежит на окружности с диаметром КО, значит, угол ∠КАО = 90°, т. е. отрезок АО перпендикулярен отрезку KМ. Отрезок АО – высота равнобедренного треугольника ∆KМO, следовательно, АО – медиана треугольника ∆KМO. Поэтому точка А – середина отрезка KМ. Тогда АВ – средняя линия треугольника ∆KMN, следовательно, АВ параллельна MN. Треугольники ∆AKL и ∆MKC – подобные треугольники (∠AKL – общий угол, ∠KAL = ∠KMC), следовательно,
Треугольники ∆LKB и ∆CKN – подобные треугольники (∠LKB – общий угол, ∠KLB = ∠KCN), следовательно, Из (1) и (2) равенств получаем: б) Найдите MN, если LB : LA = 2 : 3, а радиус малой окружности равен √23. Пусть 1 часть равна x, тогда CN = 2x, MC = 3x, MN = 5x. В равнобедренном треугольнике ∆MON проведем высоту ОН, высота ОН также является медианой, значит, MH = HN = 2,5x. Из прямоугольного треугольника ∆MOH по теореме Пифагора найдем ОН: ОН 2 = МО 2 – МН 2 ОН 2 = (2√23) 2 – (2,5x) 2 = 92 – 6,25x 2 Проведем OD перпендикулярно QC, DC = OH: OD = CH = MH – MC = 2,5x – 2x = 0,5x. Из прямоугольного треугольника ∆QDO по теореме Пифагора: QO 2 = DO 2 + QD 2 Условию задачи удовлетворяет значение x = 23/6, тогда MN = 5x = 5·(23/6) = 115/6. Почему когда находим OD MC становится 2х,хотя изначально это было 3х?(часть б) 📽️ Видео№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать  ЕГЭ Задание 16 Внутреннее касание двух окружностейСкачать 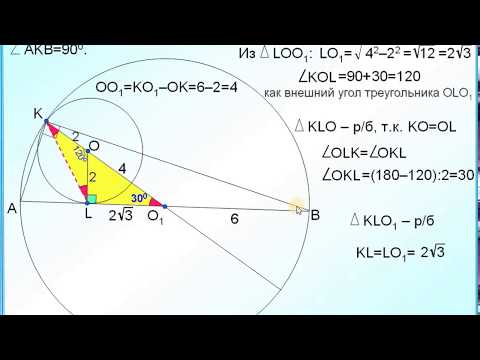 №662 (исправлено) Хорды АВ и CD окружности пересекаются в точке Е. Найдите угол ВЕС, если ∪AD=54°Скачать  ДВИ по математике МГУ Геометрия Решение математикаСкачать  Окружность №16 из ОГЭ. Свойства хорд, касательных, секущих.Скачать  Задача №16. Пересекающиеся и касающиеся окружности.Скачать  №666. Хорды АВ и CD пересекаются в точке Е. Найдите ED, если: а) АЕ = 5, ВЕСкачать  №1 из ЕГЭ 2023 по математике. Лайфхаки для №16. Окружность, вписанные углы, хорды, касательныеСкачать  Задача на нахождение длины хорды окружностиСкачать  ✓ Всё, что нужно знать про окружность | ЕГЭ. Задания 1 и 16. Профильный уровень | Борис ТрушинСкачать  Мини-курс - 16 задание по математике ЕГЭ 2022! Стрим с Анной Малковой - ПланиметрияСкачать  Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать  11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать  Профильный ЕГЭ 2024. Задача 16. Касающиеся окружностиСкачать  Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CDСкачать 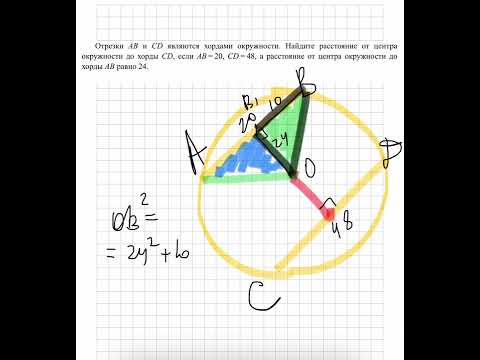 |

 (1)
(1)





