Две окружности касаются в точке к прямая проходящая через

Видео:Геометрия Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второйСкачать

Ваш ответ

Видео:ЕГЭ задание 16Скачать

решение вопроса

Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,044
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Геометрия Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходитСкачать

Две окружности касаются в точке к прямая проходящая через

Две окружности касаются друг друга внешним образом в точке A. Прямая, проходящая через точку A, пересекает первую окружность в точке B, а вторую — в точке C. Касательная к первой окружности, проходящая через точку B, пересекает вторую окружность в точках D и E (D лежит между B и E). Известно, что AB = 5, AC = 4. Точка O — центр окружности, касающейся отрезка AD и продолжений отрезков ED и EA за точки D и A соответственно.

а) Докажите, что

б) Найдите длину отрезка CE.

Центр вписанной в угол окружности лежит на биссектрисе угла. Для решения задачи докажем следующую лемму.

Лемма: точка O принадлежит стороне AB, то есть AB является биссектрисой угла DAF.

Доказательство: во-первых, из свойств секущих к окружности получим:

Тогда треугольники ABD и EBC подобны (угол ABD общий). Тогда ∠BDA = ∠BCE = β, ∠BAD = ∠BEC = γ.

Во-вторых, угол между дугой и касательной равен вписанному углу, опирающемуся на данную хорду, откуда ∠BFA = ∠ABD = α.

Далее, центральный угол AO₂B в 2 раза больше вписанного угла AFB, поэтому Так как треугольник AO₂B равнобедренный (AO₂ = O₂B = R₁), то

Аналогично для угла ACE:

Углы и равны, как вертикальные, и потому получаем:

Отсюда получаем, что а значит точка O лежит на стороне AB. Лемма доказана.

Из леммы получили:

Тогда и треугольники AEC и EBC подобны по 2-м углам, откуда выпишем соотношения:

Из равенства первой и третьей дробей получим:

Тогда

Проведем дополнительно отрезок EO — он является биссектрисой угла BEA, а значит и биссектрисой треугольника ABE. Тогда по свойству биссектрисы в треугольнике имеем:

Критерии оценивания выполнения задания	Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б.	3
Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки.	2
Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Видео:две окружности касаются внешним образом в точке КСкачать Задание 16 Профильного ЕГЭ по математике. Планиметрия. Задача 3 Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C а) Докажите, что прямые AD и BC параллельны. б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1. а) Другими словами, в пункте (а) надо доказать, что точка D лежит на прямой , а точка C — на прямой . — прямоугольная трапеция, поскольку (как радиусы, проведенные в точку касания), . Если , то (как односторонние углы), Тогда — диаметр первой окружности; — диаметр второй окружности, так как вписанный угол, опирающийся на диаметр, — прямой. AK — высота в , где Рассмотрев прямоугольную трапецию , где , найдем, что . 🎦 Видео Задача. Две окружности касаются внутренним образом.Скачать Поступайте правильно Математика ЕГЭСкачать 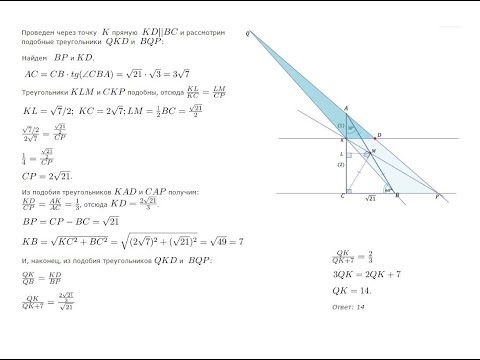10.16.1. Планиметрия. Гордин Р.К.Скачать ЕГЭ Задание 16 Две окружностиСкачать ЕГЭ Задание 16 Две касающиеся окружностиСкачать 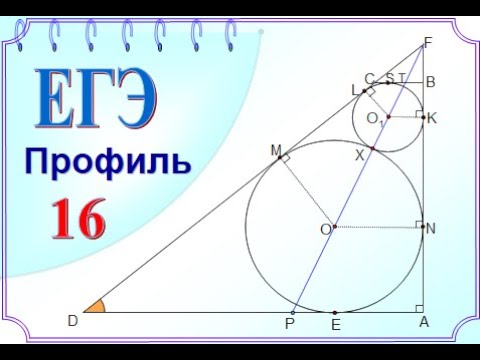ЕГЭ 2022 Профиль 16 задание. ДемоверсияСкачать Две окружности/ Повторяем углыСкачать ЕГЭ Задание 16 Две окружностиСкачать ПЛАНИМЕТРИЯ ЕГЭ | 16 задача из 1 варианта Ященко 2021 🔴Скачать Три окружности касаются прямой и друг друга внешним образомСкачать ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать Демо ЕГЭ по математике. Задача №16Скачать ЕГЭ Задание 16 Три окружностиСкачать №675. Стороны угла О касаются каждой из двух окружностей, имеющих общую касательную в точке АСкачать 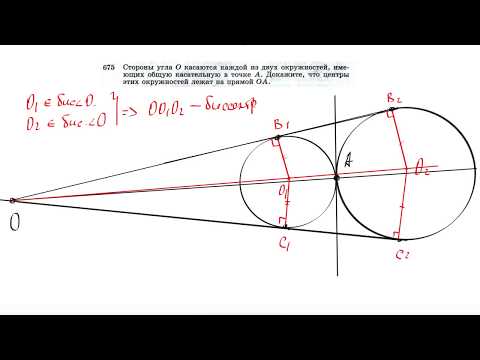Задание 26 Две окружности, внешнее касаниеСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности