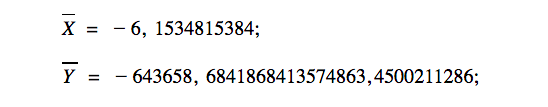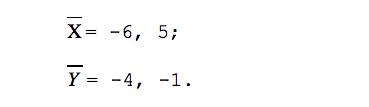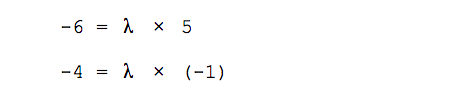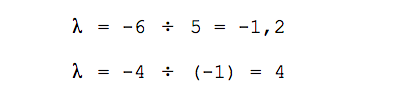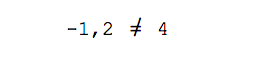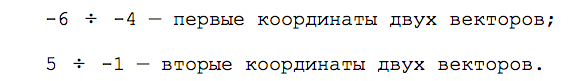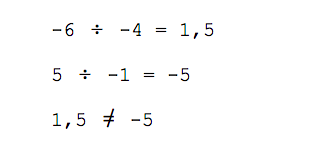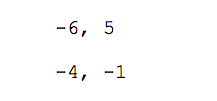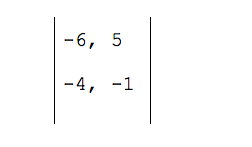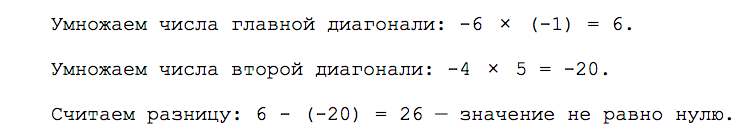Два или несколько векторов совпадают друг с другом artcam

Самопересечение векторов — с данной проблемой сталкивался любой опытный пользователь. ArtCam достаточно капризная программа. Она не позволит нам создать траекторию обработки по вектору, если вектора самопересекаются.

Как же исправить данную проблему?
Рассмотрим несколько примеров:
1. Очевидные варианты — например, когда в вашем векторе есть петли.

Есть 2 решения: убрать петлю (отрезать), либо разбить вектор на 2 штуки — верхний замкнутый и нижний замкнутый вектор.

2. В ситуация, где на глаз не видно ошибку — используем инструмент «Лечение векторов» (выглядит как зеленый плюсик).

Жмем «Обнаружить» и красными кружками нам обведут места, где есть самопересечения.

Часто, в таких неочевидных местах точка наслаивается на точку, что можно обнаружить при помощи инструмента «Редактор узлов»

Включаем узлы вектора, и местах, которые обведены — пытаемся раздвинуть точки между собой.

Также есть более автоматизированный способ, который работает с вероятностью 80% 🙂 Особенно, если ошибок вылезет слишком много.
В таком случае необходимо воспользоваться инструментом «Смещение векторов».

Ставим минимальное значение (0,01 или вроде того) и жмем сместить. После этого проверяем на ошибки. Можно повторить несколько раз.

Видео:⛑Диагностика векторов в ArtcamСкачать

Два или несколько векторов совпадают

Видео:Объединить векторы в арткамеСкачать

Самопересечение векторов

Самопересечение векторов — с данной проблемой сталкивался любой опытный пользователь. ArtCam достаточно капризная программа. Она не позволит нам создать траекторию обработки по вектору, если вектора самопересекаются.

Как же исправить данную проблему?
Рассмотрим несколько примеров:
1. Очевидные варианты — например, когда в вашем векторе есть петли.

Есть 2 решения: убрать петлю (отрезать), либо разбить вектор на 2 штуки — верхний замкнутый и нижний замкнутый вектор.

2. В ситуация, где на глаз не видно ошибку — используем инструмент «Лечение векторов» (выглядит как зеленый плюсик).

Жмем «Обнаружить» и красными кружками нам обведут места, где есть самопересечения.

Часто, в таких неочевидных местах точка наслаивается на точку, что можно обнаружить при помощи инструмента «Редактор узлов»

Включаем узлы вектора, и местах, которые обведены — пытаемся раздвинуть точки между собой.

Также есть более автоматизированный способ, который работает с вероятностью 80% 🙂 Особенно, если ошибок вылезет слишком много.
В таком случае необходимо воспользоваться инструментом «Смещение векторов».

Ставим минимальное значение (0,01 или вроде того) и жмем сместить. После этого проверяем на ошибки. Можно повторить несколько раз.

Видео:Самопересекающиеся вектора в ArtCam. Как их победить?Скачать

Векторы: третий уровень сложности

Знакомимся с коллинеарностью.

Для большинства людей искусственный интеллект — это нечто сложное и таинственное. А для математиков это синоним фразы «перемножение матриц». С точки зрения человека, который владеет линейной алгеброй, в искусственном интеллекте нет ничего загадочного.

Мы хотим, чтобы вы тоже смогли понять искусственный интеллект на уровне математики. Для этого у нас идёт цикл статей про линейную алгебру:

Сама тема несложная, но конкретно этот шаг вам ничего не даст в практическом смысле. Но если вам хватит терпения, на базе этих знаний мы уже перейдём к матрицам.

Видео:Компановка незамкнутых векторов в ArtCamСкачать

Что за коллинеарность

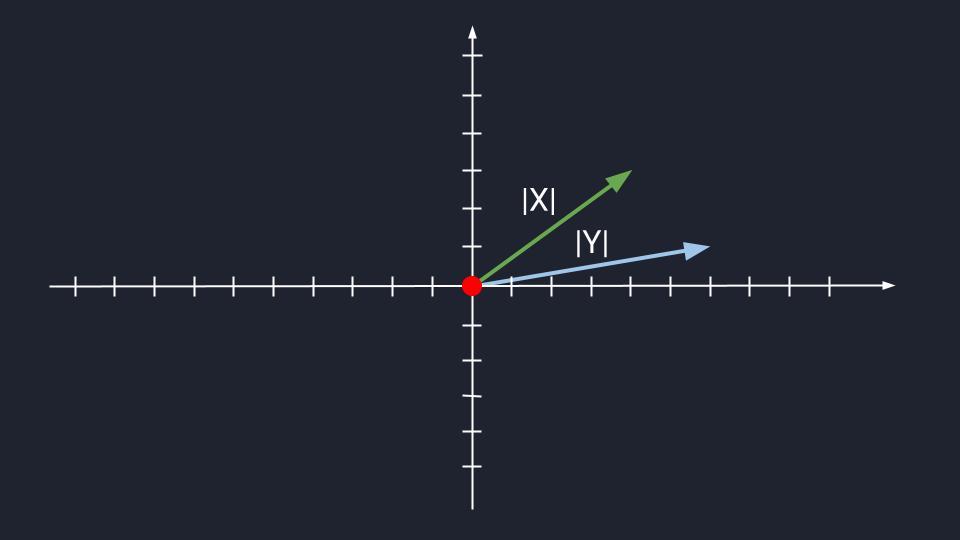
Представьте два вектора, которые находятся в одной плоскости и располагаются параллельно друг другу. При этом у них может быть разная длина. Такое расположение делает связку векторов коллинеарными, или, по-простому, линейно зависимыми.

И наоборот: если вектора находятся в одной плоскости и располагаются не параллельно друг относительно друга, то их считают линейно независимыми — неколлинеарными. Пока что ничего сложного.

Коллинеарные векторы Неколлинеарные векторы

Видео:"Лечение" векторов в Арткаме.Скачать

Сложение коллинеарных и неколлинеарных векторов

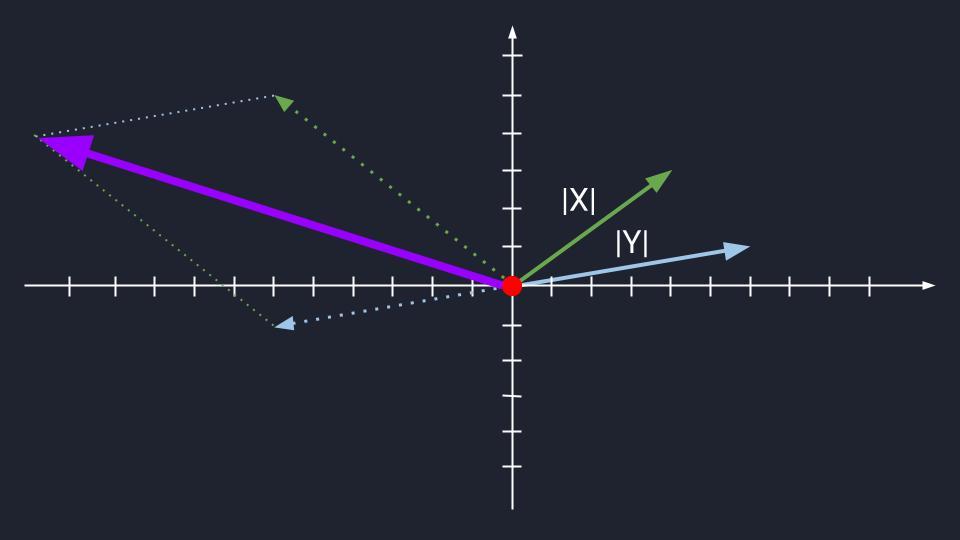
Очевидно, что сложить два коллинеарных вектора очень легко: откладываем второй вектор от начала первого, получится новый вектор. Он будет коллинеарным своим слагаемым, они все будут лежать, грубо говоря, на одной линии.

Можно представить, что вы идёте прямо: каждый ваш шаг — это вектор. Каждый новый шаг — новый вектор. Но если все их сложить, получится один большой прямой вектор длиной как все ваши шаги.

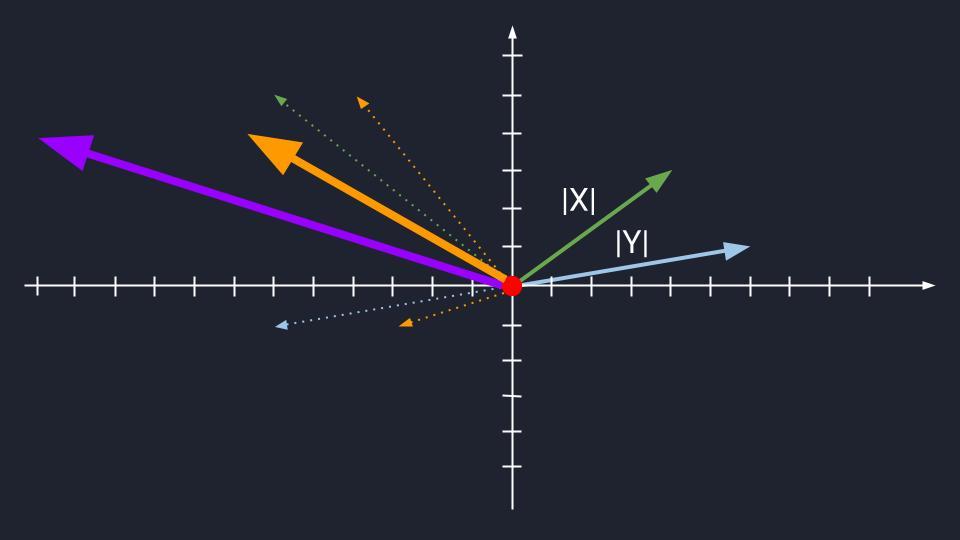
Теперь попробуем сложить пару неколлинеарных векторов. Это как если бы мы сначала сделали шаг немного правее, а потом сделали бы шаг влево. Шага два, но если соединить начало и конец пути, он не будет совпадать с траекториями наших шагов. Появится какой-то новый вектор, с новым направлением, и он будет неколлинеарным по отношению к своим слагаемым.

Также пару неколлинеарных векторов из одной плоскости можно растянуть и развернуть в пространстве. Если их сложить, также появится новый вектор.

У математиков такой вектор называют базисом. Когда базис находится на плоскости или в пространстве, то он может единственным образом превращаться обратно в пару неколлинеарных векторов, которые его сформировали.

Правило работает, когда мы масштабируем и меняем расположение векторов в пространстве. Если мы изменим направление исходных векторов, то получим новый базис.

Базис — понятие из высшей математики, поэтому, если сейчас сложно, не отчаивайтесь. Студенты-математики когда-то тоже отчаивались.

Мы изменили пару неколлинеарных векторов и сформировали из них базис — получили новый фиолетовый вектор с собственной системой координат Теперь мы изменили исходные неколлинеарные векторы и получили новый базис — это оранжевый вектор

Видео:Как справится с наложением векторов друг на друга в программе CorelDRAWСкачать

Как определять неколлинеарность

Когда мы работаем с короткими векторами, всё очевидно: нарисовали систему координат, отложили на ней векторы, они либо совпали, либо не совпали. Если совпали — коллинеарные, если нет — неколлинеарные.

А теперь представьте, что вектора настолько огромные, что мы физически не можем их нарисовать и сопоставить. Например,

Как такое нарисовать? Как проверить коллинеарность? Вот тут начинается магия алгебры.

Есть три способа проверки линейной зависимости векторов. Для простоты вычислений проверим эти три способа на вот этих всё ещё простых векторах:

По этим координатам ответим на два вопроса: являются ли предложенные вектора линейно зависимыми (то есть коллинеарными) и можно ли их раскладывать по базису.

Первый способ. Запишем простую систему уравнений: возьмём первую координату каждого вектора и приравняем её ко второй координате каждого вектора, умноженной на неизвестное число λ. Вычислим λ и сравним результаты.

👉 Знак λ здесь по традиции и для удобства. На самом деле это просто некое неизвестное число. Вместо этой буквы могли быть X, Y, Z или N, но так как у нас вектора уже называются X и Y, а N в математике используется для других целей, возьмём λ — это греческая буква «лямбда», давний предок нашей русской буквы «Л».

Составляем систему уравнений:

Вычисляем значение λ:

Сравниваем результат и делаем вывод:

Мы получили разное значение для неизвестного числа λ и поэтому наши векторы будут считаться линейно независимыми. Из них можно получить базис.

Если бы значение λ совпало, то мы бы имели дело с линейно зависимыми векторами.

Второй способ. Проверяем координаты векторов на пропорциональность: берём первую координату первого вектора, делим её на первую координату второго вектора. Повторяем это же действие со вторыми координатами: берём вторую координату первого вектора и делим её на вторую координату второго вектора.

Получаем такую пропорцию:

Считаем значение и сравниваем результат:

Равенство не выполняется, и поэтому между векторами нет зависимости.

Третий способ. Используем четыре элемента наших координат для поиска определителя — скалярной величины, с которой мы подробно познакомимся в следующих статьях во время решения матричных уравнений. Сейчас нам не нужны подробности, и для проверки линейной зависимости достаточно формулы.

Записываем в две строки координаты наших векторов:

Переводим координаты векторов в определитель — добавляем с двух сторон вертикальную черту и получаем простую квадратную матрицу размером 2 на 2:

В полученной матрице две диагонали. Числа −6 и −1 образуют главную диагональ; числа −4 и 5 — вторую диагональ. Чтобы найти определитель, нам нужно умножить числа главной и второй диагонали, а затем вычесть их разницу.

Если из координат вектора мы получили определитель и он не равен нулю, то векторы считаются линейно независимыми и подходят для разложения по базису.

И наоборот: нулевой определитель указывает на линейную зависимость векторов.

Видео:Мини - курс "Менажница в ArtCam 2018" Урок №2 Создание и редактирование векторов для обработкиСкачать

Что из этого нужно запомнить

• С точки зрения векторов важно, они сонаправленные или нет. По-другому — они коллинеарны или нет.
• Коллинеарность влияет на то, что можно делать с этими векторами. Например, неколлинеарные векторы можно разложить по базису.
• Базис — это вектор, который можно разложить на те самые неколлинеарные векторы.
• Коллинеарность легко проверяется через уравнения. Строить векторы на координатной плоскости необязательно.

Видео:Арткам 2008 Закрытие векторовСкачать

Что дальше

Следующий шаг — матрицы. Это те самые, которые лежат в основе всех нейронок и искусственного интеллекта. Матрица — это таблица чисел, с которыми можно проводить различные вычисления.

Видео:ArtCam. УП по векторам, часть 2.Скачать

Вектор. Виды векторов.

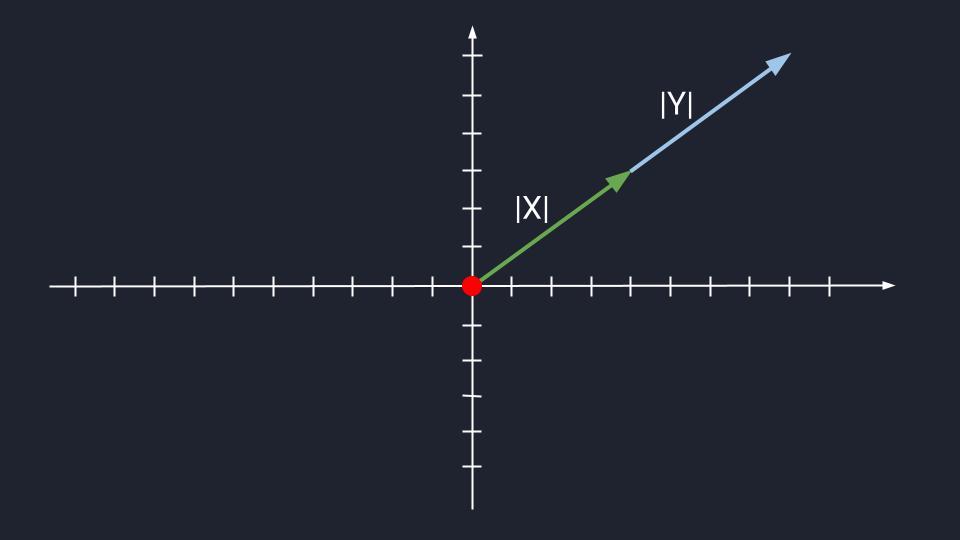
Вектор — в самом элементарном случае это математический объект, который характеризуется

величиной и направлением.

В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая

из его граничных точек является началом, а какая — концом.

У вектора есть длина и определенное направление. Графически вектора изображаются как

направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.

Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Как видно на рисунке, начало отрезка – это точка А, концом отрезка является

точка В, а непосредственно вектор обозначен через . У направления

вектора существенное значение, если переместить стрелку на другую

сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора

удобно сравнивать с движением физического тела: подумайте, ехать на

рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть

разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.

Виды векторов.

Единичным называется вектор, длина которого равна 1.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.

У такого вектора конец и начало совпадают.

Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой

или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются

сонаправленными векторами только тогда, когда их направления

соответствуют друг другу: a↑↑b

Противоположно направленные вектора – два коллинеарных вектора

a и b называются противоположно направленными векторами, только

когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной

плоскости или те, которые лежат на общей плоскости.

В любое мгновение существует плоскость одновременно параллельную

двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на

одной либо параллельных прямых и их направления и длины одинаковые.

То есть, такой вектор можно перенести параллельно ему в каждое место

Таким образом, два вектора равны, если они коллинеарные, сонаправленые

и имеют одинаковые длины:

Для координатного представления векторов огромное значение

оказывает понятие проекции вектора на ось (направленную

прямую).

Проекция вектора — это длина отрезка, который образуется

проекциями точек начала и конца вектора на заданную прямую,

при этом проекции добавляется знак “+”, но когда направление

проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция

вектора на ось, которая перпендикулярна ему = 0.

Когда работают с векторами, зачастую вводят так называемую

декартову систему координат и уже в этой системе находят

координаты вектора по базисным векторам.

Разложение по базису геометрически можно показать проекцией

вектора на координатные оси. Когда известны координаты начала и

конца вектора, то координаты данного вектора получают вычитая

из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как , соответственно

осям x, y, z. Исходя из этого, вектор можно записать в таком виде:

Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование

из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,

кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только

те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).

Видео:artcam работа с векторамиСкачать

ArtCAM. Пример Компоновка векторов (нестинг)

08.12.2012Рассмотрим как произвести компоновку (раскладку) элементов из векторов внутри листа с заданными размерами.

Вы можете скомпоновать выбранные векторы в пределах:

• замкнутой векторной границы, проведенной для представления формы доступного материала; или
• границы области модели ArtCAM; которая представлена в виде белого прямоугольника в окне 2D Вид.

Например, посмотрите, как выглядит векторный текст Nesting Module до и после того, как он был скомпонован в области модели:

В зависимости от выбранных опций компоновки, в модели могут быть созданы следующие объекты:

один или несколько листов, которые добавляются в набор листов в дереве проекта и отображаются в окне 2D Вид.

Листы, созданные в процессе компоновки, содержат скомпонованный векторный эскиз, который не может быть вписан в границы области модели, или вектор, выбранный для представления доступного материала. Однако размеры листа всегда равны области модели.

Чтобы скомпоновать векторы:

1. Откройте панель Компоновка одним из следующих способов:
   • На панели инструментов Создание векторов нажмите на кнопку Компоновать выбранные векторы ; или
   • В Меню выберите Векторы > Компоновать векторы.
2. Если модель ArtCAM не представляет лист или блок материала, в котором вы хотите выполнить компоновку:
   1. На панели Компоновка снимите выделение с опции Использовать модель как границу.
   2. В окне 2D Вид или 3D Вид проведите и затем выберите вектор, представляющий форму доступного материала. Вектор не обязательно должен быть прямоугольником.
   3. Удерживайте нажатой клавишу Shift и выберите каждый из векторов, который вы хотите скомпоновать в пределах уже выбранного вектора.

   По умолчанию векторы компонуются в пределах первого выбранного вектора.

   Если область модели ArtCAM представляет точные размеры вашего материала:

   • На панели Компоновка выберите опцию Использовать модель как границу.
   • В окне 2D Вид или 3D Вид выберите векторный эскиз, который вы хотите скомпоновать в пределах области модели.

   Например, показанный ниже прямоугольник показывает лист материала. Весь выбранный векторный эскиз должен быть сгруппирован в пределах этой области:

   

3. В поле Диаметр (D) введите диаметр режущего инструмента, который вы используете для обработки вложенного векторного эскиза. Это минимальное расстояние, заданное между каждым из скомпонованных векторов.
4. В поле Зазор (C) задайте любое дополнительное расстояние, которое хотите задать между векторами.

   Сумма заданного Диаметра и Зазора равна минимальному расстоянию, заданному между скомпонованными векторами. Чтобы оставить материал между скомпонованными векторами во время процесса обработки, убедитесь, что Зазор больше, чем Диаметр. Это особенно важно, когда траектория, использующаяся для обработки скомпонованного векторного эскиза, включает перемычки для закрепления элементов на месте, или когда вам нужно предотвратить трату материала из-за того, что он перемещается по столу.

   

   

   В поле Отступ по краю задайте отступ от границы области компоновки, которую хотите защитить.

   Обычно он больше или равен Диаметру и добавляется к Зазору, чтобы задать минимальное расстояние между скомпонованными векторами и границей области компоновки.

   Во время процесса компоновки выбранный вами векторный эскиз помещается максимально близко к границе области компоновки; также применяется любой заданный Зазор. В определенных ситуациях вам может понадобиться оставить отступ материала вдоль границы. Например, если вы используете зажимы, чтобы закрепить материал на месте, вам придется обеспечить достаточно места для зажимов, чтобы предотвратить столкновение инструмента с ними.

   Без отступа по краю.

   С отступом по краю.

   

   

5. Чтобы использовать вращение выбранных векторов в процессе компоновки:
   1. Выберите опцию Вращение объектов.
   2. В поле Угол поворота задайте приращение, на которое ArtCAM Express должен их поворачивать.

   Например, если Угол поворота задан как 45 градусов, ArtCAM Express продолжает компоновку векторов, поворачивая их на 0, 45, 90 и 135 градусов по очереди, пока не будет достигнуто наиболее эффективное использование доступного пространства.

   Чем меньше Угол поворота, тем больше свободы дается при организации выбранных векторов. Это дает максимально эффективное использование области компоновки, но увеличивает время вычисления.

   Когда опция Вращение объектов не выбрана, выбранные векторы сохраняют исходную ориентацию в процессе компоновки. Это важно учитывать, когда векторный эскиз должен быть обработан с учетом ориентации зерен материала.

   Без Вращения объектов.

   С Вращением объектов на 20 градусов.

   

   

   Это и остальные опции панели Компоновка предоставляют ArtCAM Express гибкость при вписывании выбранных векторов в доступное пространство.

   Чтобы разрешить отражение векторов в процессе компоновки, выберите опцию Отражение объектов.

   В случае, когда ни одна из ориентаций вектора не вписывается в доступное пространство, вектор отражается, чтобы он вписался. Также как и для вращения объектов, эта опция полезна, когда нужно выполнять обработку с учетом ориентации зерен материала.

   Чтобы векторы были скомпонованы в пределах векторов, включенных в выбранное, с центральной полостью, выберите опцию Размещать Объекты в Объектах.

   Например, буква а помещена в центральную полость буквы О:

   

   Чтобы выровнять векторы по вертикальным или горизонтальным линейным отрезкам в процессе компоновки, выберите опцию Гильотинные резы.

   Гильотинный рез выполняется от одного конца материала к другому. Поэтому при использовании этого метода все выбранные вами векторы должны быть прямоугольными. Однако заданная вами область компоновки не обязательно должна быть прямоугольной.

   Когда выбрана опция Гильотинные резы, новые вертикальные и горизонтальные линейные векторы отображаются в области модели, чтобы обозначить положение каждого гильотинного реза. По умолчанию эти линии показаны зеленым.

   • Если у вас установлен еще и модуль Редактирование векторов, то создается новый векторный эскиз на новом векторном слое Гильотинные резы.
6. В списке Начать с выберите:
   • Нижний Левый, чтобы начать компоновку векторного эскиза из нижнего левого угла границы.

     Например, компоновка векторного текста из Нижнего левого угла вдоль Х выглядит следующим образом:

     

     Нижний Правый, чтобы начать компоновку векторного эскиза из нижнего правого угла границы.

     Например, компоновка векторного текста из Нижнего правого угла вдоль Х выглядит следующим образом:

     

     Верхний Левый, чтобы начать компоновку векторного эскиза из верхнего левого угла границы.

     Например, компоновка векторного текста из Верхнего левого угла вдоль Х выглядит следующим образом:

     

     Верхний Правый, чтобы начать компоновку векторного эскиза из верхнего правого угла границы.

     Например, компоновка векторного текста из Верхнего правого угла вдоль Х выглядит следующим образом:

     

   Нажмите на список Направление, а затем на:

   X, чтобы скомпоновать выбранные векторы вдоль оси Х. Эта опция выбрана по умолчанию.

   Выбор этой опции приводит к тому, что скомпонованные векторы будут расположены горизонтально в пределах заданной границы, вдоль оси Х модели от угла, выбранного в списке Начать с. Например, компоновка векторного текста из Нижнего левого угла вдоль Х выглядит следующим образом:

   

   Y, чтобы скомпоновать выбранные векторы вдоль оси Y.

   Выбор этой опции приводит к тому, что скомпонованные векторы будут расположены вертикально в пределах заданной границы, вдоль оси Y модели от угла, выбранного в списке Начать с. Например, компоновка векторного текста из Нижнего левого угла вдоль Y выглядит следующим образом:

   

7. В поле Точность кривой задайте, насколько близко режущий инструмент должен повторять форму скомпонованного векторного эскиза.
8. Чтобы скомпоновать блок векторного текста или набор векторов, включающий внутренние и внешние части точно так, как они сейчас организованы, то выберите опцию Группировать внутри и снаружи объектов при компоновке.
9. Чтобы определить в выбранном векторы, которые составляют внутренние и внешние части, а затем сгруппировать их, нажмите Сгруппировать.
   • Кнопка Сгруппировать неактивна, если выбрана опция Группировать внутри и снаружи объектов при компоновке.
10. Чтобы создать новый вектор, представляющий форму отходов материала, окружающего сгруппированные векторы:
    1. Выберите опцию Остающийся материал.
    2. Выберите опцию Сохранить в библиотеку, чтобы добавить его в Библиотеку векторов для дальнейшего использования.
    • создается в папке векторных библиотек C:Documents and SettingsAll UsersDocumentsArtCAM FilesVector Libraries;
      • Если вы используете Windows Vista, то библиотека создается в папке C:UsersPublicDocumentsArtCAM FilesVector Libraries. Если вы используете Windows 7, то библиотека создается в папке C:UsersPublicDocumentsArtCAM FilesVector Libraries.
    • называется Отходы раскроя;
    • включает файл Drawing Interchange Format ( *.dxf), содержащий вектор остатков материала для каждого листа скомпонованных векторов; и
      • Размеры вектора остатков материала используются как имя файла DXF. Например, 103291 квадратных мм.
    • включает миниатюрное изображение вектора остатков материала для каждого листа скомпонованных векторов;
    • Чтобы посмотреть свой набор векторов остатков материала, нажмите на кнопку Библиотеки векторов на панели инструментов Создание векторов, а затем выберите Отходы компоновки на панели Библиотека векторов в списке Библиотеки.
11. Чтобы сгруппировать векторный эскиз, назначенный для каждого листа, созданного в процессе компоновки, выберите опцию Сгруппировать вектора.
12. Чтобы сгруппировать несколько копий каждого из выбранных векторов:
    1. В области Несколько копий выберите опцию Все детали.
    2. В поле слева укажите количество копий, которое вы хотите создать.
13. Чтобы скомпоновать заданное количество копий определенного вектора:
    1. Убедитесь, что опция Группировать внутри и снаружи объектов при компоновке не выбрана.
    2. В окне 2D Вид выберите векторы, которые хотите скопировать.
    3. В поле Число деталей укажите количество копий, которое вы хотите создать.
    4. Нажмите Применить. В окне 2D Вид на выбранном векторе отображается число.
14. Чтобы ограничить количество листов в соответствии с количеством имеющегося у вас материала, задайте число листов в поле Макс. кол-во листов.
    • Если вы ограничите количество листов, то ArtCAM Express может не скомпоновать весь выбранный векторный эскиз. Если ArtCAM Express не может скомпоновать все векторы, то отображается сообщение, которое показывает подробности того, сколько векторов было или не было скомпоновано. Все векторные эскизы, которые не были скомпонованы, остаются связанными с Листом по умолчанию и отображаются в исходном положении.
15. Нажмите Компоновать.

    В Строке состояния отображается линейка выполнения, показывающая ход вычисления окончательного положения скомпонованных векторов:

    

    Время вычисления зависит от выбранных опции компоновки. Обычно, чем меньше опций выбрано, тем быстрее процесс компоновки. Вы можете нажать , чтобы остановить процесс компоновки.

    Когда в процессе компоновки создаются листы, каждый лист скомпонованных векторов:

    отображается в окне 2D Вид. Листы располагаются в рядах и колонках; расположение которых изменяется для наиболее экономичного использования рабочего пространства. Несмотря на то, что отображаются все листы, активен только один лист. По умолчанию активен последний созданный лист.

    Например, Лист по умолчанию и четыре листа сгруппированных векторов организованы следующим образом:

    

    добавляется в набор листов в дереве проекта на панели Проект.

    Например, Лист по умолчанию и четыре листа сгруппированных векторов расположены, как показано ниже, и Лист 1 выбран и активен:

    

    По умолчанию активен последний созданный лист. Вы можете отредактировать сгруппированный векторный эскиз на любом листе, но только когда лист активен. Все идентичные листы скомпонованных векторов объединяются в один лист. Например, если обнаруживается, что два листа сгруппированных векторов идентичны первому, то все три листа будут объединены в один лист с именем Лист 1 (3 копии):

    

    В процессе изготовления нужно будет создать только траектории, используя один этот лист, а затем обработать их три раза, чтобы создать необходимое число деталей.

16. Щелкните по в заголовке панели Компоновка, чтобы закрыть ее.

🌟 Видео

#3. Уроки ArtCAM для начинающих. Как создать вектор из картинкиСкачать

Как из картинки извлечь вектор. И сделать 2d модель в Artcam 2018Скачать

Арткам для начинающих. Несколько деталек в одной программеСкачать

ArtCam 2017. Смещение векторовСкачать

Видеоуроки по ArtCam 2018. Компановка векторов.Скачать

Artcam 2018. 2D обработка по векторам.Скачать

Нейрографика не работает?| Нейрографика с Оксаной АвдеевойСкачать

ArtCam. Урок 2 (редактирование векторов).Скачать

Создание управляющей программы в Artcam 2018. Раскрой, выборка, вырезка по векторам.Скачать

2D обработка в ArtCam. Оптимизация обработки.Скачать