Дуга окружности по трем точкам

Не удалось извлечь оглавление

Автор:

Для построения дуги задаются различные комбинации центра, начальной и конечной точек, радиуса, угла, длины хорды и направления.

По умолчанию дуги рисуются в направлении против часовой стрелки. Чтобы нарисовать дугу в направлении по часовой стрелке, необходимо перетаскивать курсор, удерживая нажатой клавишу CTRL.

Видео:Построение окружности по трём точкам.Скачать

Построение дуг по трем точкам

Имеется возможность построения дуги путем задания трех точек. В следующем примере начальная точка дуги совпадает с конечной точкой отрезка. Вторая точка дуги привязана к средней окружности.

Выберите вкладку «Главная» > панель «Рисование» > раскрывающееся меню «Дуга» > «3 точки» . найти

Видео:Построение окружности по трем точкамСкачать

Построение дуги по началу, центру и концу

Имея начальную точку, центр и третью точку, которая определяет конечную точку, можно построить дугу.

Расстояние между начальной точкой и центром определяет радиус. Конечная точка определяется линией из центра, проходящей через третью точку.

Различные параметры позволяют указать вначале начальную точку, а затем центральную, или наоборот.

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Начало, центр, конец» . найти

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Центр, начало, конец» . найти

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Построение дуги по началу, центру и углу

Построить дугу можно с помощью начальной точки, центральной точки и центрального угла.

Расстояние между начальной точкой и центром определяет радиус. Другой конец дуги определяется с помощью задания центрального угла, в котором в качестве вершины используется центр дуги.

Различные параметры позволяют указать вначале начальную точку, а затем центральную, или наоборот.

Положение конечной точки определяется центральным углом. Если же известны начало и конец, но неизвестен центр дуги, следует воспользоваться методом «Начало, конец, угол».

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Начало, центр, угол» . найти

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Центр, начало, угол» . найти

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Начало, конец, угол» . найти

Видео:Как найти центр окружности по трём точкамСкачать

Построение дуги по началу, центру и длине хорды

Построить арку можно с помощью начальной точки, центра и длины хорды.

Расстояние между начальной точкой и центром определяет радиус. Другой конец дуги определяется с помощью задания длины хорды между начальной и конечными точками дуги.

Различные параметры позволяют указать вначале начальную точку, а затем центральную, или наоборот.

Длина хорды определяет центральный угол дуги.

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Начало, центр, длина» . найти

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Центр, начало, длина» . найти

Видео:Математика. Центр окружности по трем точкамСкачать

Построение дуги по начальной точке, конечной точке и углу

Построить дугу можно с помощью начальной точки, конечной точки и центрального угла.

Центральный угол между конечными точками дуги определяет центр и радиус дуги.

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Начало, конец, угол» . найти

Видео:Построение окружности по 3 точкамСкачать

Построение дуги по началу, концу и направлению

Построить дугу можно, имея начальную точку, конечную точку и направление касательной в начальной точке.

Направление касательной можно задать с помощью указания точки на требуемой касательной линии или с помощью задания угла. Можно определить, какая конечная точка управляет касательной, изменив порядок, заданный для двух конечных точек.

Видео:Радиус и диаметрСкачать

Построение дуги по началу, концу и радиусу

Построить дугу можно с помощью начальной точки, конечной точки и радиуса.

Направление прогиба дуги определяется порядком задания ее конечных точек. Радиус можно задать с помощью ввода значения или с помощью указания точки на определенном расстоянии от центра.

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Начало, конец, радиус» . найти

Выберите вкладку «Главная» > панель «Рисование» > раскрывающийся список «Дуга» > «Начало, конец, направление» . найти

Видео:Длина дуги окружности. 9 класс.Скачать

Построение смежных касательных дуг и отрезков

Сразу после построения дуги можно приступить к созданию касательной к дуге в ее конечной точке. Далее потребуется задать только длину отрезка.

Сразу же после создания отрезка или дуги можно построить дугу, касательную в конечной точке. Для этого вызовите команду ДУГА и нажмите клавишу Enter в ответ на запрос «Начальная точка». От пользователя в данном случае требуется задать только конечную точку создаваемой дуги.

Видео:Бондарев А.А. - 5. Доклад "О некоторых классах обеспечения неустойчивости"Скачать

Урок №13. Построение дуги окружности. Произвольная дуга, дуга по трем точкам, дуга касательная к кривой.

Программа “Компас 3D” располагает несколькими методами, позволяющими построить дугу окружности различных типов включая произвольную дугу, дугу по трём точкам, дугу касательно к кривой, дугу по двум точкам, дугу по двум точкам и углу раствора. Данная статья ознакомит вас с некоторыми методами, которые позволят получить дугу окружности.

Произвольная дуга окружности.

Для того, чтобы построить произвольную дугу, вам нужно нажать кнопку “Дуга” в панели компакта или найти её в меню сверху, где оно скрыто за командами “Инструменты” – “Геометрия” – “Дуги” – “Дуга”.

С помощью указателя мышки вы сначала можете задать начало дуги и её центральную точку. Также вы сможете ввести положение точки начала дуги в свойственной панели после того, как зададите размеры угла и радиуса или диаметра в нужных пунктах меню. По умолчанию задаются параметры радиуса. Итак, перейдём к постановке дуги, имеющей центр в начале координатной оси. Начальная точка указывается с учётом радиуса в 30 мм и угла в 150 градусов. После ввода данных, вам нужно будет нажать клавишу ввода или переноса.

После этого с помощью курсора или введя значение угла, вы указываете координаты точки, где будет заканчиваться дуга. Например, можем задать угол в 10 градусов.

После нажатия клавиши ввода, дуга будет строиться автоматически.

По умолчанию построение дуги заданно как построение против часовой стрелки. Если вы желаете задать обратное направление, в панели свойств есть отдельный пункт меню, где вы сможете ввести изменения в установки по умолчанию, как на картинке выше.

Дуга по трем точкам.

Для того, чтобы построить дугу с трема точками, вам нужно нажать кнопку “Дуга по 3 точкам”, которая находится в панели компактного меню или же сверху в меню, где нужно последовательно нажать на пункты “Инструменты” – “Геометрия” – “Дуги” – “Дуга по 3 точкам”.

С помощью курсора мыши, вы получите возможность последовательного указания токи, где дуга будет начинаться, точки, через которую дуга должна проходить (такой точкой может быть, например, вершина прямоугольника), а также точки, в которой дуга будет заканчиваться. В данном случае система сможет самостоятельно просчитать координаты центральной точки и радиус дуги.

Дуга касательная к кривой.

Для того, чтобы построить касательную к кривой линии дугу, вам нужно нажать кнопку “Дуга касательная к кривой” в компактной панели, или же в меню сверху, где вам предстоит нажать команды “Инструменты” – “Геометрия” – “Дуги” – “Дуга касательная к кривой”.

Вам нужно задать точку, через которую пройдёт будущая дуга, а также точку, где дуга будет заканчиваться, с помощью курсора мыши. Система способна рассчитать по умолчанию, какими будут радиус и координаты центральной точки дуги. Начало дуги будет лежать в точке соприкосновения.

После того, как вы укажете точки, экран покажет вам фантомные варианты различных возможностей и вариантов построения дуги. Вам нужно будет выбрать тот, который подходит именно вам. Далее вы должны будете зафиксировать данный вариант с помощью курсора. В завершение построения нужно нажать кнопки “Создать объект” и “Прервать команду”.

Если вы знаете радиус, предписанный касательной дуге, у вас есть возможность ввода его в нужное поле панели свойств. К примеру, можем заняться построением дуги касательной к прямоугольнику с радиусом в 50 мм. После того, как вы закончили ввод значений в ячейки, вам нужно нажать клавишу ввода. Экран опять покажет фантомные варианты построения дуг.

Как и раньше, нужно выбрать соответствующий вам вариант и зафиксировать его.

Стоит помнить о том, что не всегда является возможным построение дуги касательной с помощью указания радиуса. О том, что это невозможно, вам сообщит исчезновение всех фантомных вариантов после того, как вы введете желаемый радиус.

Пока что, это всё. Существуют и другие способы построения дуг, которые мы покроем в следующих уроках.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

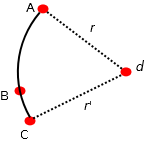
Алгоритм поиска дуги, ее центра, радиуса и углов, заданных 3 точками

даны 3 точки A, B и C

Как я могу найти и дугу, которая начинается на A, заканчивается на C и проходит через B; координаты ее центра, радиус и углы для r и r’ ?

Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

6 ответов

есть несколько способов сделать это. Вот один алгоритм:

получить ваши координаты

вычислить средние точки линий AB и BC

найти наклоны линий AB и До н. э.

построить линии, проходящие через средние точки, перпендикулярные AB и BC (спасибо Ив для ловли отрицательный!)

*** линия с Slope_perp_AB проходит через mid_AB

*** линия с Slope_perp_BC проходит через mid_BC

установите два уравнения равными друг другу и решить, чтобы найти пересечение! Это дает вам точку d= .

вычисление радиуса и углов теперь тривиально с центральной точкой d!

центр круга равноудален от трех заданных точек:

вычитая первый член из второго и третьего, получаем после перегруппировки:

эту линейную систему из двух уравнений в двух неизвестных легко решить с помощью правила Крамера.

радиус и углы можно найти, используя декартово-полярное преобразование вокруг центра:

но вы все еще пропускаете одну вещь: что такое соответствующая часть дуги ? Меньше или больше половины оборота ? От Ta to Tb или Tb до 2 Pi to Ta + 2 Pi , или что ? Ответ гораздо менее очевиден ,чем кажется, попробуйте (потому что три угла Ta , Tb и Tc несколько undeterminate кратного 2 Pi и вы не можете сортировать их) !

подсказка: рассмотрим знак площади треугольника ABC, точно половину определителя системы. Он скажет вам, если B лежит слева или право переменного тока.

найти перпендикуляр AB и BC.

найдите точку, в которой пересекаются эти линии.

точка, которую вы найдете, будет центром круга, который вы хотите.

вычислить расстояние от одной из трех точек от центра, который вы нашли на Шаге 2. Это будет радиус твоего круга.

Примечание точки A, B и C не должны будьте в одной линии. Вы должны проверить это, прежде чем выполнять шаги с 1 по 3.

решение этого почти идентично «кругу наилучшего соответствия для не-сверх-определенной системы». Так как у вас есть три точки, которые находятся точно на дуге бывшей окружностью с центром в (0,0) (дана) система может быть решена точно, а не требующие наименьших квадратов аппроксимация.

ссылки

1. поиск центра круга с учетом трех точек, по состоянию 2014-04-01,

у вас есть три уравнения для определения трех неизвестных xM, yM и R,

etc. Вычитание уравнения A из уравнений B и C дает

решая эту линейную систему 2×2, вы получаете центральную точку круга, вставка в любое исходное уравнение дает радиус.

существует малоизвестный результат, дающий неявное уравнение круга через 3 точки:

где мы определили Z:= X^2 + Y^2 для краткости.

вычисляя 3×3 несовершеннолетних, мы превращаемся в:

и после нормализации получаем обычное уравнение второй степени:

это можно переписать как:

немедленно дать центр (U, V) = (-M10/2.M00, -M20/2.M00) и радиусом R^2 = U^2 + V^2 — M30/M00 .

🔍 Видео

Нахождение центра окружности по 3-м точкам в AutoCADСкачать

КОМПАС 3D - [Дуга по трём точкам]Скачать

Как искать точки на тригонометрической окружности.Скачать

КОМПАС 3D - [Окружность по трём точкам]Скачать

Деление окружности на 3 равные частиСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Дуга по двум точкам и радиусуСкачать

10 класс, 11 урок, Числовая окружностьСкачать