Дуга называется если отрезок соединяющий ее концы является диаметром окружности (2 видео)

Окружность и круг

Содержание

теория по математике 📈 планиметрия
Определения
Свойство хорд
Длина окружности
Дуга, касательная, круг, сектор, сегмент
Свойства касательной
Геометрия. 8 класс
Г р а д у с н а я м е р а д у г и о к р у ж н о с т и. Ц е н т р а л ь н ы й у г о л. — презентация
Похожие презентации
Презентация на тему: » Г р а д у с н а я м е р а д у г и о к р у ж н о с т и. Ц е н т р а л ь н ы й у г о л.» — Транскрипт:
🌟 Видео

теория по математике 📈 планиметрия

Определения

Окружность – множество всех точек плоскости, равноудаленных от одной данной точки (центра окружности). Другими словами – это замкнутая линия, длину которой можно измерить.

На рисунке центр окружности обозначен точкой О. 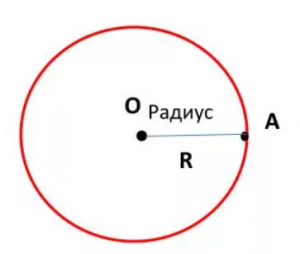Определения

Радиус – расстояние от центра до любой точки окружности. На рисунке радиус обозначен АО. Все радиусы одной окружности равны. Радиус можно обозначать латинскими буквами R или r.

Диаметр – отрезок, который соединяет две точки окружности и проходит через её центр. На рисунке диаметр обозначен АВ. Все диаметры одной окружности равны. В одном диаметре содержится два радиуса. Диаметр обозначается буквой d.

Хорда — длинный эластичный продольный тяж у хордовых животных; осевой скелет их предковых и некоторых современных форм. Тянется вдоль тела ниже центральной нервной системы и выше полости тела.

Свойство хорд

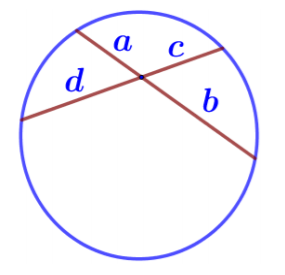
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Так, на рисунке показаны две пересекающиеся хорды, одна состоит из отрезков a и b, вторая из отрезков d и с, следовательно, ab=dс.

Длина окружности

Длину окружности можно вычислить по формуле:

C=2πR, где π=3,14.

Дуга – часть окружности, которая соединяет две точки. На рисунке мы видим несколько дуг, например, дуги CD (малая и большая). Дуга АВ – называется полуокружностью, так как стягивает концы диаметра. Обозначается дуга значком ∪АВ.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Дуга, касательная, круг, сектор, сегмент

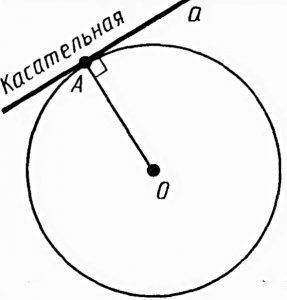
Из точки, не лежащей на окружности можно провести касательную – прямую, которая имеет с окружностью только одну общую точку (рисунок 4).

Свойства касательной

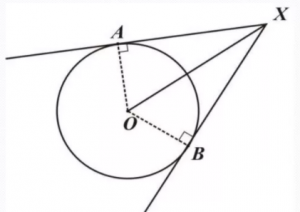
На рисунке видно, что АХ=ВХ, угол АХО равен углу ВХО.

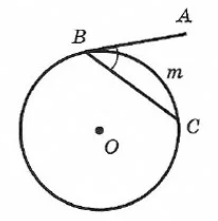
Угол АВС (образован касательной АВ и хордой ВС) равен половине дуги m.

Круг – часть плоскости, ограниченная окружностью. Другими словами, круг – это всё, что находится внутри окружности.

Площадь круга вычисляется по формуле:

S=πR 2 , где π=3,14.

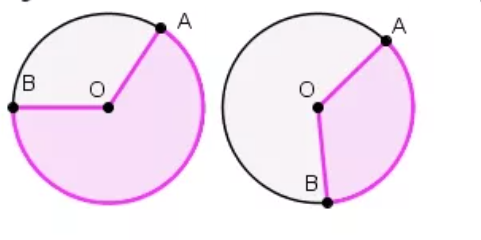
Сектор и его площадь

Сектор – область круга, ограниченная двумя радиусами. На рисунке сектор выделен сиреневым цветом, он ограничен радиусами ОА и ОВ.

Площадь кругового сектора вычисляется по формуле:

S= π R 2 360 . . × α , где α – угол между радиусами.

Сегмент – это область круга, ограниченная хордой и дугой. На рисунке сегмент выделен сиреневым цветом. Также можно сказать, что это часть круга, отсекаемая от него хордой. На рисунке видно, как

Видео:8 класс, 33 урок, Градусная мера дуги окружностиСкачать

Геометрия. 8 класс

Рассмотрим окружность с центром в точке O. Отметим на окружности две точки A и В.

Они разделяют окружность на две дуги. Для того, чтобы различать эти дуги, на каждой из них отмечают промежуточную точку и обозначают дуги тремя буквами.
Например, дуга AСВ и дуга ADB.
∪ ACB и ∪ ADB
Когда понятно, о какой дуге идет речь, то её обозначают двумя буквами.
Например, дуга АС.
∪ АС
Если отрезок, соединяющий концы дуги, является диаметром окружности, то дуга называется полуокружностью.
Любой диаметр делит окружность на две полуокружности.
Рассмотрим угол, вершина которого находится в центре окружности.

Дадим определение: Угол с вершиной в центре окружности называется её центральным углом.
Центральному углу NОM соответствуют две дуги с концами N и M.
Центральный угол может быть развернутым и неразвернутым. Если центральный угол развернутый, то ему соответствуют две полуокружности.

∠NOM — центральный угол
Если центральный угол неразвернутый, то дуга, расположенная внутри этого угла меньше полуокружности. На рисунке эта дуга выделена цветом.

Про другую дугу, соответствующую центральному углу говорят, что она больше полуокружности. На рисунке это дуга NKM.

Дугу окружности можно измерять в градусах.
Если дуга MN окружности с центром в точке O равна полуокружности или меньше полуокружности, то её градусная мера считается равной градусной мере центрального угла NOM.

∪ NKM = 180° ∪ NM = ∠NOM ∪ NKM = 360° — ∠NOM
Если дуга MN больше полуокружности, то ее градусная мера считается равной разности 360° и градусной меры ∠NOM.
Таким образом, градусная мера дуги равна градусной мере соответствующего центрального угла или угла, дополняющего центральный угол до 360°.
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – М.: Просвещение, 2017.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Г р а д у с н а я м е р а д у г и о к р у ж н о с т и. Ц е н т р а л ь н ы й у г о л. — презентация

Презентация была опубликована 6 лет назад пользователемЯна Фролова

Презентация на тему: » Г р а д у с н а я м е р а д у г и о к р у ж н о с т и. Ц е н т р а л ь н ы й у г о л.» — Транскрипт:

1 Г р а д у с н а я м е р а д у г и о к р у ж н о с т и. Ц е н т р а л ь н ы й у г о л.

2 Дуга окружности О А В М N

3 Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности. О А В d

4 А В О Центральный угол Составьте определение центрального угла Угол с вершиной в центре окружности называется центральным углом.

5 А В О Дугу окружности можно измерять в градусах. Если дуга АВ окружности с центром О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ. 85 0

7 А В О Если дуга АВ окружности с центром О больше полуокружности, то ее градусная мера считается равной

9 M А В О Найти,, хорду АВ N 16

10 О п р е д е л е н и е в п и с а н н о г о у г л а

11 А ВС А В Чем похожи и чем различаются углы АОВ и АСВ? О О Центральный угол AOB Вписанный угол ACB Угол с вершиной в центре окружности называется центральным углом. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.С

12 Т е о р е м а о в п и с а н н о м у г л е

13 О А СВ Вписанный угол измеряется половиной дуги, на которую он опирается. 1 случай- 1 случай- центр окружности лежит на одной из сторон углаαα 2a 2α2α2α2α Дано: АВС – вписанный Доказать: Использовано свойство внешнего угла треугольника: Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним

14 О А С В 2 случай – центр окружности лежит внутри угла D+

15 О А С В 3 случай – центр окружности лежит вне угла D–

16 Следствия к теореме о вписанном угле

17 О Вписанные углы, опирающиеся на одну и ту же дугу, равны. Следствие 1 В N M АСF

18 О А СFM N EL S Найдите равные вписанные углы. Ответ обоснуйте.

19 О Вписанный угол, опирающийся на полуокружность – прямой. Следствие 2 ВN MА С F

20 Применение полученных знаний в задачах

21 А С В Найдите градусную меру угла АВС О 55 0

22 А С В Найдите градусную меру угла АВС О

23 Найдите градусную меру угла АВС. О В А С

24 А D В Найдите градусную меру угла АВС О С А можно по- другому!? 40 0 Ученик рассуждал так…

25 А D В Найдите градусную меру угла АВС С О