Дополнительные построения в окружности (6 видео)

Дополнительные построения в планиметрии

Содержание

Задачи с окружностями
Задачи с несколькими вариантами дополнительного построения
Задачи с разрозненными данными
Метод вспомогательной окружности. 9-й класс
Статья по математике «Метод вспомогательной окружности.»
«Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
🎥 Видео

Задачи с окружностями

С помощью дополнительного построения окружности часто решаются задания № 24 и № 26 ОГЭ, а также № 16 ЕГЭ.

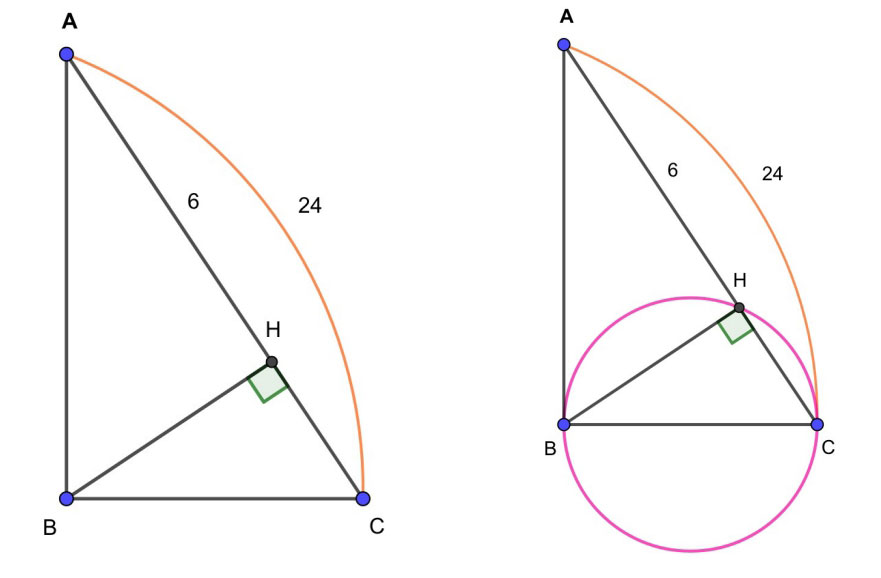
Точка H является основанием высоты, проведенной из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.

Строим окружность вокруг треугольника ВНС. Центр этой окружности является и серединой ВС. ВС — диаметр. АС по отношению к данной окружности — секущая. АВ — отрезок касательной. АН — внешняя часть секущей. Все это подводит к теореме о квадрате касательной.

АВ 2 — произведение секущей на ее внешнюю часть. Следовательно, нужно умножить AH на AC. 6×24 = 144 (это АВ в квадрате). АВ=12. Больше заданий для подготовки к ОГЭ вы найдёте в учебнике «Геометрия. 9 класс».

Задачи с несколькими вариантами дополнительного построения

В условиях задания № 16 ЕГЭ пункт «б» может подсказать, какое решение задачи будет более удачным.

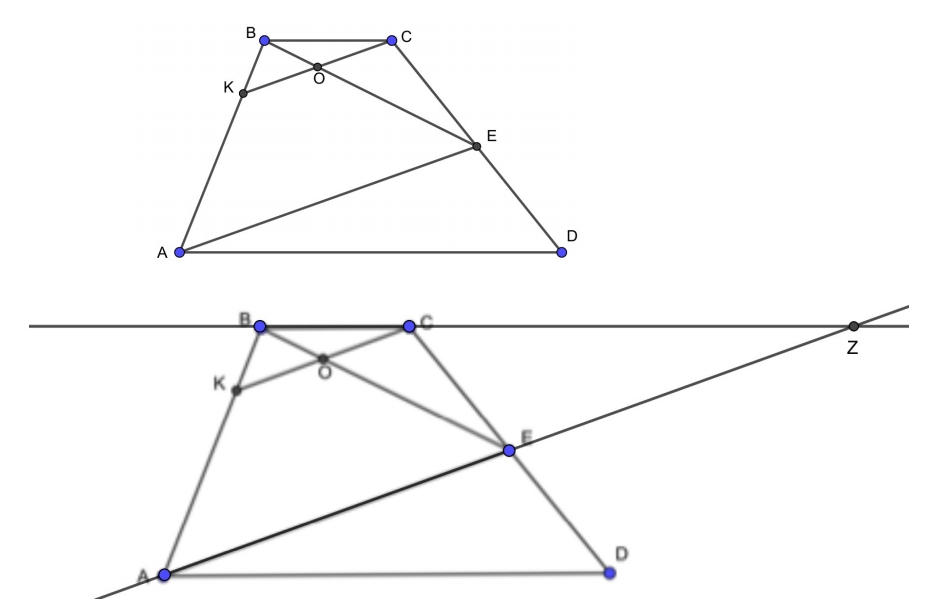
Точка E — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.

а) Докажите, что CO=KO.

б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9/100 площади трапеции ABCD.

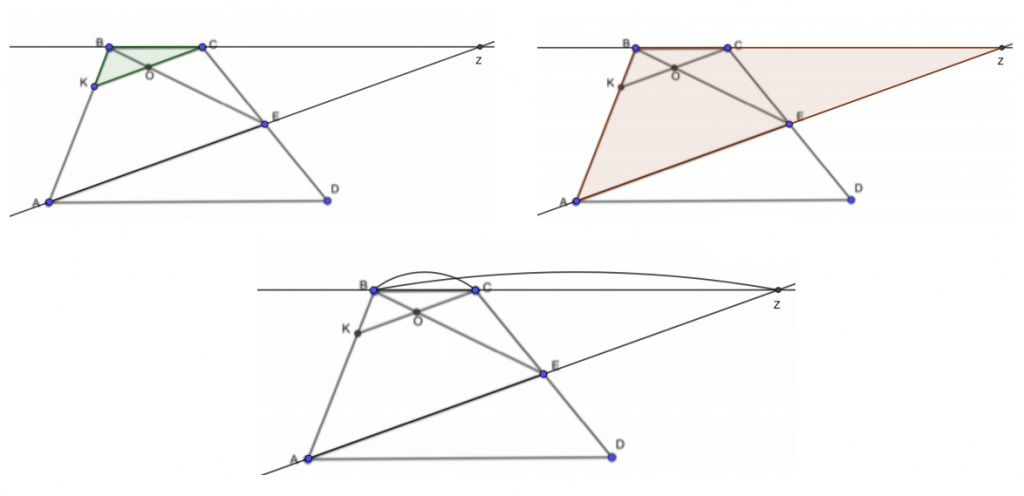
Первый вариант построения. Продлеваем ВС и АЕ, вследствие чего появляются равные треугольники АЕD и ZЕC. Так как АЕ=EZ, то ВЕ — это медиана треугольника АВZ. КС и АZ параллельны. Медиана хороша тем, что она делит пополам не только сторону треугольника, но и любой отрезок, который этой стороне параллелен. Поэтому CO=KO.

Площадь треугольника ABZ такая же, как площадь трапеции ABCD за счет равенства треугольников АЕD и ZЕC. Треугольник КВС подобен треугольнику ABZ. Как известно, отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Отрезок BC, деленый на отрезок BZ, равен 3:10. На отрезок СZ приходится 7 частей. Ответ в пункте «б»: 3:7.

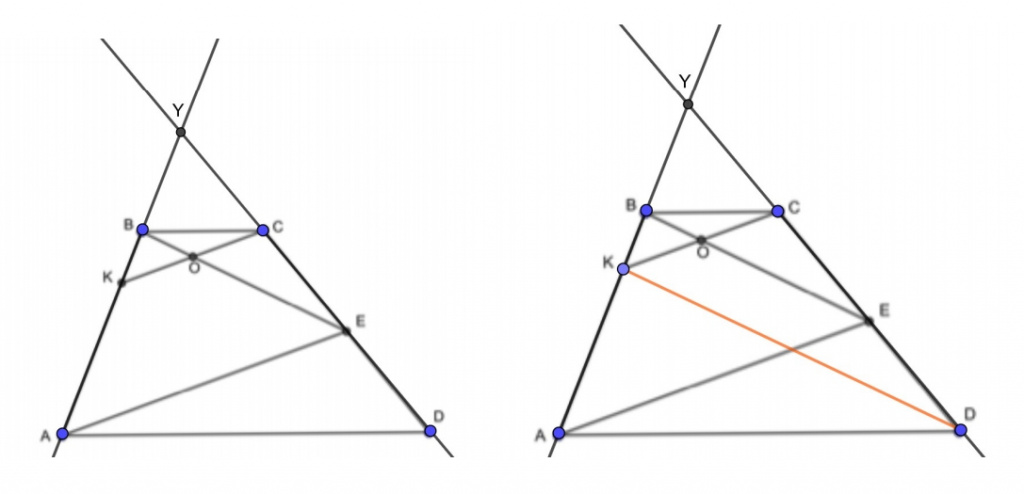
Второй вариант построения. Продолжим стороны AB и CD. Используя теорему, обратную теореме Фалеса, доказываем, что KB относится к BY так же, как YE к ED, и что отрезок KD параллелен BE. В треугольнике KCD видна середина CD. Отрезок OE параллелен KD и проходит через середину — следовательно, является средней линией и проходит через середину KC. Пункт «а» задания выполнен. Разобраться с пунктом «б» при данном дополнительном построении сложнее. К ответу 3:7 приводит то, что KB с BY соотносятся так же, как ED с YE.

Задачи с разрозненными данными

Пример (из всероссийской олимпиады школьников по математике, 8 класс, 2017 год, II этап)

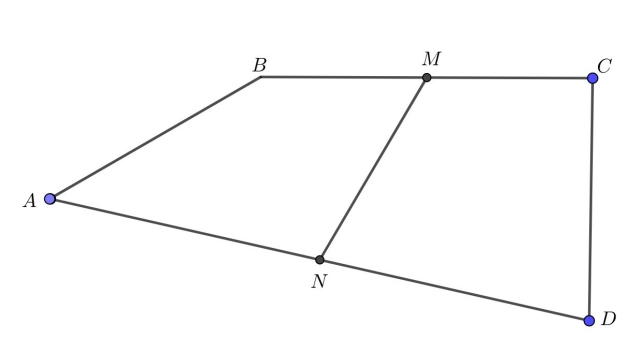
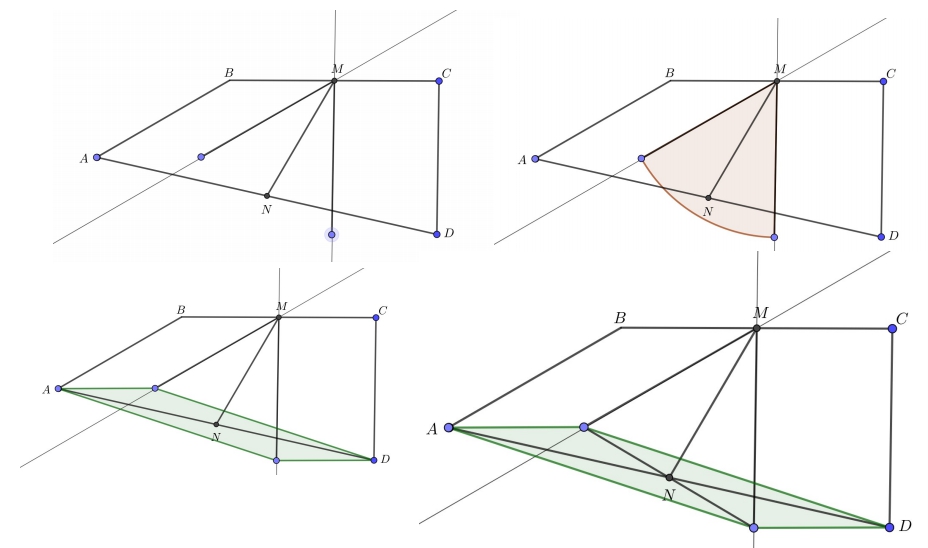
Точки M и N — середины сторон BC и AD четырехугольника ABCD. Известно, что ∠В = 150°, ∠С = 90° и AB = CD. Найдите угол между прямыми MN и BC.

Начинаем компоновку данных с точки М и проводим через нее две прямые, параллельные АВ и CD. Далее от точки М откладываем отрезки, равные АВ и, соответственно, CD. Так получается заготовка для равнобедренного треугольника. Нужно понять, будет ли точка N лежать на отрезке, соединяющем две новые точки. Строятся новые отрезки, равные и параллельные ВМ и МС — получается четырехугольник-параллелограмм. AD является диагональю этого параллелограмма, а N — серединой диагонали. Также N лежит и на другой диагонали. Равнобедренный треугольник готов. Угол с вершиной M в нем равен 60°. Треугольник равносторонний, MN является медианой и биссектрисой. MN, пресекаясь с BC, образует угол, равный 60°.

Чтобы ученики прочно запоминали формулы и теоремы, лучше как можно чаще давать им решать подобные задачи. К слову, задачи с трапециями оптимально подходят для отработки навыка дополнительного построения: две параллельные стороны открывают широкие возможности для создания разных геометрических фигур. Об этом – в учебнике «Геометрия. 7-9 классы».

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Метод вспомогательной окружности. 9-й класс

Разделы: Математика

Класс: 9

Один мудрец сказал “ Высшее проявление духа – это разум, Высшее проявление разума – это геометрия, Клетка геометрии – треугольник. Он так же неисчерпаем, как и Вселенная. Окружность – душа геометрии. Познайте окружность, и вы не только познаете душу геометрии, но и возвысите душу свою”.

Рассмотрим один из основных геометрических методов решения задач – метод вспомогательной окружности. Предлагаю набор задач, который поможет понять и разобраться в этом методе.

При решении некоторых задач может оказаться полезной следующая теорема.

Т.1 Если для четырех точек плоскости А, В, М, К выполняется одно из следующих условий:

а) точки М и К расположены по одну сторону от прямой АВ и при этом 0 , то точки А, В, М, К расположены на окружности с диаметром АВ. (Это свойство вписанных углов сформулированное в более удобном виде для решения задач) Сформулированные выше предложения можно назвать свойства четырех точек окружности.

Т1 и Т2 и свойства вписанных углов позволяют решать некоторые интересные геометрические задачи с помощью метода, который называют методом вспомогательной окружности.

Суть метода проиллюстрируем на решении следующих задач.

В треугольнике АВС проведена высота СК. Найти длину отрезка, соединяющего точку К с серединой АС, если АС = 10см.

Проведем высоту АМ, тогда углы АКВ и АМВ равны по 90 0 , значит точки А, К, М, В лежат на одной окружности и АВ – диаметр.(На рисунке окружность изображена штриховой линией, хотя ее можно и вообще не изображать, а “представлять в уме”) Точка О – середина АС по условию

Следовательно, АО = ОВ = КО = r = 5 см. (рис. 3)

Рис. 3

В выпуклом четырехугольнике АВСD диагонали АС и ВD пересекаются в точке О.

0 , 0 , 0 . Найти углы САD и АDС.

Рис. 4

0 – 49 0 = 62 0 .Таким образом В и С лежат по одну сторону от АD и углы АВО и АСD равны значит точки А, В, С, D лежат на одной окружности. 0 , отсюда 0 – 111 0 = 69 0 .

2. дуга АDС равна 222 0 . Значит дуга DС равна 222 0 – 124 0 = 98 0 . Угол САD вписанный и равен 49 0 . Ответ: 0 0

В окружности проведены параллельные хорды АВ, FC, ED известно, что AD ∩ CE = M,

BE ∩FD = N доказать, что МN ║ АВ.

Обозначим равные дуги АF и ВС – α, тогда , то около четырехугольника ARHQ можно описать окружность, приняв отрезок АН за диаметр. Построив ее, замечаем, что 0 , то точки В, Н, А₁ и С₁ лежат на одной окружности с диаметром ВН. Следовательно, 0 , что и требовалось доказать.

Рис. 8

Рис. 9

б) Рисунок 9 иллюстрирует случай, когда в треугольнике АВС один угол (угол В) тупой. Рассуждение является точно таким же. Только точки В₁ и Н как бы меняются местами. В этом случае точка пересечения высот оказывается расположенной вне треугольника.

Для прямоугольного треугольника точкой пересечения высот является вершина прямого угла.

Таким образом, рассмотренные задачи помогают понять суть метода вспомогательной окружности, использование которого помогает решать геометрические задачи.

И.Ф.Шарыгин. Геометрия Дрофа М.: 2007.
И.Ф.Шарыгин. Решение задач. Просвещение. М.: 2007.

Видео:Две окружности. ОГЭ. Задача 26. Дополнительные построенияСкачать

Статья по математике «Метод вспомогательной окружности.»

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

МЕТОД ВСПОМОГАТЕЛЬНОЙ ОКРУЖНОСТИ .

Геометрия, как учебный предмет, играет огромную роль в развитии познавательной активности и любознательности, логического мышления и пространственного воображения учащихся. Изучение геометрии формирует не только специальные геометрические знания учащихся, но и играет огромную роль в общем развитии личности, ее умении логически мыслить и доказательно обосновывать истинность утверждений в любой сфере деятельности.

Соприкосновение с геометрией носят познавательный, воспитательный, развивающий и вдохновляющий характер. При изучении геометрии и обучении геометрии происходит духовное развитие личности.

Причем хорошее геометрическое образование, пространственное воображение и логическое мышление – необходимые атрибуты не только математика, но и инженера, и экономиста, и дизайнера, и юриста, и программиста, а также специалистов многих других профессий.

Для того, чтобы быстро и успешно справляться с решениями геометрических задач, необходимо владение свойствами ряда опорных геометрических конфигураций, которые часто используются в задачах, умения проанализировать предлагаемую в задачах фигуру, распознать в ней опорную конфигурацию и установить связи между ее элементами.

Все действия, о которых говорилось выше, могут осуществляться только в процессе решения задач. При этом важно уделять внимание геометрическим методам решения задач.

Одним из эффективных методов решения геометрических задач является метод дополнительных построений . Дополнительные построения позволяют свести задачу к другим задачам, решения которых хорошо известны или легко могут быть получены. Требуется большой опыт, изобретательность, геометрическая интуиция, чтоб догадаться, какие дополнительные лини следует провести. Иногда условие задачи подсказывает выбор дополнительного построения.

Одним из дополнительных построений, дающих ключ к решению ряда задач, является проведение вспомогательной окружности. Использование в решении планиметрических задач такого дополнительного построения можно рассматривать как специальный метод решения этих задач – метод вспомогательной окружности.

1. Метод вспомогательной окружности.

Суть метода заключается в том, что при решении планиметрических задач, когда требуется установить связь между данными и искомыми величинами, нередко полезно около треугольника или четырехугольника описать окружность, после чего эти связи становятся более ощутимыми или даже очевидными.

Анализ решения достаточно большого круга задач показывает, что использование вспомогательной окружности связано с характерными признаками фигуры, рассматриваемой в задаче.

Целесообразность применения метода зависит от этих признаков . А они основаны на теоремах и их следствиях, изучаемых в курсе геометрии 8, 9 классов.

Вписанный угол измеряется половиной дуги, на которую он опирается.

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

3) Вписанный угол, опирающийся на полуокружность, прямой.

4) Угол, с вершиной внутри круга, измеряется полусуммой двух дуг, одна из которых расположена внутри этого угла, а другая – внутри угла, вертикального к данному.

5) Угол, вершина которого расположена вне круга, а каждая из сторон пересекает окружность в двух точках, измеряется полуразностью дуг, заключенного внутри угла.

6) Угол между касательной к окружности и хордой, проведенной через точку касания, измеряется половиной дуги, заключенной внутри этого угла.

7) В любой треугольник можно вписать окружность и притом единственную.

Около любого треугольника можно описать единственную окружность.

Из всех параллелограммов только около прямоугольника и квадрата можно описать окружность, центр которой – точка пересечения диагоналей.

Около трапеции можно описать окружность только тогда, когда она равнобочная.

В процессе изучения метода вспомогательной окружности необходимо научиться выделять и использовать те признаки , наличие которых в задаче приводит к построению вспомогательной окружности и с ее помощью устанавливать связи между необходимыми объектами и величинами, определенными условием задачи. Тем более, что задачи на использование метода вспомогательной окружности, частые гости на ЕГЭ и на экзаменах за курс основной школы.

Вот эти признаки.

1) Если дан правильный треугольник, то можно провести окружность с центром в любой из его вершин и радиусом, равным длине его стороны, либо описать около него окружность, которая разобьется вершинами треугольника на равные дуги по 120 0 каждая.

2) Если дан прямоугольный треугольник, то вокруг него описывается окружность, центром которой является середина гипотенузы, а радиус равен медиане, проведенной к гипотенузе этого треугольника.

3) Если удается установить, что суммы противоположных углов выпуклого четырехугольника равны, то вокруг него описывается окружность .

4) Если дан квадрат ,прямоугольник или равнобедренная трапеция, то вокруг них описывается окружность.

5) Пусть около треугольника АВС описана окружность с центром О . Если точки О и С лежат по одну сторону от прямой АВ , то согласно свойству вписанного и центрального углов ; если же эти точки лежат по разные стороны от АВ , то . Обратно, если: 1) точки О и С лежат по одну сторону от АВ , и или 2) точки О и С лежат по разные стороны от АВ , и , то точка О – центр окружности, описанной около треугольника АВС .

6) При определенных условиях окружность можно описать и около четырехугольника. Если четырехугольник ABCD вписан в окружность, то сумма его противоположных углов равна 180 0 , а углы ABD и ACD , опирающиеся на одну и туже дугу, равны (рис. 1). Верно и обратное предложение.

Точки A , B , C , D лежат на одной окружности, если : 1) ABCD – выпуклый четырехугольник и сумма его противоположных углов равна 180 0 или 2) точки В и С лежат по одну сторону от прямой AD и (то есть отрезок AD виден из точек В и С под равными углами).

2. Опорные задачи на метод вспомогательной окружности

Задача 1. В остроугольном треугольнике АВС проведены высоты АА ₁ , ВВ ₁ , СС ₁ . Пусть Н – точка пересечения высот. Постройте треугольник А ₁ В ₁ С ₁ и перечислите все образовавшиеся четырехугольники, около которых можно описать окружность (рис. 2).

Рассмотрим задачи решаемые данным методом.

Задача 2. В остроугольном треугольнике АВС проведены высоты и . Доказать, что треугольник подобен данному треугольнику АВС с коэффициентом подобия, равным .

Решение. На стороне АС треугольника АВС как на диаметре опишем полуокружность, которая пройдет через основания высот и (рис. 3). Так как четырехугольник вписанный, то . Следовательно, и . Так как стороны и являются соответствующими сторонами в подобных треугольниках, то их отношение равно коэффициенту подобия. Но в прямоугольном треугольнике . Итак, и .

Задача 3. Через некоторую точку плоскости проведены три прямые так, что угол между любыми двумя из них равен 60 0 .Докажите, что основания перпендикуляров, опущенных из любой точки плоскости на эти прямые, служат вершинами равностороннего треугольника.

Решение. Пусть три данные прямые пересекаются в точке О ; М – произвольная точка плоскости; А , В , и С основания перпендикуляров, опущенных из точки М на данные прямые (рис. 4). Точки О , М , А , В и С лежат на одной окружности с диаметром ОМ (обоснуйте это). Теперь видно, что , поскольку оба они опираются на одну и туже дугу . Значит, . Точно так же , то есть треугольник АВС равносторонний.

Задача 4. Медиана и высота треугольника, проведенные из одной вершины внутри него, различны и образуют равные углы со сторонами, выходящими из той же вершины. Доказать, что треугольник прямоугольный.

Решение. Пусть высота СН и медиана СМ треугольника АВС образует со сторонами АС и ВС равные углы (рис. 5). Опишем около треугольника АВС окружность. Достаточно доказать, что АВ – ее диаметр. Продолжим медиану СМ до пересечения с окружностью в точке D и рассмотрим треугольники АСН и DCB . Так как по условию и как вписанные углы, опирающиеся на одну и ту же дугу, то . Следовательно, диаметр окружности.

Центр окружности лежит на диаметре и на серединном перпендикуляре m к стороне АВ . Так как по условию CD не является высотой, то прямые m и имеют только одну общую точку М , которая является центром описанной окружности. Следовательно, АВ – диаметр окружности и .

1. Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠ BEC = 120°.

а) Докажите, что ∠ CBE = ∠ COE .

б) Прямая OE пересекает сторону AD прямоугольника в точке K . Найдите EK , если известно, что BE = 40 и CE = 24.

Решение. а) По теореме о внешнем угле

треугольника ∠ BOC = ∠ BAO + ∠ АBO = 2 · 30° = 60°.

∟ ВОС+∟ВЕС=60 ⁰ +120 ⁰ =180 ⁰

Значит, точки B, E, C, O лежат на одной окружности.

Вписанные в эту окружность углы CBE и COE опираются

на одну и ту же дугу, следовательно, ∠ CBE = ∠ COE .

б) По теореме косинусов ВС²=ВЕ²+СЕ²-2ВЕ·СЕ·со s 120 ⁰ ,ВС=56

Вписанные углы BEO и CEO опираются на равные хорды BO и CO , значит, EO — биссектриса угла BEC . Пусть M — точка её пересечения со стороной BC . По формуле для биссектрисы треугольника получаем:

ЕМ=(2ВЕ·СЕ· cos (∟ВЕС/2))/(ВЕ+СЕ)=15

По свойству биссектрисы треугольника СМ/ВМ=СЕ/ВЕ=24/40=3/5, значит,

По теореме о произведении пересекающихся хорд EM · MO = BM · CM , откуда находим, что МО=(ВМ·СМ)/ЕМ=49

Треугольники COM и AOK равны по стороне и двум прилежащим к ней

углам, поэтому OK = OM . Следовательно, EK = EM + 2 OM = 15 + 98 = 113.

2. В остроугольном треугольнике ABC проведены высоты AP и CQ .

а) Докажите, что угол PAC равен углу PQC .

б) Найдите радиус окружности, описанной около треугольника ABC , если известно, что PQ = 8 и ∠ ABC = 60°

Решение. а) Углы APC и AQC — прямые, значит, точки A, Q, P и C лежат на одной окружности с диаметром AC , и, следовательно, равны и вписанные углы PAC и PQC этой окружности, опирающиеся на дугу PC , что и требовалось доказать.

б) Прямоугольные треугольники ABP и CBQ имеют общий угол ABC , следовательно, они подобны, откуда BQ / BP = BC / BA или BQ / BC = BP / BA , но тогда и треугольники BAC и BPQ также подобны, причем коэффициент подобия равен BQ / BP = BC / BA = cosB ,откуда АС= PQ / cosB =8/ cos 60 ⁰ =16 Тогда радиус R окружности, описанной около треугольника ABC равен R = AC / sin 60 ⁰ =16/√3