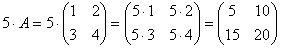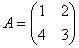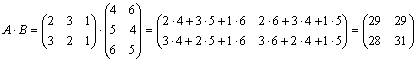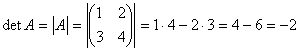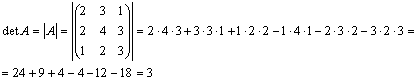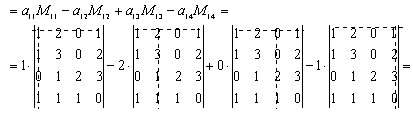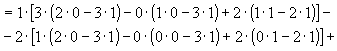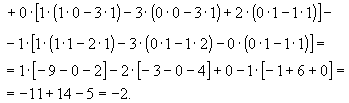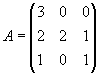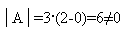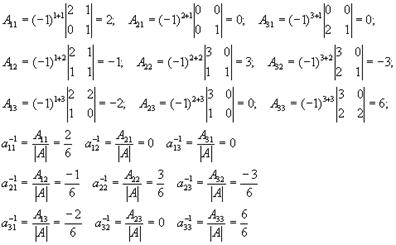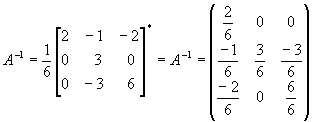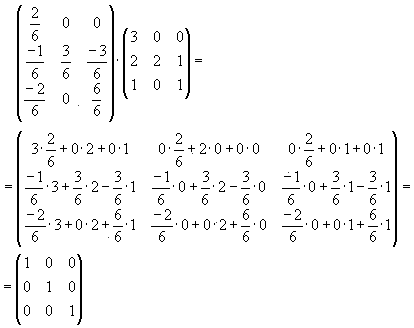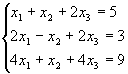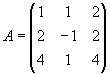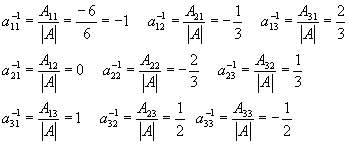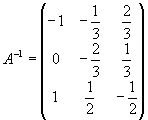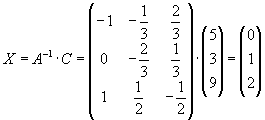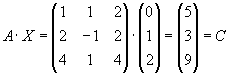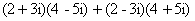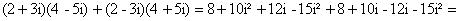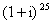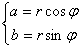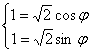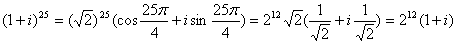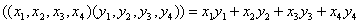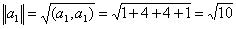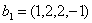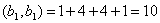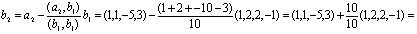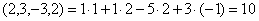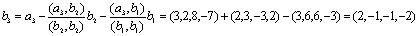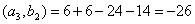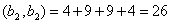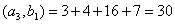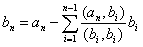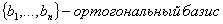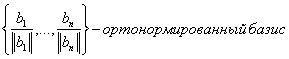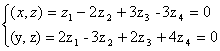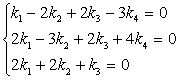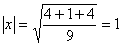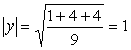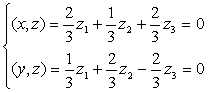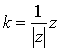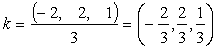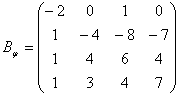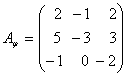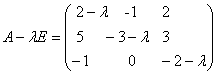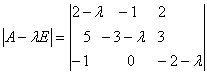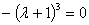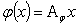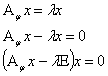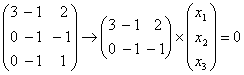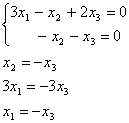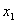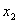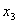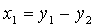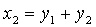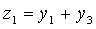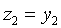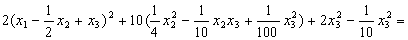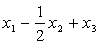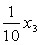Задачи по алгебре. Выпуск 2.
Задача 1. Найти 5А, если
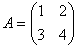
Задача 2. Найти А +В, если
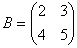
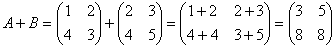
Задача 3. Найти АВ , если
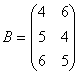
Задача 4. Найти транспонированную матрицу относительно матрицы
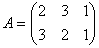
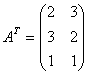
Задача 5. Найти 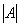
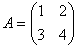
Задача 6. Найти 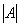
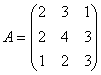
Задача 7. Вычислить определитель
Решение: Разложим определитель по первой строке:
Задача 8. Найти обратную матрицу для матрицы
Определитель нулю не равен, следовательно, обратная матрица существует. Найдем алгебраические дополнения (знаки их учтем сразу), т. е.
Мы сами можем проверить результат, Известно, что 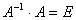
Получилась единичная матрица. Значит, обратная матрица найдена верно.
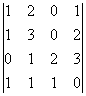
Задача 9. Решить систему матричным способом:
Не является ли матрица А вырожденной? Найдем ее определитель: det А =1•[-1•4 – 1•2] – 1•[2•4 – 2•4] + 2•[2•1 – 4•(-1)] = -6 + 12 = 6
Определитель не равен нулю, то есть матрица не вырожденная. Значит, существует обратная матрица
Можно убедиться проверкой в правильности решения: подставим вектор Х в первоначальное матричное уравнение.
Действительно вектор Х удовлетворяет заданной системе.
Задача 10. Решить систему с помощью формул Крамера :
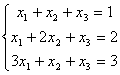
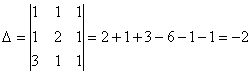
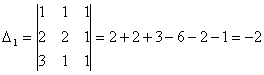
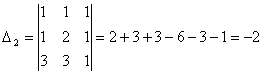
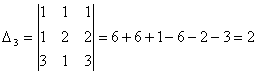
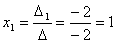
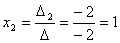
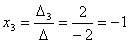
Задача 11. Вычислить :
Раскроем скобки и получим:
Так как 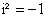
Задача 12. Вычислить, пользуясь формулой Муавра:
Представим число z в тригонометрической форме.
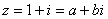
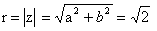
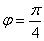
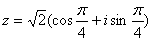
Применим формулу Муавра:
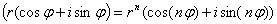
Задача 13. Выполнить деление с остатком f ( x )= x 3 — x 2 — x на x -1+2 i .
Решение: Составим таблицу, в которой над чертой расположены коэффициенты многочлена f ( x ), под чертой соответствующие коэффициенты частного и остаток, последовательно вычисляемые, а слева сбоку – значение c = 1-2 i в данном примере.
Таким образом: f ( x )= x 3 — x 2 — x =( x -1+2 i ) ( x 2 -2 ix -5-2 i )-9+8 i .
Ответ : f(x)=x 3 -x 2 -x=(x-1+2i) (x 2 -2ix-5-2i)-9+8i.
Задача 14. Применяя процесс ортогонализации, построить ортогональный базис подпространства, натянутого на данную систему векторов.
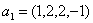
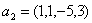
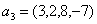
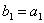
Задача 15. Проверить, что векторы х = (1, -2, 2, -3), у = (2, -3, 2, 4) ортогональны, и дополнить их до ортогональных базисов.
Решение: Найдем скалярное произведение данных векторов: ( х , у) = 2+6+4-12 = 0 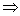
Найдем векторы, дополняющие данную систему векторов до ортогонального базиса.
Пусть z = (z1, z2, z 3, z 4) попарно ортогонален с данными векторами, т.е. ( x , z ) = 0 и ( y , z ) = 0. Получаем следующую систему:
Эта система имеет множество решений, например,
Пусть теперь k = ( k 1, k 2, k 3, k 4) попарно ортогонален с векторами x , y , z . Получаем следующую систему:
Эта система имеет множество решений, например,
Таким образом, можно добавить векторы
(2, 2, 1, 0), (-5, 2, 6, 1).
Задача 16. Найти векторы, дополняющие следующую систему векторов 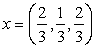
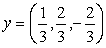
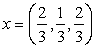
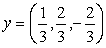
Пусть z = (z1, z2, z 3) попарно ортогонален с данными векторами, т.е. ( x , z ) = 0 и ( y , z ) = 0. Получаем следующую систему:
Эта система имеет множество решений, например,
Нормируя этот вектор, получим вектор, дополняющий данную систему векторов до ортонормированного базиса:
Задача 17. Доказать, что проектирование трехмерного пространства на координатную плоскость натянутую на вектора e 1, e 2 параллельно оси координат вектора e 3, является линейным преобразованием, и найти его матрицу в базисе e 1, e 2, e 3..
Решение: Пусть L — трёхмерное пространство, e 1, e 2, e 3 — базис L , преобразование 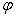
Пусть х — произвольный вектор L , т.е. x Î L .
Пусть x =( x 1, x 2, x 3) — координаты вектора x в базисе e 1, e 2, e 3, т.е. x = x 1 e 1+ x 2 e 2+ x 3 e 3. Тогда при преобразовании j имеем:
Докажем, что для любых x Î L , y Î L и числа l
1) j ( x+y )= j (x)+ j (y),
2) j ( l x )= l j (x).
j ( l x ) = ( l x 1, l x 2, 0) = l ( x 1, x 2, 0) = l j ( x ) .
Следовательно, j — линейное преобразование.
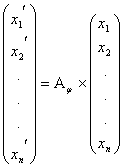
Найдем матрицу преобразования j в базисе e 1, e 2, e 3. Известно, что координаты образа j ( x ) вектора x при линейном преобразовании выражаются через координаты вектора x в том же базисе при помощи матрицы преобразования A j следующим образом:
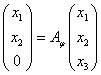
Откуда следует, что
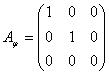
Задача 18. Линейное преобразование φ в базисе е 1 , е2, е3, е4 имеет матрицу
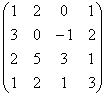
Выпишем матрицу перехода от базиса е 1 ,е2,е3,е4 к новому базису:
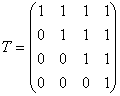
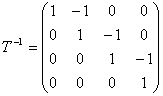
Теперь найдем матрицу преобразования В j в новом базисе по формуле В j =Т -1 А j Т.
Задача 19. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей:
Решение: Собственные значения являются корнями характеристического уравнения преобразования j .
Составим характеристическую матрицу:
Найдем определитель матрицы и вычислим корни характеристического уравнения:
= (2 — 




= 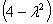
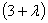


= 12+4 
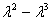

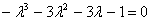
Получим собственные значения: 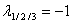
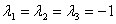
Для каждого собственного значения найдем собственный вектор.
По определению имеем: 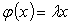
Но, в тоже время,
Беря значением 
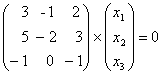

Собственными векторами будут являться вектора, входящие в фундаментальную систему решений (ф.с.р.) этой с.л.а .у . Найдем ф.с.р. это с.л.а .у .
Таким образом, собственным вектором, отвечающим собственному значению 
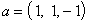
Задача 20. Найти нормальный вид и невырожденное линейное преобразование, приводящее к этому виду, для следующей квадратичной формы: 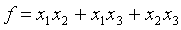
Решение: Ввиду отсутствия в этой форме квадратов неизвестных мы выполним сначала невырожденное линейное преобразование:
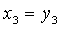
после чего получим 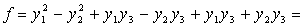
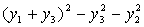
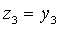
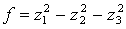
Найдем невырожденное линейное преобразование.
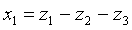
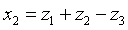
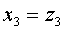
Задача 21. Следующую квадратичную форму привести к каноническому виду с целыми коэффициентами посредством невырожденного линейного преобразования с рациональными коэффициентами и найти выражение новых неизвестных через старые.
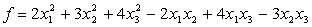
Решение: Приведем данную форму к каноническому виду:
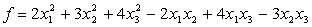
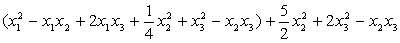
= 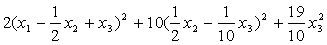
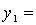
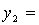
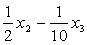
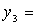
получим канонический вид квадратичной формы:
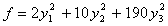
- Ортогональный и ортонормированный базисы евклидова пространства
- Выражение скалярного произведения через координаты сомножителей
- Преимущества ортонормированного базиса
- Изменение матрицы Грама при переходе от одного базиса к другому
- Свойства определителя Грама
- Изоморфизм евклидовых пространств
- Ортогональные системы векторов
- 📹 Видео
Видео:Ортогональные системы векторов. Процесс ортогонализации (задача 1357)Скачать

Ортогональный и ортонормированный базисы евклидова пространства
Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.
Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортогональным , если все образующие его векторы попарно ортогональны, т.е.
Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортонормированным , если его векторы попарно ортогональны и длина каждого из них равна единице:
Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.
В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис.
Видео:Ортогональное дополнение. ПримерСкачать

Выражение скалярного произведения через координаты сомножителей
Пусть [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис евклидова пространства, в котором векторы [math]mathbf[/math] и [math]mathbf[/math] имеют координаты [math]x_1,x_2,ldots,x_n[/math] и [math]y_1,y_2,ldots,y_n[/math] соответственно, т.е.
Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:
Преобразуем это выражение, используя операции с матрицами:
y=begin y_1&cdots& y_n end^T[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] , a [math]G(mathbf_1,mathbf_2,ldots, mathbf_n)[/math] — квадратная симметрическая матрица, составленная из скалярных произведений
которая называется матрицей Грама системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] .
Видео:Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Преимущества ортонормированного базиса
Для ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)[/math] ортонормированной системы [math]mathbf_1, mathbf_2,ldots, mathbf_n[/math] равна единичной матрице: [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)=E[/math] .
1. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] находится по формуле: [math]langle mathbf,mathbfrangle= x_1y_1+x_2y_2+ldots+x_ny_n[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] , а [math]y_1,ldots,y_n[/math] — координаты вектора [math]mathbf[/math] .
2. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] длина вектора [math]mathbf[/math] вычисляется по формуле [math]|mathbf|= sqrt[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] .
3. Координаты [math]x_1,ldots,x_n[/math] вектора [math]mathbf[/math] относительно ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] находятся при помощи скалярного произведения по формулам: [math]x_1=langle mathbf,mathbf_1rangle,ldots, x_n=langle mathbf,mathbf_nrangle[/math] .
В самом деле, умножая обе части равенства [math]mathbf= x_1 mathbf_1+ldots+x_n mathbf_n[/math] на [math]mathbf_1[/math] , получаем
Аналогично доказываются остальные формулы.
Видео:ОртогональностьСкачать

Изменение матрицы Грама при переходе от одного базиса к другому
Пусть [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] и [math](mathbf)= (mathbf_1,ldots,mathbf_n)[/math] — два базиса евклидова пространства [math]mathbb[/math] , a [math]S[/math] — матрица перехода от базиса [math](mathbf)[/math] к базису [math](mathbf)colon, (mathbf)=(mathbf)S[/math] . Требуется найти связь матриц Грама систем векторов [math](mathbf)[/math] и [math](mathbf)[/math]
По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] в разных базисах:
где [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] и [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>,[/math] [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>[/math] , получаем тождество
Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому :
Записав это равенство для ортонормированных базисов [math](mathbf)[/math] и [math](mathbf)[/math] , получаем [math]E=S^TES[/math] , так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf_1,ldots,mathbf_n)= G(mathbf_1,ldots,mathbf_n)=E[/math] . Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^=S^T[/math] .
Видео:Ортогональное дополнение. ТемаСкачать

Свойства определителя Грама
Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.
1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.
Действительно, если система [math]mathbf_1, mathbf_2, ldots,mathbf_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math] , не равные нулю одновременно, что
Умножая это равенство скалярно на [math]mathbf_1[/math] , затем на [math]mathbf_2[/math] и т.д. на [math]mathbf_k[/math] , получаем однородную систему уравнений [math]G(mathbf_1,mathbf_2,ldots,mathbf_k)x=o[/math] , которая имеет нетривиальное решение [math]x=beginx_1&cdots&x_k end^T[/math] . Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.
Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.
Главный минор матрицы Грама системы [math]mathbf_1, mathbf_2,ldots,mathbf_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.
2. Определитель Грама [math]det<G (mathbf_1,mathbf_2, ldots, mathbf_k)>[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] . Другими словами, если в процессе ортогонализации векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] получены векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , то
Действительно, в процессе ортогонализации по векторам [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] последовательно строятся векторы
После первого шага определитель Грама не изменяется
Выполним с определителем [math]det G(mathbf_1, mathbf_2, ldots,mathbf_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_)[/math] , а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_)[/math] . Получим определитель
Так как при этих преобразованиях определитель не изменяется, то
Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:
Вычислим правую часть этого равенства. Матрица [math]G(mathbf_1,mathbf_2,ldots, mathbf_k)[/math] Грама ортогональной системы [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] векторов является диагональной, так как [math]langle mathbf_i,mathbf_jrangle=0[/math] при [math]ine j[/math] . Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:
3. Определитель Грама любой системы [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] векторов удовлетворяет двойному неравенству
Докажем неотрицательность определителя Грама. Если система [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] , для которых по свойству 2:
Оценим теперь скалярный квадрат [math]langle mathbf_j,mathbf_jrangle[/math] . Выполняя процесс ортого-1нализации, имеем [math]mathbf_j= mathbf_j+ alpha_mathbf_1+ ldots+ alpha_mathbf_[/math] . Отсюда
Следовательно, по свойству 2 имеем
1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.
2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.
3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара :
Действительно, обозначив [math]a_1,a_2,ldots,a_n[/math] столбцы матрицы [math]A[/math] , элементы матрицы [math]A^TA[/math] можно представить как скалярные произведения (8.27): [math]langle a_i,a_jrangle= (a_i)^Ta_j[/math] . Тогда [math]A^TA=G(a_1,a_2,ldots,a_n)[/math] — матрица Грама системы [math]a_1,a_2,ldots,a_n[/math] векторов пространства [math]mathbb^n[/math] . По свойству 3, теореме 2.2 и свойству 1 определителя получаем доказываемое неравенство:
4. Если [math]A[/math] — невырожденная квадратная матрица, то любой главный минор матрицы [math]A^TA[/math] положителен. Это следует из пункта 2, учитывая представление произведения [math]A^TA=G(a_1,ldots,a_n)[/math] как матрицы Грама системы линейно независимых векторов [math]a_1,ldots,a_n[/math] — столбцов матрицы [math]A[/math] (см. пункт 3).
Видео:Образуют ли данные векторы базисСкачать
Изоморфизм евклидовых пространств
Два евклидовых пространства [math]mathbb[/math] и [math]mathbb'[/math] называются изоморфными [math](mathbbleftrightarrow mathbb’)[/math] , если они изоморфны как линейные пространства и скалярные произведения соответствующих векторов равны:
где [math](cdot,cdot)[/math] и [math](cdot,cdot)'[/math] — скалярные произведения в пространствах [math]mathbb[/math] и [math]mathbb'[/math] соответственно.
Напомним, что для изоморфизма конечномерных линейных пространств необходимо и достаточно, чтобы их размерности совпадали (см. теорему 8.3). Покажем, что это условие достаточно для изоморфизма евклидовых пространств (необходимость следует из определения). Как и при доказательстве теоремы 8.3, установим изоморфизм n-мерного евклидова пространства [math]mathbb[/math] с вещественным арифметическим пространством [math]mathbb^n[/math] со скалярным произведением (8.27). В самом деле, взяв в пространстве [math]mathbb[/math] какой-нибудь ортонормированный базис [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] , поставим в соответствие каждому вектору [math]mathbfin mathbb[/math] его координатный столбец [math]xin mathbb^n
(mathbfleftrightarrow x)[/math] . Это взаимно однозначное соответствие устанавливает изоморфизм линейных пространств: [math]mathbbleftrightarrow mathbb^n[/math] . В ортонормированном базисе скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] пространства [math]mathbb[/math] находится по формуле
(см. пункт 1 преимуществ ортонормированного базиса). Такое же выражение дает скалярное произведение (8.27) координатных столбцов [math]x[/math] и [math]y[/math] , т.е. скалярные произведения соответствующих элементов равны
Следовательно, евклидовы пространства [math]mathbb[/math] и [math]mathbb^n[/math] изоморфны.
Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]mathbb^n[/math] со стандартным скалярным произведением (8.27).
Видео:Ортогональное дополнение (задача 1366)Скачать
Ортогональные системы векторов
Векторное пространство 



Два вектора 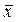


Система векторов 


Базис 



Каждый вектор 






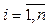
Ортогональной составляющей вектора 




Процессом ортогонализации системы векторов 











1.123 Выяснить будут ли ортогональными следующие системы векторов.
а) 
б) 
в) 
г) 
1.124 Проверить ортогональность систем векторов и дополнить их до ортогональных базисов.
а) 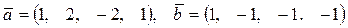
б) 
в) 
г) 
1.125Найти координаты вектора 




1.126 Найти координаты вектора 



1.127 Найти ортогональную составляющую 


а) 
б) 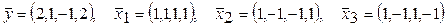
в) 
г) 
В задачах 1.128-1.133 применяя процесс ортогонализации построить ортогональную систему векторов.
1.128 
1.129 
1.130 
1.131 
1.132 
1.133 
Линейные операторы.
Операторомв 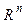
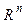
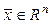
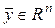


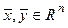


Если 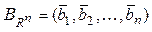



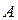





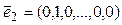






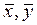
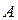


Для линейных операторов вводятся операции: 1) сложение операторов: 


Обратнымк оператору 






Пусть число 
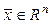


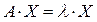


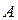










Характеристическим уравнением оператора 


Множество собственных чисел оператора (матрицы) совпадает с множеством корней его характеристического уравнения: 
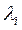

Если квадратная матрица 
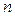






Приведение матрицы 



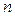



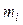
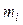



В задачах 1.134-1.138 установить, какие из заданных отображений пространства арифметических векторов 
1.134 
1.135 
1.136 
1.137 
1.138 
В задачах 1.139-1.143 в пространстве 





1.139 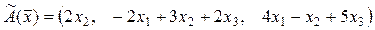

1.140 

1.141 

1.142 
1.143 .
В задачах 1.144-1.146 установить, какие из заданных в 

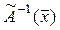
1.144 .
1.145 .
1.146 .
В задачах 1.147-1.156 найти собственные числа и собственные векторы линейных операторов,заданных своими матрицами
1.147 . 1.148 .
1.149 . 1.150 .
1.151 . 1.152 .
1.153 . 1.154 .
1.155 . 1.156 .
В задачах 1.157-1.166 выяснить, какие из заданных матриц линейных операторов можно диагонализировать и найти:
а)диагональную форму матрицы; б) матрицу линейного преобразования, приводящего данную матрицу к диагональному виду.
1.157 . 1.158 .
1.159 . 1.160 .
1.161 . 1.162 .
1.163 . 1.164 .
1.165 . 1.166 .
Квадратичные формы.
Квадратичной формой 

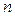


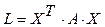




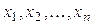
Квадратичная форма называется невырожденной, если её матрица — невырожденная. Квадратичная форма называется канонической, если она имеет вид: 
Всякую квадратичную форму всегда можно привести к канонической, например, методами Лагранжа и ортогональных преобразований.
Метод Лагранжа состоит в последовательном выделении в квадратичной форме полных квадратов. Если в квадратичной форме все коэффициенты 


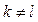

Метод ортогональных преобразований состоит в приведении формы 





Квадратная матрица 


Квадратичные формы подразделяют на различные типы в зависимости от множества их значений. Квадратичная форма 
положительно (отрицательно) определённой, если для любого 











Невырожденная квадратичная форма может быть либо положительно определённой, либо отрицательно определённой, либо знакопеременной. Тип невырожденной квадратичной формы можно определить, проверяя знаки главных миноров матрицы квадратичной формы.
Пусть 








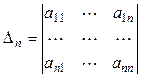
Одним из критериев знакоопределённости невырожденной квадратичной формы является критерий Сильвестра:
— квадратичная форма 
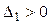



— квадратичная форма 





— квадратичная форма 
1.167 Записать матрицу следующих квадратичных форм:
а) 
б) 
в) 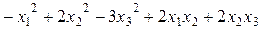
г) 
В задачах 1.168-1.173 методом Лагранжа найти: а) канонический вид квадратичной формы; б) невырожденное линейное преобразование, приводящее к этому виду.
1.168 .
1.169 .
1.170 .
1.171 .
1.172 .
1.173 .
В задачах 1.174-1.179 найти ортогональное преобразование, приводящее следующие квадратичные формы к каноническому виду, и записать полученный канонический вид.
1.174 .
1.175 .
1.176 .
1.177 .
1.178 .
1.179 .
В задачах 1.180-1.185 определить, используя критерий Сильвестра, какие квадратичные формы являются либо положительно, либо отрицательно определенными, а какие нет.
1.180 . 1.181 .
1.182 .
1.183 .
1.184 .
1.185 .
1.186Найти, используя критерий Сильвестра, все значения параметра 
а) 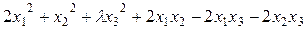
б) 
в) 
Г) .
1.187Найти, используя критерий Сильвестра, все значения параметра 
а) 
б) 
в) 
📹 Видео
§48 Ортонормированный базис евклидова пространстваСкачать

Доказать, что векторы a, b, c образуют базис и найти координаты вектора d в этом базисеСкачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Ортогональность. ТемаСкачать

Как разложить вектор по базису - bezbotvyСкачать

A.7.4 Ортогонализация набора векторов. Процесс Грама-Шмидта.Скачать

Разложение вектора по базису. 9 класс.Скачать

Разложение вектора по векторам (базису). Аналитическая геометрия-1Скачать

Процесс ортогонализации Грама-Шмидта. ПримерСкачать

Найдите разложение вектора по векторам (базису)Скачать

Скалярное произведение. Ортогональный базис.Скачать

Базис линейного пространства (01)Скачать

Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать