Доклад на тему круг и окружность математика 6 класс (2 видео)

Исследовательская работа по математике «Окружность и круг»

Данная тема представляет определенный интерес, так как её истоки относятся к древности. Окружность — самая простая из кривых линий. Это одна из древнейших геометрических фигур, которая всегда привлекала внимание художников, архитекторов. Философы древности придавали ей большое значение.

Содержание

Скачать:
Предварительный просмотр:
Окружность и круг
Определения
Различия
Сходства
Формулы
Окружность и прямая
Окружность и угол
Что мы узнали?
Проект «Окружность и круг»
📽️ Видео

Видео:Окружность и круг, 6 классСкачать

Скачать:

Вложение	Размер
issledovat_rabota_yulya.docx	124.94 КБ

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Предварительный просмотр:

Окружность и круг

Автор: Алексашина Юлия

ученица 5 класса

ГБОУ ООШ №3 г. Жигулевск

Руководители: Царькова Д.А.

ГБОУООШ №3 г.о.Жигулевск

г. Тольятти, 2013

Основная цель работы: исследование окружности и круга.

Основные задачи исследования:

1) познакомиться с понятиями: окружность, центр и радиус окружности, диаметр, хорда окружности.

2) выяснить, на какое наибольшее число частей можно разделить окружность тремя прямыми.

3) выяснить, существует ли круг, чтобы его площадь и длина окружности выражались одним и тем же числом.

4) рассмотреть взаимное расположение на плоскости прямой и окружности.

5) рассмотреть взаимное расположение на плоскости двух окружностей.

Основные методы решения поставленных задач : метод наблюдения за числами; метод подбора и проб; чтение дополнительной литературы; составление таблиц и сравнение результатов; метод обобщения.

Часть 1. Основные понятия, используемые в работе

1.1. Понятие Окружности

Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.

Данная точка (O) называется центром окружности.

Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности.

1.2. Длина окружности

Отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой π («пи»).

Обозначим длину окружности буквой l , а ее диаметр буквой d и запишем формулу

Число π приблизительно равно 3.14

Более точное его значение π = 3,1415926535897932. Исходя из формулы выше, выведем, чему равна окружность, если известен диаметр d .

Если известен радиус r , то формула длины окружности будет выглядеть так:

1.3. Радиус окружности

Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Определить радиус окружности можно по формуле:

1.4. Диаметр окружности

Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Центр окружности является серединой любого диаметра. Определить диаметр окружности можно по формуле:

где R — радиус, D — диаметр, π — число π = 3,14.

Часть 2. Постановка и решение задач

2.1. Постановка первой задачи

Рассмотрим, на какое наибольшее число частей можно разделить окружность тремя прямыми.

Рассмотрев всевозможные варианты, можно сделать вывод о том, что наибольшее число частей, на которое можно разделить окружность тремя прямыми равно 7.

Итак, сделаем первый вывод : наибольшее число частей, на которое можно разделить окружность тремя прямыми равно 7.

2.2. Постановка второй задачи

Дан квадрат, периметр и площадь которого выражаются одним и тем же числом.

Пусть сторона квадрата равна Х, тогда Р=4Х , а S=X 2 .

Таким образом, можно сделать вывод, что при стороне квадрата равной 4, периметр и площадь будут выражаться одним целым числом.

Предположим, что существует круг, площадь и длина окружности которого выражаются одним числом.

Длина окружности вычисляется по формуле: L=2пR=пD

Площадь: S = πR 2 . π=3,14

Составим таблицу 1.

Из таблицы видно, что при радиусе равном 2 площадь и длина окружности, которого выражаются одним числом.

Итак, сделаем второй вывод: существует круг, площадь и длина окружности которого выражаются одним числом, радиус которого равен 2.

2.3. Постановка третей задачи

сравним длины окружностей, заменяя π числами и

Найдем длину окружности, если радиус равен 497 см.

2.4. Постановка четвертой задачи

При вычислении длины окружности в Древнем Вавилоне за π часто принимали число, равное 3. Сравним их ответ от настоящего ответа при нахождении длины окружности. R= 40

Сравнив полученные данные, можно сделать вывод, что при вычислении длины окружности в Древнем Вавилоне ответ меньше настоящего на 11,2.

2.5. Постановка пятой задачи

Рассмотрим всевозможные случаи взаимного расположения на плоскости прямой и окружности.

Если расстояние от центра окружности до прямой меньше радиуса окружности ( d ), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.

Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности .

Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

2.6. Постановка шестой задачи

Рассмотрим всевозможные случаи взаимного расположения на плоскости двух окружностей.

Окружности не имеют общих точек, но у них общий центр

Окружности имеют одну общую точку

Окружности имеют две общие точки

Окружности не имеют общих точек

2.7. Отличие окружности от круга

Окружность представляет собой бесчисленное множество точек, которые находятся на одинаковом расстоянии от одной единственной, называемой центром окружности. Соединенные между собой точки формируют кривую линию, которая и будет окружностью. Все точки, которые находятся на другом расстоянии от центра окружности, не будут находиться на этой линии, поэтому не будут входить в окружность. Соответственно, окружность – это геометрическая фигура, которая представляет собой определенную линию, а все, что находится внутри нее либо снаружи, к окружности не относится. По этой причине имеется четкое понятие, что окружность делит всю плоскость на две части – внутреннюю, ограниченную линией окружности, и внешнюю, безграничную, поскольку плоскость в общем понимании не имеет границ.

Круг является геометрической фигурой, граница которой состоит из бесчисленного множества точек, равноудаленных от центра круга. Все внутреннее пространство, а также центр круга принадлежат ему, таким образом, можно говорить о том, что круг представляет собой некую площадь пространства, ограниченную множеством точек. А поскольку эти точки равноудалены от центра, то границей круга будет окружность. Все внешнее пространство кругу не принадлежит, зато он охватывает всю ту часть плоскости, которая очерчена при помощи окружности.

Различия между кругом и окружностью не столь велики, поскольку эти фигуры представляют собой неисчисляемое количество точек плоскости, находящихся от одной центральной точки на одинаковом расстоянии. Но важным отличительным признаком является тот факт, что внутреннее пространство не принадлежит окружности, но обязательно является составной частью круга. Иными словами, круг представляет собой не только окружность, которая является его границей, но также и то бесконечное число точек, находящихся внутри этой окружности.

Можно сделать следующий вывод. Разница между кругом и окружностью заключается в следующем:

1. Окружность является лишь частью круга, его границей, в то время как круг является более обширной и полноценной фигурой;

2. Окружность – это кривая линия, состоящая из бесчисленного множества точек, равноудаленных от центра, а круг представляет собой не только сумму этих точек окружности, но также и все те точки, которые расположены внутри этой самой окружности.

Проведенная выше работа позволила мне сделать следующие выводы:

1. Наибольшее число частей, на которое можно разделить окружность тремя прямыми равно 7.

2. При стороне квадрата равной 4, периметр и площадь будут выражаться одним целым числом.

3. Существует круг, площадь и длина окружности которого выражаются одним числом, радиус которого равен 2.

4. Существует три случая взаимного расположения на плоскости прямой и окружности: прямая и окружность имеют две общие точки; прямая и окружность имеют только одну общую точку; прямая и окружность не имеют общих точек.

5. Существует четыре случая взаимного расположения на плоскости двух окружностей.

Так же выяснила, что разница между кругом и окружностью заключается в следующем:

1. Глейзер Г.И. История математики в школе 7-8 кл.: Пособие для учителей. –М.: Просвещение, 1982. С. 32.

2. Гусев В.А. Геометрия 5-6 классы: Учеб. пособие.- М.: ООО «Русское слово», 2002. С.118-142.

3. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия: Учеб. пособие для учащихся 5-6 классов. – М.: МИРОС, 1995. С. 72—83.

Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Окружность и круг

Средняя оценка: 4.7

Всего получено оценок: 469.

Средняя оценка: 4.7

Всего получено оценок: 469.

Окружность и круг – это две разные фигуры, которые частенько путают в математике 6 класса. Поэтому имеет смысл обсудить эту тему более подробно.

Видео:Окружность и круг. Центр, радиус, диаметр, хорда, дуга, сектор и длина окружности, площадь круга.Скачать

Определения

Круг – это часть пространства, ограниченная окружностью. Окружность – это множество точек, равноудаленных от одной точке, называемой центром окружности.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Различия

Окружность – это линия. Круг – это плоская фигура. Окружность не может иметь площади, тогда как круг ее имеет.

Рис. 1. Круг и окружность.

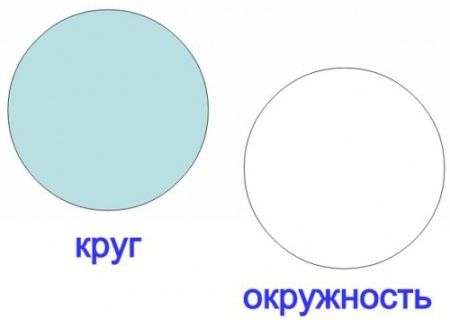
На этом, пожалуй, различия круга и окружности заканчиваются. Но стоит сказать еще и о том, что в геометрии чаще звучит название окружности.

Круг имеет площадь, но в задачах мы чаще ищем длину окружности. На длину окружности завязаны некоторые свойства вписанной и описанной окружности треугольника, поэтому сложилась некая традиция использования окружности вместо круга. Но путать эти фигуры ни в коем случае нельзя.

Видео:Окружность и круг. Длина окружности. Площадь круга. Урок 15. Математика 6 классСкачать

Сходства

Сходства заключаются в характеризующих отрезках. Их несколько для окружности и круга: хорда, радиус и диаметр.

Хорда это отрезок, соединяющий две точки окружности. Хорда может не проходить через центр окружности, а может и проходить.

Если хорда проходит через центр окружности, то она зовется диаметром. Диаметр это отрезок, соединяющий две точки окружности и проходящий через ее центр. Диаметр используется при нахождении площади и длины окружности.

Радиус это любой отрезок, соединяющий центр окружности и точку на окружности. Радиус может использоваться вместо диаметра, так как равен его половине.

Видео:Площадь круга. Практическая часть - решение задачи. 6 класс.Скачать

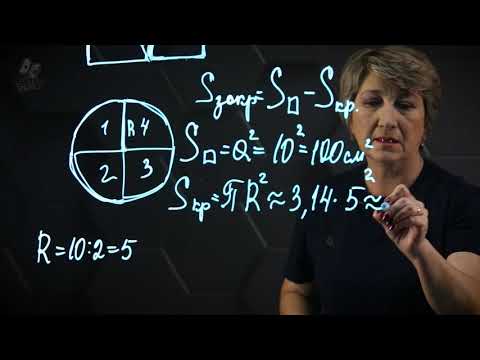
Формулы

Формула площади актуальна только для круга. Окружность не может иметь площади.

$R=<Dover>$-то есть радиус равен половине диаметра. Соответственно это равенство можно подставить в формулу площади и получить еще одну формулу. Или просто найти диаметр или радиус через эту формулу и подставить в уже приведенную формулу.

Существует формула, которая позволяет найти длину окружности. Что такое длина окружности? Если условно распрямить линию окружности, то получится прямая, длину которой можно найти по формуле:

$L=pi*d$ – диаметр, так же, как и в площади можно заменить диаметром.

Рис. 2. Длина окружности.

Видео:5 класс, 22 урок, Окружность и кругСкачать

Окружность и прямая

Положение окружности и прямой на плоскости это отдельная тема для разговора. Прямая на плоскости может:

Пересекать окружность
Не пересекать окружность
Касаться окружности

Прямая, пересекающая окружность зовется секущей и имеет две общие точки с окружностью.

Отдельный интерес имеет касательная прямая, то есть прямая, которая имеет одну общую точку с окружностью. Дело в том, что эта прямая имеет свойство, которое часто помогает в решении задач.

Запомните, радиус, проведенный в точку касания перпендикулярен касательной.

Рис. 3. Окружность и прямая.

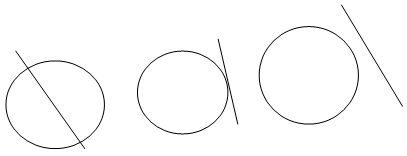
Видео:Математика. 6 класс. Длина окружности. Площадь круга /28.09.2020/Скачать

Окружность и угол

Окружность и угол связаны, потому как окружность это наиболее яркий пример полного угла. То есть, если провести какой либо отрезок и повернуть его вокруг своего начала на 360 градусов, то получится окружность.

Углом в окружности измеряется дуга. Дуга это часть окружности, ограниченная двумя радиусами. Два радиуса и дуга представляют собой сектор.

Видео:Длина окружности. Практическая часть - решение задачи. 6 класс.Скачать

Что мы узнали?

Из статьи мы узнали о том, что круг – это плоская фигура, а окружность – это линия. Мы познакомились с характеристиками этих понятий и узнали свойства круга и окружности.

Видео:МЕРЗЛЯК-6. КРУГ И ОКРУЖНОСТЬ. ПАРАГРАФ-24Скачать

Проект «Окружность и круг»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Развитие управляющих функций мозга ребёнка: полезные советы и упражнения для педагогов

Сертификат и скидка на обучение каждому участнику

МБОУ «Семилуженская СОШ» Томского района

Окружность и круг

Работу выполнил: обучающийся 6 класса

Руководитель: учитель математики

Предметом своего исследования я выбрал окружность и круг , так как ещё в Древней Греции эти фигуры считались венцом совершенства. Действительно, в каждой своей точке окружность «устроена» одинаковым образом, что позволяет ей как бы двигаться по себе.

Формы круга, окружности мы

встречаем повсюду: это и колесо машины

и велосипеда, и линия горизонта, и

монеты, и диск Луны.

Любой дошкольник может

показать из ряда предложенных ему

геометрических фигур кружок. На первый

взгляд, кажется, что круг — очень обычная

и простая фигура, но это далеко не так. На

самом деле окружность и круг таят в себе

множество загадок и тайн, имеют

увлекательную историю их изучения.

Математики стали активно заниматься

изучением этих геометрических фигур

Окружность и круг – это понятия, которые изучаются в школьном курсе математики с начальных классов, но они недостаточно хорошо усваиваются. Поэтому особенно важно изучить свойства этих фигур, особенности, связанные с ними закономерности.

Проблема: Как изменятся длина окружности и площадь круга, если увеличить или

уменьшить радиус? Нужны ли детям рисунки для раскрашивания?

Гипотеза: длина окружности прямо пропорциональна длине радиуса;

площадь круга пропорциональна квадрату длины радиуса;

созданная книжка-раскраска поможет малышам занимать

свое время, учиться применять разноцветные карандаши,

чтобы получать красивые рисунки, которыми можно

радоваться самим и окружающим детям.

Цель работы: исследование зависимости между радиусом, длиной

окружности и площадью круга, создание книжки – раскраски

1. Изучить теоретические сведения о круге и

2. Исследовать изменение длины окружности и площади круга

в зависимости от изменения длины радиуса.

3.Опытным путем вычислить число π.

4. Изучить историю числа.

5. Показать применение материалов исследований при решении

6.Научиться работать циркулем и разработать рисунки.

7.Подарить книжки – раскраски детям из неблагополучных семей.

Изучение теоретического материала

Понятие окружности и круга

Для построения окружностей имеется специальный инструмент — циркуль .

Обратим внимание на то, что при проведении окружности точка А все время находится на одном и том же расстоянии от точки О, называемой центром окружности, а отрезок ОА называется радиусом окружности. Следовательно , окружность – это замкнутая кривая линия, все точки которой находятся на одном и том же расстоянии от ее центра.

Радиус окружности – это отрезок, соединяющий центр окружности с некоторой точкой окружности.

Окружность ограничивает на плоскости определенную часть.

Часть плоскости, которая ограничивается окружностью, называется кругом.

Впервые понятие длины окружности даётся в учебнике математика 6 класса.

«Возьмём круглый стакан, поставим на лист бумаги и обведём его карандашом. На бумаге получится окружность. Если «опоясать» стакан ниткой, а потом распрямить её, то длина нитки будет приближённо равна длине нарисованной окружности». Есть несколько способов непосредственного измерения длины окружности.

1. Вырежьте из картона, фанеры или другого материала круг, поставьте его ребром на лист бумаги, где начерчена прямая линия. Отметьте на прямой и на окружности точку их касания А. Затем плавно катите круг по прямой до тех пор, пока отмеченная точка А на окружности не окажется на прямой в точке В. Отрезок АВ тогда будет равен длине окружности. Измерив его с помощью избранной единицы длины, мы тем самым измерим и длину окружности.

2. Оберните вырезанный из картона (фанеры или другого материала) круг веревочкой по окружности так, чтобы конец веревочки совпал с началом в одной и той же точке окружности. Затем растяните эту веревочку и измерьте ее длину. Длина веревочки будет равна длине окружности.

Однако эти способы непосредственного измерения длины окружности мало удобные и дают они приближенные результаты измерения.

Поэтому уже с древних времен начали искать более совершенные способы измерения длины окружности. В процессе измерений заметили, что между длиной окружности и длиной ее диаметра имеется определенная зависимость.

Чтобы убедиться в этом, я проделал следующий опыт.

С=24,9см

π ≈3,1142857…

Взял несколько кругов, измерил непосредственным способом их окружности и их диаметры, а затем нашёл отношения длины каждой окружности к своему диаметру. Я получил одно и то же значение этого отношения, близкое к числу 3,1.

Многие математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности, и найти более точное значение этого отношения. Впервые это удалось сделать древнегреческому математику Архимеду. Архимед установил, что отношение длины окружности к диаметру есть величина постоянная, и нашел довольно точное значение этого отношения. Это отношение стали обозначать греческой буквой π — первой буквой греческого слова «периферия» — круг (читается «пи»).

Таким образом, для вычисления длины окружности была установлена известная формула C : D = r , отсюда

где С -длина окружности, π = 3,14. D — диаметр окружности.

Так как диаметр окружности вдвое больше её радиуса, то длина окружности с радиусом r равна C = 2π r . Получили другую формулу для длины окружности:

Подсчёты показали, что с точностью до десятитысячных = 3,1415…. Если значение округлить до сотых, то получим значение 3,14.

Площадь круга

На рисунке изображены круг и два квадрата ABCD и EFKM .

Радиус круга равен r , поэтому длина стороны квадрата ABCD равна 2 r , а площадь квадрата 4 r 2 . Площадь треугольника EOF вдвое меньше площади квадрата AEOF , поэтому площадь квадрата EFKM вдвое меньше площади квадрата ABCD , то есть равна 2 r 2 . Площадь круга S больше площади квадрата EFKM , но меньше площади квадрата ABCD : 2 r 2 S _круга r 2

Примерно площадь круга равна 3 r 2 . Можно доказать, что S = πR 2

Можно предложить ещё один интересный и понятный способ вычисления площади круга.

Возьмём круг радиуса R и разрежем его на несколько равных секторов (сектор – это часть круга, ограниченная двумя радиусами и дугой окружности, соединяющей их концы). Для наглядности половину секторов заштрихуем.

А теперь из этих секторов составим другую фигуру. Боковые стороны фигуры можно сделать вертикальными. Для этого нужно разрезать пополам крайний (например, левый) сектор и приставить одну половинку с другой стороны. Площадь новой фигуры такая же, как у круга. А сама фигура похожа на прямоугольник.

Если мы будем разрезать круг на ещё более мелкие секторы, то новая фигура будет ещё более походить на прямоугольник.

Нам известно, что площадь прямоугольника равно произведению его длины на ширину. Ширина прямоугольника — это радиус данной окружности, значит равна R , а длина образована дугами секторов – закрашенных и незакрашенных.

Следовательно, длина равна половине длины окружности, то есть .

Так как C = 2 πR , то = = π R .

Следовательно, площадь прямоугольника равна S = π R ∙ R = π R 2

Но у рассматриваемого первоначально круга площадь была такая же. Вот мы и получили формулу для вычисления площади круга

Зависимость длины окружности от длины её радиуса

Как изменится длина окружности, если её радиус увеличить в 2 раза?

Такой вопрос был задан при социологическом опросе учащимся 5 – 11классов, а также учителям начальных классов и учителям предметов гуманитарного цикла.

Данные, полученные при ответе на этот вопрос, приведены в следующей диаграмме. Всего было опрошено человека: 59 учеников, 16 учителей.

Как видно из диаграммы, большинство опрошенных учащихся и учителей, чья деятельность не связана с математикой, считают, что при увеличении радиуса в 2 раза длина окружности также увеличивается, но только небольшая часть уточняет, что именно в 2 раза.

Чтобы выяснить, так ли это, рассмотрим пример.

Пусть радиус равен 6см, тогда длина окружности равна С = 2π ∙6 = 12 π

Увеличим радиус в 2 раза, то есть он станет 12 см, тогда длина окружности равна С₁ = 2 π ∙12 = 24 π.

Узнаем, во сколько раз увеличилась длина окружности:

Получается, что при увеличении радиуса в 2 раза длина окружности увеличивается также в 2 раза.

После рассмотрения нескольких аналогичных примеров делаем вывод:

при изменении радиуса окружности (увеличении или уменьшении) в k раз её длина изменяется (увеличивается или уменьшается) также в k раз.

Следовательно, длина окружности пропорциональна её радиусу.

Зависимость площади круга от длины его радиуса

При проведении социологического опроса был задан вопрос: «Что произойдёт с площадью круга, если его радиус увеличится в 3 раза?»

Данные, полученные при ответе на этот вопрос, представлены в диаграмме.

Как видно из диаграммы, большинство опрошенных, чья деятельность не связана с математикой, считают, что при увеличении радиуса в 3 раза площадь круга также увеличивается, причём также в 3 раза, и только небольшая часть понимает, что не в 3, а в 9 раз. А вот большинство старшеклассников ответили, что при увеличении радиуса в 3 раза площадь круга увеличивается в 9 раз.

Чтобы выяснить, кто из них прав, рассмотрим пример.

Пусть радиус равен 2см, тогда площадь круга равна S = π ∙ 2 2 = 4π

Чтобы выяснить, кто прав, рассмотрим пример.

Увеличим радиус в 3 раза, то есть он станет 6 см, тогда площадь круга равна S = π ∙ 6 2 = 36 π .

Узнаем, во сколько раз увеличилась площадь круга:

Получается, что при увеличении радиуса круга в 3 раза его площадь увеличивается в 9 раз.

После рассмотрения нескольких аналогичных примеров получаем вывод:

при изменении радиуса круга в k раз его площадь изменяется также в k ² раз.

Изменение радиуса окружности при изменении её длины

Пусть первоначальный радиус окружности равен R ₁метров, тогда первоначальная длина окружности равна

Увеличим длину окружности на a метров, то есть она станет C ₂ = C ₁ + a (метров), тогда увеличится и радиус окружности, он станет равен

(метров)

Найдём увеличение радиуса:

Интересно, что в окончательный ответ не входит величина первоначального радиуса. Поэтому результат получится одинаковый для любой окружности. Вообще, разность длин двух концентрических окружностей не зависит от их радиусов, а только от расстояния между ними. Прибавка одного сантиметра к радиусу земной орбиты увеличила бы её длину настолько, насколько удлинится от такой же прибавки радиуса окружность, например, пятака. На этом геометрическом парадоксе (парадокс – истина, кажущаяся неправдоподобной) основано много любопытных задач.

Задача №1 «По экватору»

Вообразите, что Вы обошли Земной шар по экватору. На сколько при этом верхушка Вашей головы прошла более длинный путь, чем кончик Вашей ноги, если Ваш рост 1,7м?

Решение. Пусть R – радиус Земного шара, тогда ноги прошли путь . Верхушка же головы при этом прошла путь 2π( R + 1,7). Разность пройденных расстояний равна 2π( R + 1,7) — 2π R = 2π R + 3,4π — 2π R = 3,4π ≈ 3,4 ∙ 3,14 = 10,676 ≈10,7, то есть рост человека , умноженный на 2 π .

Задача №2 «Земной шар и мышь»

Если обтянуть земной шар по экватору проволокой и затем прибавить к её длине 1м, то сможет ли между проволокой и землёй проскочить мышь?

Обычно отвечают, что промежуток будет тоньше волоса: что значит прибавка в один метр по сравнению с 40 миллионами метров земного экватора. В действительности же величина промежутка равна (100 : 2π)см ≈ 16см. Не только мышь, но и крупный кот проскочит в такой промежуток.

пи – первая буква греческого слова «периферия», что в переводе означает окружность. Первым ввёл обозначение отношения длины окружности к диаметру современным символом английский математик

У. Джонсон в 1706 г.

В клинописных табличках Древнего Междуречья содержится запись о том, что длина окружности в 3 раза больше диаметра.

Однако уже во 2 тысячелетии до н.э. математики Древнего Египта находили более точное отношение. По точным расчётам Архимеда отношение окружности к диаметру заключено между числами 3 и 3, а это означает, что  =3,1419… Архимед указал границы числа 3,1408  В 1596 году голландский математик Ван Цейлен нашел 32 первых знака числа «пи», в 1719 году французский математик Ланьи вычисляет «пи» со 140 верными знаками. В 1844 году немец Дазе нашел «пи» с 200 знаками, в конце XIX века было уже известно более 500 верных знаков числа «пи».

Математик 16 века Лудольф, в Лейдене, имел терпение вычислить число «пи» с 35 десятичными знаками и завещал вырезать это значение для π на своём могильном памятнике.

Английский математик Август де Морган назвал как-то p «…загадочным числом 3,14159…, которое лезет в дверь, в окно и через крышу».

А так выглядит 101 знак числа “ пи” без округления:

3, 14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679.

В наше время с помощью ЭВМ число  вычислено с миллионами правильных знаков после запятой. Но такая точность не нужна ни в каких вычислениях и представляет скорее технический, чем научный интерес.

Число π присутствует в чертежах и вычислениях, выполняемых электронными машинами при подготовке и проведении полетов в космос; оно представляет необходимое количество своих десятичных знаков всякий раз, когда они нужны инженерам, рассчитывающим цилиндрические, сферические или конические части машин, физикам и астрономам, когда они проводят приближенные вычисления по формулам, в которых среди фундаментальных постоянных появляется и π . Куда бы мы ни обратили свой взор, мы видим проворное и трудолюбивое число π: оно заключено и в самом простом колесике, и в самой сложной автоматической машине.