Докажите что у прямой призмы основания равны и параллельны

Решебник по геометрии за 11 класс (А.В. Погорелов, 2001 год),
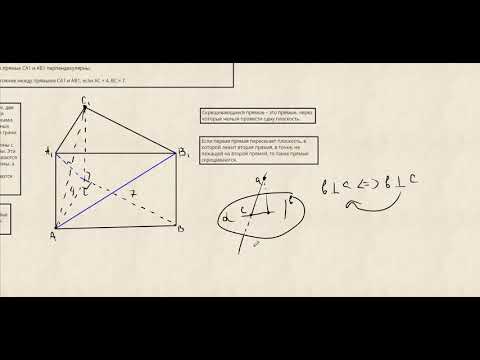
задача №5
к главе «§ 20. Многогранники».

Выделите её мышкой и нажмите CTRL + ENTER

Большое спасибо всем, кто помогает делать сайт лучше! =)

Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок № 14. Призма

Перечень вопросов, рассматриваемых в теме:

• Понятие призмы и виды призм;
• Элементы призмы: вершины, ребра, грани;
• Понятие площади боковой поверхности и площади полной поверхности призмы, формулы для вычисления;
• Призма как модель реальных объектов;
• Пространственная теорема Пифагора.

Глоссарий по теме

Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

Боковые грани – все грани, кроме оснований.

Боковые ребра – общие стороны боковых граней.

Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.

Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.

Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.

Площадь полной поверхности призмы – сумма площадей всех ее граней.

Площадь боковой поверхности призмы – сумма площадей ее боковых граней.

Параллелепипед – призма, все грани которой – параллелограммы.

Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,

геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.

Открытые электронные ресурсы:

Открытый банк заданий ФИПИ http://ege.fipi.ru/

Теоретический материал для самостоятельного изучения

Определение призмы. Элементы призмы.

Рассмотрим два равных многоугольника А₁А₂. А_n и В₁В₂. В_n, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А₁В₁, А₂В₂. А_nВ_n, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).

Рисунок 1 – Призма

Заметим, что каждый из n четырехугольников (A₁A₂B₁B_2, . A_nA₁B₁B_n) является параллелограммом. Убедимся в этом на примере четырехугольника A₁A₂B₁B₂. A₁A₂ и B₁B₂ параллельны по свойству параллельных плоскостей, пересеченных третьей плоскостью. А₁В₁ и А₂В₂ по условию. Таким образом, в четырехугольнике A₁A₂B₁B₂ противоположные стороны попарно параллельны, значит этот четырехугольник — параллелограмм по определению.

Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.

При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.

Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).

Рисунок 2 – Наклонная призма

Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.

Высота прямой призмы равна ее боковому ребру.

На рисунке 3 приведены примеры прямых призм

Рисунок 3 – Виды призм.

Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.

Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.

Площадь полной поверхности призмы. Площадь боковой поверхности призмы.

Площадью полной поверхности призмы (S_полн) называется сумма площадей всех ее граней, а площадью боковой поверхности (S_бок) призмы – сумма площадей ее боковых граней.

Таким образом, верно следующее равенство: S_полн= S_бок+2S_осн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.

Чему равна площадь боковой поверхности прямой призмы?

Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом S_бок=P_оснh.

Пространственная теорема Пифагора

Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.

Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.

Рисунок 4 – Прямоугольный параллелепипед

Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁ и найдем квадрат длины его диагонали А₁С.

Для этого рассмотрим треугольник А₁АС:

Ребро АА₁ перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА₁ перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА₁АС – прямоугольный.

По теореме Пифагора получаем: А₁С 2 =АА₁ 2 +АС 2 (1).

Выразим теперь АС. По условию в основании лежит прямоугольник, значит ΔАВС – прямоугольный. По тереме Пифагора получаем: АС 2 =ВС 2 +АВ 2 .

Подставив результат в (1), получим: А₁С 2 =АА₁ 2 +ВС 2 +АВ 2 .

Так как в основании прямоугольник, то ВС=АD.

Таким образом, А₁С 2 =АА₁ 2 +АD 2 +АВ 2 .

Что и требовалось доказать

Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.

Примеры и разбор решения заданий тренировочного модуля

Найдите для каждой картинки пару

1)2) 3)

4)5)

6)

Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.

Какие из перечисленных объектов могут быть элементами призмы?

1) параллельные плоскости

Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.

Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.

Видео:№218. Докажите, что: а) у прямой призмы все боковые грани — прямоугольники; б) у правильнойСкачать

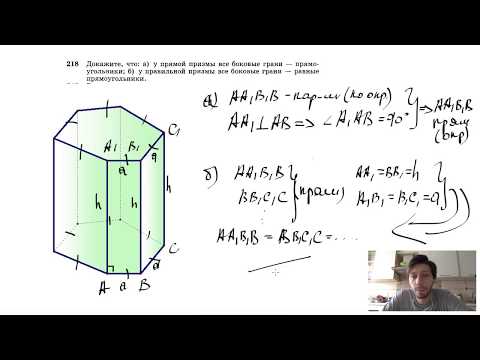
Стереометрия. Страница 5

Видео:№282. Прямые а и b параллельны. Докажите, что середины всех отрезков XY, где Х∈а, Y∈bСкачать

1. Двугранный, трехгранный углы

Двугранный угол представляет собой фигуру, образованную двумя полуплоскостями и общей ограничивающей их прямой. Полуплоскости называются гранями двугранного угла, а прямая, ограничивающая их, — ребром (Рис.1).

Если провести плоскость, перпендикулярную ребру двугранного угла, то она пересечет его грани по двум полупрямым. Угол, образованный между двумя этими полупрямыми, называется линейным углом двугранного угла.

Градусная мера двугранного угла равна градусной мере линейного угла. Величина двугранного угла не зависит от выбора линейного угла, т.е. плоскости, перпендикулярной ребру двугранного угла.

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

7. Правильные многогранники

Если выпуклый многогранник имеет все грани правильные многоугольники с равным числом сторон и в каждой вершине многоугольника сходится одно и то же число ребер, то такой многогранник называется правильным.

Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

Тетраэдр это многогранник, у которого грани правильные треугольники.

Куб это многогранник, у которого все грани — квадраты.

Октаэдр — многогранник, который представляет собой две пирамиды с общим основанием. Основание этих пирамид — квадрат.

Додекаэдр это многогранник, у которого грани правильные пятиугольники. В каждой вершине сходится по три ребра.

Икосаэдр это многогранник, у которого грани правильные треугольники. В каждой вершине сходится по пять ребер.

8. Пример 1

Докажите, что сечение призмы, параллельное основаниям, равно основаниям.

Доказательство:

Пусть дана призма АВСA’B’C’ (Рис.7). Основания призмы равны и являются треугольниками. Они лежат в параллельных плоскостях и совмещаются параллельным переносом. Отсюда следует, что боковые ребра параллельны и равны.

Если провести плоскость α, параллельную основаниям, то в сечении получится такое же основание. Так как сторона A»C» параллельна АС, A»B» — AB, B»C» — BC. А так как боковые ребра AA’, BB’, CC’ параллельны, то АА»C»C, AA»B»B, BB»C»C прямоугольники (параллелограммы, если АВСA’B’C’ наклонная призма).

Отсюда следует, что A»C» = AC, A»B» = AB, B»C» = BC. Таким образом, треугольник A»B»C» равен треугольнику АВС и A’B’C’ соответственно. Отсюда можно сделать и общий вывод: если в основании призмы будет лежать како-либо многоугольник, то в сечении, параллельном основаниям, получится такой же многоугольник.

Рис.7 Задача. Докажите, что сечение призмы.

Пример 2

Боковое ребро наклонной призмы равно 16 м. Оно наклонено к плоскости основания под углом 30°. Найдите высоту призмы.

Решение:

Пусть дана наклонная призма АВСA’B’C’ (Рис. 8). Рассмотрим нижнее основание — треугольник АВС. Проведем прямую а через точку А в плоскости основания, перпендикулярную A’A. Проведем также прямую АР, перпендикулярную прямой а. Таким образом, прямая АР является проекцией наклонной A’A на плоскость основания. А плоскость, в которой лежит треугольник AA’P, перпендикулярна плоскости основания.

Рассмотрим треугольник AA’P. Угол A’AP равен 30° по условию задачи. Опустим высоту A’O. В прямоугольном треугольнике AA’O найдем A’O.

sin 30° = A’O / AA’ . Отсюда:

A’O = AA’ sin 30° = 16 / 2 = 8 м.

Рис.8 Задача. Боковое ребро наклонной призмы равно 15 м.

Пример 3

В правильной четырехугольной призме через середины двух смежных сторон основания проведена плоскость, пересекающая три боковые ребра и наклоненная к плоскости основания под углом 60°. Сторона основания равна 8 м. Найдите площадь полученного сечения.

Решение:

Пусть дана правильна четырехугольная призма АВСDA’B’C’D’ (Рис. 9). Заметим, что многоугольник PBCDF является проекцией многоугольника PKHSF на плоскость основания, площадь которого необходимо найти. Следовательно, найдем площадь многоугольника PBCDF.

S_PBCDF = 8 2 — (8/2) 2 /2 = 56 м 2

Теперь найдем площадь многоугольника PKHSF из формулы:

S_PKHSF = S_PBCDF / cos 60° = 56 / 1 / 2 = 112 м 2

Рис.9 Задача. В правильной четырехугольной призме.

Пример 4

Боковая поверхность правильной четырехугольной призмы 12 м 2 . А полная поверхность 20 м 2 . Найдите высоту призмы.

Решение:

Пусть дана правильная четырехугольная призма АВСDA’B’C’D’ (Рис. 10). Так как призма имеет четыре боковые грани, то площадь одной боковой грани составляет 1/4 часть боковой поверхности.

S_AA’D’D = S_бок / 4 = 12 / 4 = 3 м 2

Площадь основания призмы равна половине разности площадей между полной поверхностью призмы и ее боковой поверхностью.

2 S_ABCD = S_пол — S_бок = 20 — 12 = 8 м 2

Так как площадь боковой грани составляет 3 м 2 , то высоту призмы, т.е. AA’, можно найти из формулы:

Следовательно, высота призмы составляет 3 / 2 м.

Рис.10 Задача. Боковая поверхность правильной четырехугольной призмы.

Пример 5

Основание пирамиды — ромб с диагоналями 6 м и 8 м. Высота пирамиды проходит через точку пересечения диагоналей ромба и равна 7 м. Найдите боковую поверхность пирамиды.

Решение:

Пусть дана пирамида АВСDS (Рис. 11). Основание пирамиды — ромб ABCD с диагоналями АС = 8 м, BD = 6 м. Высота SO = 7 м.

По теореме Пифагора найдем боковые ребра SA и SD:

SA 2 = AO 2 + SO 2 = 4 2 + 7 2 = 65

SD 2 = OD 2 + SO 2 = 3 2 + 7 2 = 58

SA = , SD =

Теперь найдем сторону ромба AD:

AD 2 = AO 2 + OD 2 = 3 2 + 4 2 = 25 , AD = 5 м

Теперь по теореме косинусов найдем косинус угла α между боковыми ребрами:

AD 2 = SA 2 + SD 2 — 2 SA SD cos α = 65 + 58 — 2 cos α = 25

Отсюда, cos α = 49 / , sin α = 1369 /

Теперь найдем площадь боковой грани S_ASD:

S_ASD = SA SD sin α / 2 = 1369 / / 2 = 18.5 м 2

Отсюда, S_бок = 4 S_ASD = 4 * 18.5 = 74 м 2

📹 Видео

№99. Докажите, что три параллельные плоскости отсекают на любых двух пересекающих эти плоскостиСкачать

10 класс, 13 урок, ПараллелепипедСкачать

Геометрия 11 класс (Урок№13 - Вычисление объемов с помощью определенного интеграла.)Скачать

Задача 14 (С2) из проф ЕГЭ 2017 по математикеСкачать

ЕГЭ стереометрия Сечение призмы Площадь сеченияСкачать

Главная > Учебные материалы > Математика: Стереометрия. Страница 5 1.Двугранный, трехгранный углы. 2.Призма и построение ее сечений. 3.Параллелепипед. 4.Прямоугольный параллелепипед. 5.Пирамида. 6.Усеченная пирамида. 7.Правильные многогранники. 8.Примеры.
1 2 3 4 5 6 7 8
Рис. 1 Двугранный угол. Видео:Геометрия 11 класс (Урок№12 - Объемы прямой призмы и цилиндра.)Скачать Трехгранный углы Пусть заданы три луча a, b, c не лежащие в одной плоскости и исходящие из одной общей точки О. (Рис.1.1). Тогда трехгранным углом называется фигура, которая состоит из трех плоских углов. Точка О, из которой исходят лучи, называется вершиной трехгранного угла. Сами углы называются гранями, а стороны — ребрами. Понятие многогранного угла можно определить аналогичным образом.	Рис. 1.1 Трехгранный угол. Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать 2.Призма и построение ее сечений Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать Прямая призма Призмой называется многогранник, у которого две стороны являются плоскими многоугольниками, лежащими в параллельных плоскостях и совмещаемых параллельным переносом, а боковые грани состоят из всех отрезков, соединяющих соответствующие точки этих многоугольников (Рис.2). Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие точки оснований, ее ребрами. Высотой призмы называется расстояние между ее основаниями. Если боковые ребра призмы перпендикулярны основанию, то такая призма называется прямой. В противном случае призма называется наклонной. Боковые ребра у призмы параллельны и равны. Боковые грани прямой призмы являются прямоугольниками. Если в основании призмы лежит правильный многоугольник, то такая призма называется правильной. Теорема: площадь боковой поверхности прямой призмы равна произведению периметра основания призмы на ее высоту. В основании призмы лежит правильный многоугольник. Боковые ребра призмы находятся под прямым углом к основанию и являются высотами. Боковые грани представляют собой прямоугольники. Отсюда следует, что площадь боковой поверхности призмы равна: где a1, a2, a3, . an — длины сторон основания l — высота призмы p — периметр основания Полная площадь призмы равна сумме площадей двух оснований и боковой поверхности. Рис.2 Прямая призма Видео:Объем прямой призмы | Геометрия 11 класс #23 | ИнфоурокСкачать Наклонная призма Если боковые ребра призмы находятся под некоторым углом к основанию, то призма является наклонной (Рис.2.1). Используя правила параллельного проектирования, изображение призмы можно построить следующим образом. Сначала строится одно из оснований, т.е. многоугольник, а затем проводят боковые ребра из каждой вершины основания, которые параллельны и равны между собой. Затем концы этих отрезков соединяются и строится другое основание призмы. Для того, чтобы построить сечение призмы плоскостью, сначала задают прямую g в плоскости одного из оснований, которая называется следом. Затем проводят через заданную точку В прямую, которая находится в плоскости грани, и соединяют ее с заданным следом в точке Е. Отрезок АС на рассматриваемой грани есть пересечение этой грани с секущей плоскостью. Если грань, которая содержит точку В, параллельна следу, то секущая плоскость пересекает эту грань по отрезку, параллельному заданному следу и проходящему через точку В. Таким образом, можно провести отрезки на всех гранях призмы и получить сечение плоскостью с заданным следом. Рис.2.1 Наклонная призма Видео:Параллельность прямой и плоскости. 10 класс.Скачать 3. Параллелепипед Призма, у которой основание есть параллелограмм, называется параллелепипедом. Параллелепипед, у которого грани расположены под некоторым углом ≠ 90° к основанию, называется наклонным. В противном случае — прямым, т.е. угол между боковыми гранями и основанием = 90°. Теорема. Противолежащие грани параллелепипеда параллельны и равны. Доказательство. Пусть дан параллелепипед ABCDA’B’C’D’ (Рис.3). Рассмотрим грани параллелепипеда AA’D’D и BB’C’C. Так как основания параллелепипеда параллелограммы, то сторона AD параллельна и равна стороне ВС, а сторона A’D’ параллельна и равна стороне B’C’. Сторона AB параллельна и равна стороне DС, а сторона A’B’ параллельна и равна стороне D’C’. Отсюда можно сделать вывод, что грани AA’D’D и BB’C’C лежат в параллельных плоскостях. Таким образом, грань AA’D’D совмещается параллельным переносом с гранью BB’C’C. Следовательно эти грани равны. Аналогично можно доказать параллельность и равенство граней DD’C’C и AA’B’B. Видео:№298. На рисунке 145 AD||BE, AC=AD и ВС=ВЕ. Докажите, что угол DCE — прямой.Скачать Центральная симметрия параллелепипеда Теорема. Диагонали параллелепипеда пересекаются в одной точке, которая делит их пополам. Рассмотрим две грани параллелепипеда ABCD и BB’C’C. Сторона BC у них общая. Следовательно стороны AD и B’C’ равны, лежат на параллельных прямых и в одной плоскости. Так как грани параллелепипеда AA’B’B и DD’C’C лежат в параллельных плоскостях и совмещаются параллельным переносом, то диагонали AB’ и DC’ параллельны и лежат в плоскости сторон AD и B’C’. Отсюда можно сделать вывод, что AB’C’D — параллелограмм. Диагонали этого параллелограмма пересекаются в точке, которая делит их пополам. Отсюда следует, что точка пересечения диагоналей параллелепипеда является его центром симметрии. Рис. 3 Наклонный параллелепипед. Видео:№521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположныеСкачать 4.Прямоугольный параллелепипед Прямой параллелепипед, у которого основание является прямоугольником, называется прямоугольным. Длины не параллельных ребер параллелепипеда называются его линейными размерами. Теорема. В прямоугольном параллелепипеде квадрат диагонали равен сумме квадратов трех его измерений. Доказательство. Пусть дан параллелепипед ABCDA’B’C’D’ (Рис.4). Рассмотрим прямоугольный треугольник ACC’. Cторонами данного треугольника являются диагональ параллелепипеда AC’, диагональ основания AC и ребро боковой грани CC’. Тогда по теореме Пифагора находим: Рис. 4 Прямоугольный параллелепипед. AC’ 2 = AC 2 + CC’ 2 AC 2 = AD 2 + DC 2 Следовательно: AC’ 2 = AD 2 + DC 2 + CC’ 2 Стороны AD, DC, CC’ являются линейными размерами параллелепипеда. Видео:10 класс, 30 урок, ПризмаСкачать Симметрия прямоугольного параллелепипеда Прямоугольный параллелепипед имеет центр симметрии. Если все три измерения параллелепипеда разные, то он имеет три плоскости симметрии, которые проходят через центры граний (Рис.4.1) Если параллелепипед имеет два равных измерения, то у него есть еще две плоскости симметрии, которые проходят через диагональные сечения. Если у параллелепипеда все три линейные размера равны, то он является кубом. И у него девять плоскостей симметрии. Рис. 4.1 Симметрия прямоугольного параллелепипеда. 5. Пирамида Пирамидой называется многогранник, который состоит из многоугольника в основании, точки, не лежащей в плоскости основания, и всех отрезков, соединяющих вершины многоугольника и данную точку (Рис.5). Точка, не лежащая в плоскости основания, называется вершиной пирамиды. Отрезки, соединяющие вершины основания с вершиной пирамиды, называются боковыми ребрами. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания, называется высотой пирамиды. На рисунке 5 изображена пирамида, в основании которой лежит правильный шестиугольник. A1A2A3A4A5A6 Видео:№388. Докажите, что в равнобедренной трапеции: а) углы при каждом основании равныСкачать Построение пирамиды и ее плоских сечений Для того чтобы построить пирамиду, необходимо сначала построить основание — плоский многоугольник. Затем взять точку, не лежащую в плоскости основания, и соединить ее боковыми ребрами с вершинами основания. Сечения пирамиды, проходящие через ее вершину, представляют собой треугольники. Например, треугольниками являются диагональные сечения, т.е. сечения, проходящие через два несоседних боковых ребра . Сечение пирамиды с боковым следом строится аналогично, как и сечение призмы (Рис.5). Т.е. сначала задается прямая в плоскости основания — след g. Затем берется какая-нибудь точка В, принадлежащая сечению, и строится пересечение следа g секущей плоскости c плоскостью этой грани — точка D. Полученный таким образом отрезок АС, представляет собой линию пересечения плоскости грани и плоскости сечения пирамиды. Если точка В лежит на грани, параллельной следу g (Рис.5.1), то секущая плоскость пересекает эту грань по отрезку BC, параллельному следу g. Концы отрезка также соединяют со следом по прямой ED в плоскости α другой грани и получают прямую пересечения этой грани с плоскостью сечения и т.д. Таким образом можно построить линии пересечения плоскости сечения со всеми гранями пирамиды. Рис. 5.1 Построение пирамиды и ее плоских сечений. Видео:Геометрия 11 класс: Объем призмы и цилиндра. ВидеоурокСкачать 6. Усеченная пирамида Теорема. Плоскость, пересекающая пирамиду и параллельная ее основанию, отсекает подобную пирамиду. Пусть дана пирамида ABCDES. ABCDE — основание пирамиды, пятиугольник. S — вершина пирамиды. α — секущая плоскость. Подвергнем пирамиду преобразованию подобия (гомотетии) с коэффициентом подобия k относительно вершины S. Так как при преобразовании подобия расстояние от вершины до точек фигуры изменяется в одно и тоже k число раз, то пятиугольник в основании переходит в плоскость α, параллельную основанию, т.е. секущую плоскость. Точки A’B’C’D’E’ — точки пересечения боковых ребер пирамиды с плоскостью α. И пирамида, которая образуется путем отсечения данной пирамиды плоскостью α, является подобной данной. Видео:11 класс, 31 урок, Объем прямой призмыСкачать Правильная пирамида Если основание пирамиды есть правильный многоугольник, а основание высоты совпадает с центром этого многоугольника, то такая пирамида называется правильной. Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой. Теорема. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему. Рис. 6 Усеченная пирамида.
Рис. 6 Правильные многогранники.