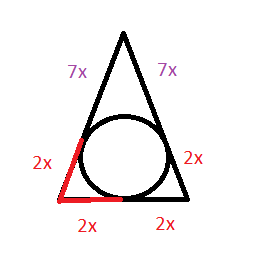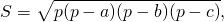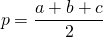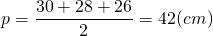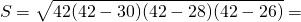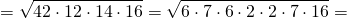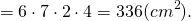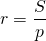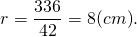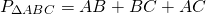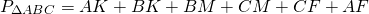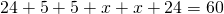Делится точкой касания вписанной окружности в отношении

Условие

боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 2 делить на 7 считая от вершины угла при основании треугольника найдите стороны треугольника если его периметр равен 110 см

Решение

Пусть в одной части х см.
Отношение 2:7 можно записать как 2х:7х.

По свойству касательной к окружности, проведенной из одной точки, отрезки касательных равны ( см. рисунок).

Поэтому боковые стороны имеют длину 2х+7х=9х
основание 2х+2х=4х
9х+9х+4х=110
22х=110
х=5
9*5=45 см -боковая сторона
4*5=20 см — основание

Почему основание ,2х+2х

По свойству касательной к окружности, проведенной из одной точки, отрезки касательных равны

Почему равняется 9х

7x черного цвета и 2х красного, всего 9х, треугольник равнобедренный. Одна боковая сторона 9х и вторая 9х, основание 2х+2х=4х

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 7 : 5, считая от вершины треугольника?

Математика | 5 — 9 классы

Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 7 : 5, считая от вершины треугольника.

Найдите стороны треугольника, если его периметр равен 68 см.

Центрвписанной окружности находится на пересечении биссектрис углов.

По свойству биссектрис основание равнобедренного треугольника делится на 2 части по 5 единиц (как нижняя часть боковой стороны).

Тогда периметртреугольника состоит из 2 * 12 + 10 = 34 части.

Одна часть равна 68 / 34 = 2 см.

Отсюда определяем сторонытреугольника : — боковые 2 * 12 = 24 см, — основание 2 * 10 = 20 см.

Пусть дан равнобедренный тр — к АВС с основаниемАС ; опустим высоту ВЕ на него, проведем биссектрису угла А до пересечения с ВЕ в т.

О ; (центр вписанной окружности лежит в т.

Пересечения биссектрис тр — ка) ; из т.

О опустим перпендикуляр на АВ, он пересечет АВ в т.

Д ; ОД = ОЕ = R(вписанной окружности).

Тр — ки АДО и АОЕ ; они равны по общей гипотенузе и острому углу(АО — биссектриса) или по гипотенузе и катетам — радиусам ОД и ОЕ ; отсюда АД = АЕ.

По условию ВД : ДА = 7 : 5 ; пусть ВД = 7х ; АД = 5х ; тогда АЕ = 5х ; ЕС = 5х( высота ВЕ является и медианой) ; ВС = АВ = 12х.

Периметр = 12х + 12х + 5х + 5х = 68 см ; 34х = 68 ; х = 2 см ;

Ответ : 24см ; 24 см ; 20см.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

В равнобедренный треугольник abc с основанием ac и периметром 13 вписана окружность, k — точка касания этой окружности со стороной bc?

В равнобедренный треугольник abc с основанием ac и периметром 13 вписана окружность, k — точка касания этой окружности со стороной bc.

Найдите основание ac, если bk = 6.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Боковая сторона равнобедренного треугольника на 10см больше основания?

Боковая сторона равнобедренного треугольника на 10см больше основания.

Периметр треугольника равен 26см.

Найдите длины сторон треугольника.

Видео:ЕГЭ Математика Задание 6#27935Скачать

В равнобедренный треугольник вписан ромб так что одна его сторона лежит на основании, а другая на боковой стороне треугольника?

В равнобедренный треугольник вписан ромб так что одна его сторона лежит на основании, а другая на боковой стороне треугольника.

Сторона ромба равна 10 см а периметр треугольника равен 75.

Найдите стороны треугольника.

Видео:Геометрия В равнобокую трапеция вписана окружность Одна из ее боковых сторон точкой касания делитсяСкачать

В равнобедренный треугольник с боковой стороной 15 см и периметром 54 см вписана окружность?

В равнобедренный треугольник с боковой стороной 15 см и периметром 54 см вписана окружность.

Найдите радиус этой окружности.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Точка касания вписанной в равнобедренный треугольник окружности делит боковую сторону на отрезки длины 3 и 2, считая от вершины?

Точка касания вписанной в равнобедренный треугольник окружности делит боковую сторону на отрезки длины 3 и 2, считая от вершины.

Найдите площадь треугольника.

Видео:100 тренировочных задач #74Скачать

Боковая сторона равнобедреного треугольника на 13 см больше его основания?

Боковая сторона равнобедреного треугольника на 13 см больше его основания.

Периметр треугольника равен 68 см.

Найдите стороны треугольника.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Основпние равнобедренного треугольника на 7 см больше его боковой стороны?

Основпние равнобедренного треугольника на 7 см больше его боковой стороны.

Найдите боковую сторону треугольника, если его периметр равен 43 см.

Видео:ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА по геометрии 7 классСкачать

Я туплю?

Найдите основание равнобед.

Треугольника, если центр вписанной в него окружности делит высоту, проведенную к основанию, в отношении 12 : 5, считая от вершины, а боковая сторона равна 60.

Видео:SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

В равнобедренном треугольнике высота проведенная к боковой стороне делит ее на отрезки 4 см и 1 см считая от вершины угла между боковыми сторонами?

В равнобедренном треугольнике высота проведенная к боковой стороне делит ее на отрезки 4 см и 1 см считая от вершины угла между боковыми сторонами.

Найдите основание равнобедренного треугольника.

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

В равнобедренном треугольнике высота, опущенная на боковую сторону, делит ее на отрезке, равные 7 и 2, считая от вершины?

В равнобедренном треугольнике высота, опущенная на боковую сторону, делит ее на отрезке, равные 7 и 2, считая от вершины.

Найдите основание треугольника.

На этой странице находится ответ на вопрос Боковая сторона равнобедренного треугольника делится точкой касания вписанной окружности в отношении 7 : 5, считая от вершины треугольника?, из категории Математика, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Математика. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

1)2(x — 1) — 5 = 5x + 2 2x — 5x = 2 + 2 + 5 — 3x = 9 x = 3 2)4(3x + 5) — 14 = 2(x — 7) 12x — 2x = — 20 10x = — 20 x = — 2.

7m + 42 — 12 + 4m = 19 7m + 4m = 19 + 12 — 42 11m = — 11 M = — 1.

7(m + 6) — 4(3 — m) = 19 7m + 42 — 12 + 4m = 19 11m + 30 = 19 11m = 19 — 30 11m = — 11 m = — 1.

56 : 7 = в 8 раз больше примеров.

320 + 280 + 230 + 90 + 80 = 1000 овец всего 1 сектор — Алексеевская(80 овец) 2 сектор — Васильево (230 овец) 3 сектор — Ивановская (280 овец) 4 сектор — Петровская (320 овец) 5 сектор — Семеновская (90 овец) 1000 — 100% 230 — х х = 230 * 100 / 1000 =..

Простой текст чтобы пустили написать два варианта на второй вопрос а) 86% б) 7.

А = 2 * 2 * 2 * 2 * 2 * 5 * 11 = 1760 b = 2 * 2 * 2 * 5 * 5 * 5 * 11 * 11 = 121000 НОД (a ; b) = 2 * 2 * 2 * 5 * 11 = 440 — наибольший общий делитель 1760 : 440 = 4 121000 : 440 = 275 НОК (a ; b) = 2 * 2 * 2 * 2 * 2 * 5 * 5 * 5 * 11 * 11 = 484000 — н..

38 : 0, 5 вот твой ответик.

Только второе не решено.

8. 75 = 10. 5 : x 8. 75 = 105 / 10 : x 8. 75 = 105 / 10x 8. 75 = 21 / 2x, x = o 17. 5x = 21 X = 21 : 17. 5 X = 1. 2.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Узнать ещё

Знание — сила. Познавательная информация

Видео:Задание 16 ЕГЭ по математике #6Скачать

Вписанная в треугольник окружность делит сторону на отрезки

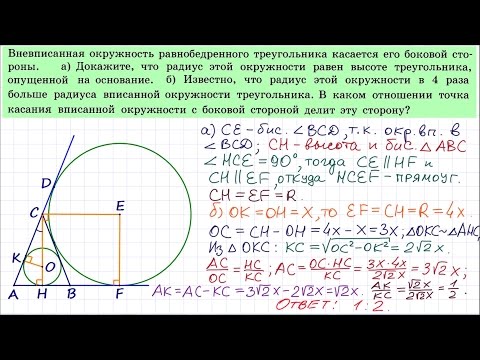
Если в задаче вписанная в треугольник окружность делит его сторону на отрезки, один из возможных вариантов решения — использование свойства отрезков касательных к окружности, проведенных из одной точки.

Рассмотрим две задачи на вписанную в треугольник окружность, решение которых опирается на это свойство касательных.

Одна из сторон треугольника равна 30 см, а другая делится точкой касания вписанной окружности на отрезки длиной 12 см и 14 см, считая от конца неизвестной стороны. Найти радиус вписанной окружности.

Дано: ∆ ABC,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AB, BC, AC,

AB=30 см, CM=12 см, BM=14 см.

1) По свойству касательных, отрезки касательных, проведенных из одной точки, равны:

CF=CM=12 см, BK=BM=14 см, AF=AK=AB-BK=30-14=16 см.

AC=AF+CF=16+12=28 см, BC=BM+CM=14+12=26 см.

2) По формуле Герона,

где a, b, c — стороны треугольника, p — полупериметр,

3) Радиус вписанной окружности найдем по формуле

В треугольнике, периметр которого равен 60 см, одна из сторон делится точкой касания вписанной в него окружности на отрезки 24 см и 5 см. Найти площадь треугольника.

Дано: ∆ ABC,

окружность (O, r) — вписанная,

K, M, F — точки касания со сторонами AB, BC, AC,

1) По свойству касательных, проведенных из одной точки, AF=AK=24 см, BM=BK=5 см, CF=CM= x см.

Следовательно, CM=CF=1 см, AB=AK+BK=29 см, BC=BM+CM=6 см, AC=AF+CF=25 см.

2) Полупериметр равен половине периметра: p=60:2=30 см.

🎦 Видео

Задание 25. Тест 17. ОГЭ. Математика.Скачать

Решение задания 16 математика ЕГЭ 2017Скачать

✓ Как вневписанная окружность Герону помогла | Ботай со мной #083 | Борис ТрушинСкачать

ВСЕ О СЕЧЕНИЯХ В СТЕРЕОМЕТРИИСкачать

Задача по геометрии.Скачать

6.31.1. Планиметрия. Гордин Р.К.Скачать

Пара фактов про окружность | Ботай со мной #067 | Борис Трушин |Скачать