Вписанный угол окружности — это угол, образованный двумя хордами, исходящими из одной точки, то есть вписанным углом называется угол, вершина которого лежит на окружности.
Угол ABC — вписанный угол. ∠ABC опирается на дугу AC, заключённую между его сторонами.
- Теорема о вписанном угле
- Следствия из теоремы
- Теорема с доказательством Вписанный угол измеряется половиной дуги, на которую он опирается.
- Углы, связанные с окружностью
- Вписанные и центральные углы
- Теоремы о вписанных и центральных углах
- Теоремы об углах, образованных хордами, касательными и секущими
- Доказательства теорем об углах, связанных с окружностью
- 🔍 Видео
Видео:8 класс, 34 урок, Теорема о вписанном углеСкачать

Теорема о вписанном угле
Теорема:
Вписанный угол измеряется половиной дуги, на которую он опирается.
Это следует понимать так: вписанный угол содержит в два раза меньше градусов, чем дуга, на которую он опирается:
| ∠ABC = | 1 |  AC. AC. |
| 2 |
При доказательстве этой теоремы следует рассмотреть три возможных случая расположения вписанного угла относительно центра окружности.
Первый случай. Сторона вписанного угла проходит через центр окружности.
Соединим точку A с центром круга (точкой O). Получим равнобедренный треугольник AOB, в котором AO = OB, как радиусы одной окружности. Следовательно, ∠A = ∠B, как углы при основании равнобедренного треугольника.
Так как ∠AOC — внешний угол равнобедренного треугольника, то:
а так как углы A и B равны, то
| ∠B = | 1 | ∠AOC. |
| 2 |
Но ∠AOC — центральный угол, значит ∠AOC = 
| ∠ABC = ∠B = | 1 |  AC. AC. |
| 2 |
Второй случай. Центр окружности лежит между сторонами вписанного угла.
Проведём диаметр BD. Угол ABC разбился на два угла: ∠1 и ∠2.
Точка D разделяет дугу AC на две дуги: 

| ∠1 = | 1 |  AD и ∠2 = AD и ∠2 = | 1 |  DC. DC. |
| 2 | 2 |
Следовательно, весь угол ABC будет измеряться половиной дуги AC:
| ∠1 + ∠2 = | 1 |  AD + AD + | 1 |  DC DC |
| 2 | 2 |
| ∠ABC = | 1 |  AC. AC. |
| 2 |
Третий случай. Центр окружности лежит вне вписанного угла.
Проведём диаметр BD.
Но ∠ABD измеряется половиной дуги AD , а ∠CBD измеряется половиной дуги CD. Следовательно,
| ∠ABC = | 1 | ( AD — AD —  CD), CD), |
| 2 |
| ∠ABC = | 1 |  AC. AC. |
| 2 |
Видео:Геометрия. Теорема о вписанном углеСкачать

Следствия из теоремы
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги.
2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности.
Половина окружности содержит 180°, значит, угол, опирающийся на диаметр, содержит 90°.
Видео:Второй случай доказательства соотношения центрального и вписанного угломСкачать

Теорема с доказательством Вписанный угол измеряется половиной дуги, на которую он опирается.
Теорема 1. Вписанный угол измеряется половиной дуги, на которую он опирается.
Доказательство. Вписанный угол по отношению к центру окружности может располагаться так, что этот центр лежит: а) на одной из сторон угла; б) внутри угла; в) вне угла.
а) Пусть центр Q окружности принадлежит стороне угла LMN (рис. 7). Докажем, что величина угла LMN равна половине градусной меры дуги LN.
Угол LQN как внешний угол треугольника LQM равен сумме углов LMQ и QLM, Но эти углы равны друг другу как углы при основании равнобедренного треугольника LMQ.
Значит, , или . Поскольку градусные меры центрального угла LQN и дуги LN равны, то градусная мера в два раза меньшего вписанного угла равна
половине градусной меры дуги LN:
б) Пусть центр Q окружности лежит внутри угла LMN (рис. 8). Докажем, что величина угла LMN равна половине градусной меры дуги LN.
Проведем диаметр MP. Тогда луч MP разобьет угол LMN на два угла LMP и PMN, в каждом из которых одна сторона проходит через центр. Используя доказанное в а), получим:
Получили, что, как и в предыдущем случае, градусная мера угла LMN равна половине градусной меры дуги LN.
в) Пусть центр Q окружности лежит вне угла LMN (рис. 9). Докажем, что величина угла LMN и в этом случае равна половине градусной меры дуги LN.
Проведем диаметр MP. Тогда угол LMN равен разности углов LMP и NMP, в каждом из которых одна сторона проходит через центр. Используем доказанное в а) и получим:
Получили, что и в этом случае градусная мера угла LMN равна половине градусной меры дуги LN.
Таким образом, градусная мера вписанного угла равна половине градусной меры дуги, на которую этот угол опирается.
Следствие 1. Вписанные углы, опирающиеся на одну дугу, равны.
Следствие 2. Вписанный угол, опирающийся на диаметр, является прямым.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Углы, связанные с окружностью
 Вписанные и центральные углы Вписанные и центральные углы |
 Углы, образованные хордами, касательными и секущими Углы, образованные хордами, касательными и секущими |
 Доказательства теорем об углах, связанных с окружностью Доказательства теорем об углах, связанных с окружностью |
Видео:Углы, вписанные в окружность. 9 класс.Скачать

Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Видео:73. Теорема о вписанном углеСкачать

Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | ||||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды | |||||||||||||||||||||||||||||||||||
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр | |||||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника |  |
| Вписанный угол | |||||||||||||||||||||||||||||||||
| Окружность, описанная около прямоугольного треугольника | |||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |  | |
| Угол, образованный секущими, которые пересекаются вне круга |  |  | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  |  | |
| Угол, образованный касательной и секущей |  |  | |
| Угол, образованный двумя касательными к окружности |  |  |
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Видео:Геометрия 8 класс (Урок№27 - Теорема о вписанном угле.)Скачать  Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство 🔍 ВидеоПравильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать  Вписанный угол, общий случай.Скачать  Урок по теме ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ 8 КЛАСССкачать  70 Теорема о вписанном углеСкачать  Вписанные углы в окружностиСкачать  Доказательство того, что радиус перпендикулярен касательной | Окружность | ГеометрияСкачать  Секретная теорема из учебника геометрииСкачать  Вписанный угол равен половине центрального углаСкачать 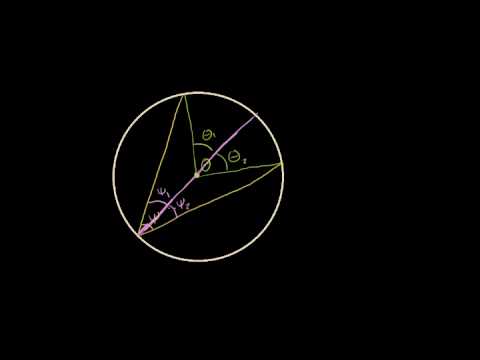 Теорема о свойстве вписанного угла 3 Хорды по одну сторону от центраСкачать  Всё про вписанные и центральные углы за 4 минуты | Борис Трушин |Скачать  Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать  Вписанный угол, частный случай.Скачать  |











































