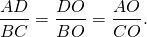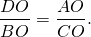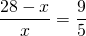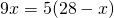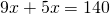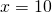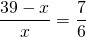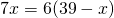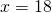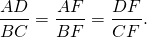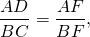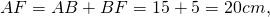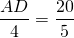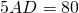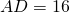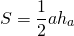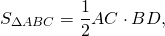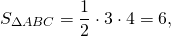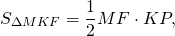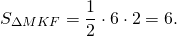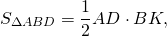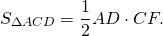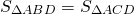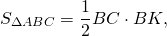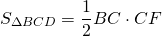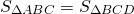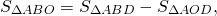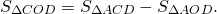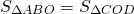Видео:Задача 15 ОГЭ: подобные треугольники в трапецииСкачать
We are checking your browser. mathvox.ru
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6dbc25da5813905d • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Видео:Как доказать У равнобедренной трапеции углы при основаниях равны и диагонали равныСкачать
Узнать ещё
Знание — сила. Познавательная информация
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать
Подобные треугольники в трапеции
Рассмотрим базовые задачи на подобные треугольники в трапеции.
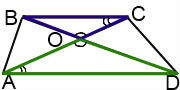
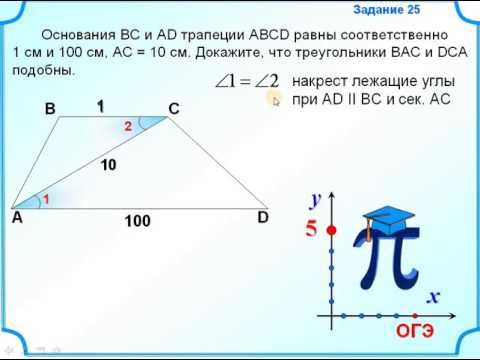
I. Точка пересечения диагоналей трапеции — вершина подобных треугольников.
Рассмотрим треугольники AOD и COB.
Визуализация облегчает решение задач на подобие. Поэтому подобные треугольники в трапеции выделим разными цветами.
1) ∠AOD= ∠ COB (как вертикальные);
2) ∠DAO= ∠ BCO (как внутренние накрест лежащие при AD ∥ BC и секущей AC).
Следовательно, треугольники AOD и COB подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
Одна из диагоналей трапеции равна 28 см и делит другую диагональ на отрезки длиной 5 см и 9 см. Найти отрезки, на которые точка пересечения диагоналей делит первую диагональ.
AO=9 см, CO=5 см, BD=28 см. BO =?, DO- ?
Доказываем подобие треугольников AOD и COB. Отсюда
Выбираем нужные отношения:
Пусть BO=x см, тогда DO=28-x см. Следовательно,
BO=10 см, DO=28-10=18 см.
Ответ: 10 см, 18 см.
Известно, что О — точка пересечения диагоналей трапеции ABCD (AD ∥ BC). Найти длину отрезка BO, если AO:OC=7:6 и BD=39 см.
Аналогичн0, доказываем подобие треугольников AOD и COB и
Пусть BO=x см, тогда DO=39-x см. Таким образом,
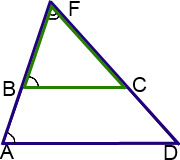
II. Продолжения боковых сторон трапеции пересекаются в точке.
Аналогично задаче I, рассмотрим треугольники AFD и BFC:
2) ∠ DAF= ∠ CBF (как соответственные углы при BC ∥ AD и секущей AF).
Следовательно, треугольники AFD и BFC подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
Продолжения боковых сторон AB и CD трапеции ABCD пересекаются в точке F. Меньшее основание BC равно 4 см, BF=5 см, AB=15 см. Найти большее основание трапеции.
Доказываем, треугольники AFD и BFC — подобны.
В следующий раз рассмотрим задачи на отношение площадей подобных треугольников.
Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать
Равновеликие треугольники
Равновеликие треугольники — это треугольники, которые имеют одинаковую площадь.
Равновеликие треугольники могут быть равными (так как равные треугольники имеют равные площади), но также могут иметь разные стороны и разные углы.
Например, треугольники ABC и MKF — равновеликие, так как их площади равны.
Можно заметить, что если сторону треугольника увеличить в k раз, а высоту, проведенную к этой стороне, уменьшить в k раз, то получим треугольник, равновеликий данному.
Равновеликие треугольники в треугольнике
Медиана делит треугольник на два равновеликих треугольника.
Равновеликие треугольники в трапеции
При пересечении диагоналей в произвольной трапеции ABCD образуется три пары равновеликих треугольников:
1) ∆ABD и ∆ACD,
1) Проведём в треугольниках ABD и ACD высоты BH и CF.
BK=CF (как высоты трапеции), следовательно,
3)
Так как площади треугольников ABD и ACD равны (по доказанному), то и
Таким образом, треугольники , образованные боковыми сторонами и диагоналями трапеции, имеют равные площади.
🔍 Видео
Подобные треугольники в трапеции. Площадь трапеции. Геометрия 8-9 классСкачать
Задание 25 Подобные треугольники в трапеции. Второй признак подобияСкачать
Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать
Геометрия 8 класс (Урок№5 - Теорема Фалеса)Скачать
КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать
8 класс, 6 урок, ТрапецияСкачать
Задание 25 Первый признак подобия треугольников в равнобокой трапецииСкачать
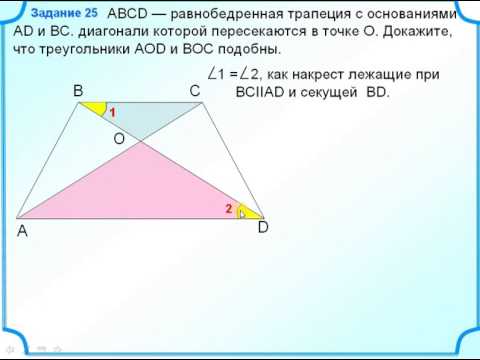
Доказательство равенства площадей треугольников в трапеции #геометрия #трапеция #железныйчеловекСкачать
Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать
Площадь параллелограмма треугольника и трапецииСкачать
8 класс, 15 урок, Площадь трапецииСкачать
Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать
Трапеция, решение задач. Вебинар | МатематикаСкачать
Средняя линия. Теорема о средней линии треугольникаСкачать
