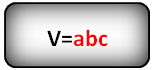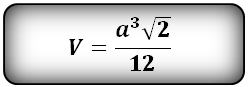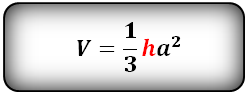Как узнать объем равнобедренного треугольника

Видео:Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

Свойства

Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1) P=2a+b

Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис.88.2) h_b=m_b=l_b=√(a^2-(b/2)^2 )=√(4a^2-b^2 )/2

Остальные две высоты равны друг другу и считаются через формулу с произведением разностей полупериметров и сторон, где приравнены боковые стороны. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a

Зная высоту, найти площадь равнобедренного треугольника можно, подставив полученное выражение в формулу, по которой площадь равна половине основания, умноженной на его высоту. S=hb/2=(b√(4a^2-b^2 ))/4

Углы в равнобедренном треугольнике распределяются следующим образом – углы при основании друг другу конгруэнтны, также как и боковые стороны, а в сумме все три угла дают 180 градусов, поэтому найти их можно двумя видами разности. α=(180°-β)/2 β=180°-2α

Если ни один из углов не дан, но есть все стороны, то можно воспользоваться теоремой косинусов, чтобы найти любой угол. cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 )

Медиана и биссектриса, опущенные на основание, вычисляются по формуле высоты, приведенной выше, а оставшиеся две медианы (равно как и две биссектрисы) равны друг другу, поскольку строятся на равных боковых сторонах. Вычислить медиану можно, упростив формулу произвольного треугольника. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

В формуле биссектрисы аналогично приравниваются боковые стороны, и ее становится возможным вычислить по упрощенной схеме. (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=(b√(a(2a+b) ))/(a+b)

Средняя линия равнобедренного треугольника, параллельная основанию, равна его половине, а средние линии, параллельные боковым сторонам, равны между собой и также равны половинам самих боковых сторон. (рис. 88.5) M_b=b/2 M_a=a/2

Радиус окружности, вписанной в равнобедренной треугольник, является производной формулы для произвольного треугольника, и рассчитать его можно, зная боковую сторону и основание. (рис. 88.6) r=b/2 √((2a-b)/(2a+b))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы и выглядит упрощенно следующим образом. (рис. 88.7) R=a^2/√(4a^2-b^2 )

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Все формулы объемов геометрических тел

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

1. Расчет объема куба

a — сторона куба

Формула объема куба, (V):

Видео:Площадь равнобедренного треугольникаСкачать

2. Найти по формуле, объем прямоугольного параллелепипеда

a , b , c — стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

Видео:Как распознать равнобедренный треугольник? #shortsСкачать

3. Формула для вычисления объема шара, сферы

R — радиус шара

По формуле, если дан радиус, можно найти объема шара, (V):

Видео:Определение угла равнобедренного треугольникаСкачать

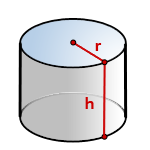
4. Как вычислить объем цилиндра ?

h — высота цилиндра

r — радиус основания

По формуле найти объема цилиндра, есди известны — его радиус основания и высота, (V):

Видео:Периметр равнобедренного треугольникаСкачать

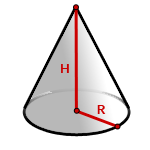
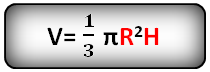
5. Как найти объем конуса ?

R — радиус основания

H — высота конуса

Формула объема конуса, если известны радиус и высота (V):

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

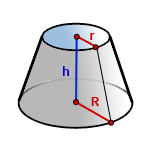
7. Формула объема усеченного конуса

r — радиус верхнего основания

R — радиус нижнего основания

h — высота конуса

Формула объема усеченного конуса, если известны — радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

Видео:Сможешь найти основание? Задача про медиану равнобедренного треугольникаСкачать

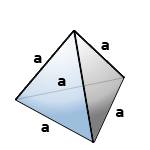
8. Объем правильного тетраэдра

Правильный тетраэдр — пирамида у которой все грани, равносторонние треугольники.

а — ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

Видео:Площадь равнобедренного треугольникаСкачать

9. Объем правильной четырехугольной пирамиды

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

a — сторона основания

h — высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (V):

Видео:Найдите гипотенузу равнобедренного прямоугольного треугольника, площадь которого равна 1Скачать

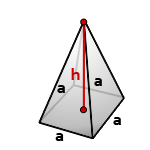
10. Объем правильной треугольной пирамиды

Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

a — сторона основания

h — высота пирамиды

Формула объема правильной треугольной пирамиды, если даны — высота и сторона основания (V):

Видео:Равнобедренный треугольник. 7 класс.Скачать

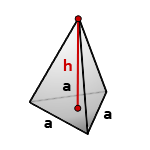
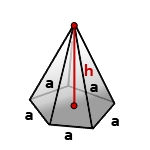
11. Найти объем правильной пирамиды

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

h — высота пирамиды

a — сторона основания пирамиды

n — количество сторон многоугольника в основании

Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

Видео:Нахождение сторон равнобедренного треугольникаСкачать

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

🌟 Видео

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

КАК НАЙТИ ВЫСОТУ ТРЕУГОЛЬНИКА? ЕГЭ и ОГЭ #shorts #егэ #огэ #математика #профильныйегэ #треугольникСкачать

№250. Найдите сторону равнобедренного треугольника, если две другие стороны равны: а) 7 см и 3 смСкачать

Свойства равнобедренного треугольника #огэ #математика #shortsСкачать

Площадь равнобедренного треугольника для фанатов Dark Souls и для всех остальных #огэ2023 #егэ2023Скачать

№228. Найдите углы равнобедренного треугольника, если один из его углов равен: а) 40°Скачать

Найдите площадь равнобедренного треугольника, основание которого равно 12 см, а боковая сторона 10.Скачать