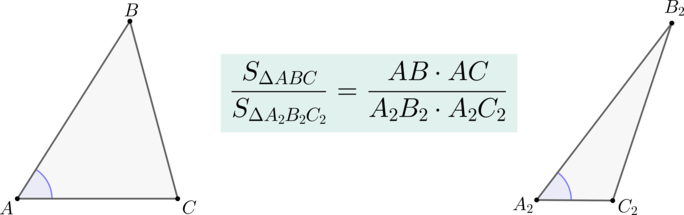Пусть А1А2. Аn — многоугольник, описанный около окружности; А1А2; А2А3; . Аn-1Аn — стороны многоугольника; ОА’1 = ОА’2 = . = ОА’n = r.
Соединим вершины многоугольника с центром окружности. Многоугольник разбит на n треугольников. Тогда:
Что и требовалось доказать.

задача №49
к главе «§14. Площади фигур».
- § 1. Правильные многоугольники
- Правильный многоугольник
- Окружность, описанная около правильного многоугольника
- Окружность, вписанная в правильный многоугольник
- Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
- Построение правильных многоугольников
- Задачи
- Ответы к задачам
- Площади многоугольников
- 🔍 Видео
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

§ 1. Правильные многоугольники
Правильный многоугольник
Вы знаете, как измеряются отрезки и как измеряются площади многоугольников. Вам известны формулы, по которым можно вычислить площади треугольника и некоторых четырёхугольников. А как вычислить длину окружности и площадь круга, если известен их радиус? Ответ на этот вопрос вы найдёте в этой главе. Но сначала нам предстоит познакомиться с красивыми геометрическими фигурами — правильными многоугольниками, вывести для них важные формулы, а затем уже с их помощью мы получим формулы длины окружности и площади круга.
Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
Примерами правильных многоугольников являются равносторонний треугольник и квадрат. На рисунке 306 изображены правильные пятиугольник, семиугольник и восьмиугольник.
Выведем формулу для вычисления угла αn правильного n-угольника. Сумма всех углов такого n-угольника равна (n — 2) • 180°, причём все его углы равны, поэтому
Окружность, описанная около правильного многоугольника
Напомним, что окружность называется описанной около многоугольника, если все вершины многоугольника лежат на этой окружности. Докажем теорему об окружности, описанной около правильного многоугольника.
| Около любого правильного многоугольника можно описать окружность, и притом только одну. |
Пусть А1А2А3. Аn — правильный многоугольник, О — точка пересечения биссектрис углов А1 и А2 (рис. 307).
Соединим точку О отрезками с остальными вершинами многоугольника и докажем, что ОА1 = ОА2 = . = ОАn. Так как ∠A1 = ∠A2, то ∠1 = ∠3, поэтому треугольник А1А2O равнобедренный: в нём ОА1 = ОА2. Треугольники А1A2О и А2А3О равны по двум сторонам и углу между ними (A1A2 = А3А2, А2O — общая сторона и ∠3 = ∠4), следовательно, ОА3 = ОА1. Точно так же можно доказать, что ОА4 = ОА2, ОА5 = ОА3 и т. д.
Итак, ОА1 = ОА2 = . = ОА n, т. е. точка О равноудалена от всех вершин многоугольника. Поэтому окружность с центром О и радиусом OA1 является описанной около многоугольника.
Докажем теперь, что описанная окружность только одна. Рассмотрим какие-нибудь три вершины многоугольника, например А1, А2, А3. Так как через эти точки проходит только одна окружность, то около многоугольника A1A2A3. An можно описать только одну окружность. Теорема доказана.
Окружность, вписанная в правильный многоугольник
Напомним, что окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности. Докажем теорему об окружности, вписанной в правильный многоугольник.
| В любой правильный многоугольник можно вписать окружность, и притом только одну. |
Пусть А 1А2. Аn — правильный многоугольник, О — центр описанной окружности (рис. 308). В ходе доказательства предыдущей теоремы мы установили, что ΔОА1А2 = ΔОА2А3 = . = ΔОАnА1, поэтому высоты этих треугольников, проведённые из вершины О, также будут равны: ОН1 = ОН2 =. = ОНn. Отсюда следует, что окружность с центром О и радиусом ОН1 проходит через точки H1, Н2, . Нn и касается сторон многоугольника в этих точках, т. е. эта окружность вписана в данный правильный многоугольник.
Докажем теперь, что вписанная окружность только одна.
Предположим, что наряду с окружностью с центром О и радиусом ОН1 есть и другая окружность, вписанная в многоугольник А1А2. Аn. Тогда её центр О1 равноудалён от сторон многоугольника, т. е. точка О1 лежит на каждой из биссектрис углов многоугольника и, следовательно, совпадает с точкой О пересечения этих биссектрис. Радиус этой окружности равен расстоянию от точки О до сторон многоугольника, т. е. равен ОН1. Таким образом, вторая окружность совпадает с первой. Теорема доказана.
| Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. |
| Окружность, вписанная в правильный многоугольник, касается сторон многоугольника в их серединах. |
Эта точка называется центром правильного многоугольника.
Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности
Пусть S — площадь правильного n-угольника, аn — его сторона, Р — периметр, а r и R — радиусы соответственно вписанной и описанной окружностей. Докажем сначала, что
Соединим центр данного многоугольника с его вершинами (см. рис. 308). Тогда многоугольник разобьётся на n равных треугольников, площадь каждого из которых будет равна 
Выведем далее формулы:
Для вывода этих формул воспользуемся рисунком 308. В прямоугольном треугольнике А1Н1О
Полагая в формуле (2) n = 3, 4 и 6, получим выражения для сторон правильного треугольника, квадрата и правильного шестиугольника:
Построение правильных многоугольников
Рассмотрим способы построения некоторых правильных многоугольников с помощью циркуля и линейки. Построения правильного треугольника и правильного четырёхугольника, т. е. квадрата, рассматривались ранее. Для построения правильных п-угольников при n > 4 обычно используется окружность, описанная около многоугольника.
Построить правильный шестиугольник, сторона которого равна данному отрезку.
Для решения задачи воспользуемся формулой (4). Пусть PQ — данный отрезок. Построим окружность радиуса PQ и отметим на ней произвольную точку А1 (рис. 309). Затем, не меняя раствора циркуля, построим на этой окружности точки А2, А3, А4, А5, А6 так, чтобы выполнялись равенства А1А2 = А2А3 = А3А4 = А4А5 = А5А6. Соединяя последовательно построенные точки отрезками, получим искомый правильный шестиугольник А1А2А3А4А5А6.
Для построения правильных многоугольников часто используется следующая задача:
Дан правильный n-угольник. Построить правильный 2n-угольник.
Пусть A1A2. An — данный правильный n-угольник. Опишем около него окружность. Для этого построим биссектрисы углов А1 и А2 и обозначим буквой О точку их пересечения. Затем проведём окружность с центром О радиуса ОА1 (см. рис. 307).
Для решения задачи достаточно разделить дуги А1А2, А2А3, . AnA1 пополам и каждую из точек деления В1, В2, . Вn соединить отрезками с концами соответствующей дуги (рис. 310, на этом рисунке n = 6). Для построения точек В1, В2, . Вn можно воспользоваться серединными перпендикулярами к сторонам данного n-угольника. На рисунке 310 таким способом построен правильный двенадцатиугольник A1B2А2B2. A6B6.
Применяя указанный способ, можно с помощью циркуля и линейки построить целый ряд правильных многоугольников, если построен один из них. Например, построив правильный четырёхугольник, т. е. квадрат, и пользуясь результатом задачи 2, можно построить правильный восьмиугольник, затем правильный шестнадцатиугольник и вообще правильный 2 k -угольник, где k — любое целое число, большее двух.
Рассмотренные примеры показывают, что многие правильные многоугольники могут быть построены с помощью циркуля и линейки. Оказывается, однако, что не все правильные многоугольники допускают такое построение. Доказано, например, что правильный семиугольник не может быть построен при помощи циркуля и линейки. Любопытно, что с помощью этих инструментов можно построить правильный семнадцатиугольник.
Задачи
1078. Верно ли утверждение: а) любой правильный многоугольник является выпуклым; б) любой выпуклый многоугольник является правильным? Ответ обоснуйте.
1079. Какие из следующих утверждений верны: а) многоугольник является правильным, если он выпуклый и все его стороны равны; б) треугольник является правильным, если все его углы равны; в) любой равносторонний треугольник является правильным; г) любой четырёхугольник с равными сторонами является правильным? Ответ обоснуйте.
1080. Докажите, что любой правильный четырёхугольник является квадратом.
1081. Найдите углы правильного n-угольника, если: а) n = 3; б) n = 5; в) n = 6; г) n = 10; д) n = 18.
1082 Чему равна сумма внешних углов правильного n-угольника, если при каждой вершине взято по одному внешнему углу?
1083. Сколько сторон имеет правильный многоугольник, если каждый его угол равен: а) 60°; б) 90°; в) 135°; г) 150°?
1084. Сколько сторон имеет правильный вписанный многоугольник, если дуга описанной окружности, которую стягивает его сторона, равна: а) 60°; б) 30°; в) 90°; г) 36°; д) 18°; е) 72°?
1085. Докажите, что серединные перпендикуляры к любым двум сторонам правильного многоугольника либо пересекаются, либо совпадают.
1086. Докажите, что прямые, содержащие биссектрисы любых двух углов правильного многоугольника, либо пересекаются, либо совпадают.
1087. На рисунке 311, а изображён квадрат, вписанный в окружность радиуса R. Перечертите таблицу в тетрадь и заполните пустые клетки (а4 — сторона квадрата, Р — периметр квадрата, S — его площадь, г — радиус вписанной окружности).
1088. На рисунке 311,6 изображён правильный треугольник, вписанный в окружность радиуса R. Перечертите таблицу в тетрадь и заполните пустые клетки (а3 — сторона треугольника, Р — периметр треугольника, S — его площадь, r — радиус вписанной окружности).
1089. Периметр правильного треугольника, вписанного в окружность, равен 18 см. Найдите сторону квадрата, вписанного в ту же окружность.
1090. Сечение головки газового вентиля имеет форму правильного треугольника, сторона которого равна 3 см. Каким должен быть минимальный диаметр круглого железного стержня, из которого изготовляют вентиль?
1091. Поперечное сечение деревянного бруска является квадратом со стороной 6 см. Найдите наибольший диаметр круглого стержня, который можно выточить из этого бруска.
1092. Около окружности описаны квадрат и правильный шестиугольник. Найдите периметр квадрата, если периметр шестиугольника равен 48 см.
1093. Около правильного треугольника описана окружность радиуса R. Докажите, что R = 2r, где r — радиус окружности, вписанной в этот треугольник.
1094. Найдите площадь S правильного га-угольника, если: а) n = 4, R = 3√2 см; б) n = 3, Р = 24см; в) n = 6, r = 9см; г) n = 8, r = 5√3 см.
1095. Расстояние между параллельными гранями шестигранной головки болта, основание которого имеет форму правильного шестиугольника, равно 1,5 см. Найдите площадь основания.
1096. Стороны правильного треугольника, квадрата и правильного шестиугольника равны друг другу. Найдите отношения площадей этих многоугольников.
1097. Найдите отношение площадей двух правильных шестиугольников — вписанного в окружность и описанного около неё.
1098. Выразите сторону, периметр и площадь правильного треугольника: а) через радиус вписанной окружности; б) через радиус описанной окружности.
1099. Правильный восьмиугольник A1A2. A8 вписан в окружность радиуса R. Докажите, что четырёхугольник А3А4А7А8 является прямоугольником, и выразите его площадь через R.
1100. С помощью циркуля и линейки в данную окружность впишите: а) правильный шестиугольник; б) правильный треугольник; в) квадрат; г) правильный восьмиугольник.
Ответы к задачам
1078. а) Да; б) нет.
1081. а) 60°; б) 108°; в) 120°; г) 144°; д) 160°.
1082. 360°. 1083. а) 3; б) 4; в) 8; г) 12.
1084. а) 6; б) 12; в) 4; г) 10; д) 20; е) 5.
1085. Указание. Воспользоваться тем, что серединный перпендикуляр к любой стороне правильного многоугольника проходит через центр описанной окружности.
1086. Указание. Воспользоваться тем, что биссектриса любого угла правильного многоугольника проходит через центр вписанной окружности.
1087.
1) R=3√2, r = 3, Р = 24, S = 36;
2) R = 2√2, а4 = 4, Р = 16, S = 16;
3) r = 2√2, а4 = 4√2, Р = 16√2, S = 32;
4) R = 3,5√2, r = 3,5, а4 = 7, S = 49;
5) R = 2√2, r = 2, а4 = 4, Р = 16.
1088.
1) r = 1,5, а3 = 3√3, Р = 9√3,
2) 
3) R = 4, а3 = 4√3, Р = 12√3, S = 12√3;
4)
5)
1094. a) 36 см 2 ; 6) 16√3 см 2 ; в) 162√3 см 2 ; r) ≈ 248,52 см 2 .
1095.
1098. a) 2√3r, 6√3r, 3√3r 2 ; б) √3R, 3√3R,
1100. в), г) Указание. Воспользоваться задачей 2, п. 113.
Видео:Геометрия Доказательство Площадь многоугольника, описанного около окружности равна произведению егоСкачать

Площади многоугольников
Можно сказать, что площадь многоугольника — это величина, обозначающая часть плоскости, которую занимает данный многоугольник. За единицу измерения площади принимают площадь квадрата со стороной (1) см, (1) мм и т.д. (единичный квадрат). Тогда площадь будет измеряться в см (^2) , мм (^2) соответственно.
Иными словами, можно сказать, что площадь фигуры — это величина, численное значение которой показывает, сколько раз единичный квадрат умещается в данной фигуре.
Свойства площади
1. Площадь любого многоугольника — величина положительная.
2. Равные многоугольники имеют равные площади.
3. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
4. Площадь квадрата со стороной (a) равна (a^2) .
Теорема: площадь прямоугольника
Площадь прямоугольника со сторонами (a) и (b) равна (S=ab) .
Доказательство
Достроим прямоугольник (ABCD) до квадрата со стороной (a+b) , как показано на рисунке:
Данный квадрат состоит из прямоугольника (ABCD) , еще одного равного ему прямоугольника и двух квадратов со сторонами (a) и (b) . Таким образом,
Определение
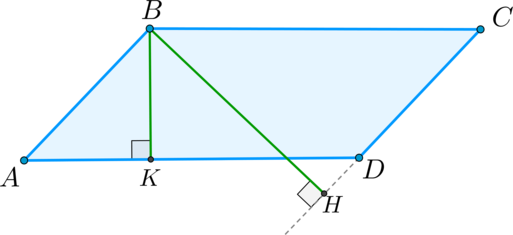
Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота (BK) падает на сторону (AD) , а высота (BH) — на продолжение стороны (CD) :
Теорема: площадь параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Проведем перпендикуляры (AB’) и (DC’) , как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма (ABCD) .
Тогда (AB’C’D) – прямоугольник, следовательно, (S_=AB’cdot AD) .
Заметим, что прямоугольные треугольники (ABB’) и (DCC’) равны. Таким образом,
Определение
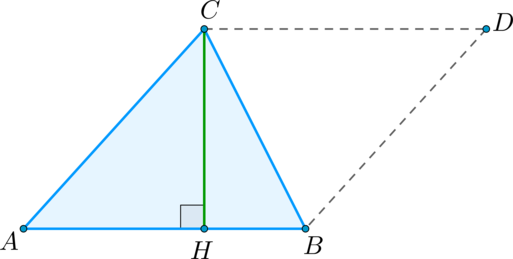
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
Пусть (S) – площадь треугольника (ABC) . Примем сторону (AB) за основание треугольника и проведём высоту (CH) . Докажем, что [S = dfracABcdot CH.] Достроим треугольник (ABC) до параллелограмма (ABDC) так, как показано на рисунке:
Треугольники (ABC) и (DCB) равны по трем сторонам ( (BC) – их общая сторона, (AB = CD) и (AC = BD) как противоположные стороны параллелограмма (ABDC) ), поэтому их площади равны. Следовательно, площадь (S) треугольника (ABC) равна половине площади параллелограмма (ABDC) , то есть (S = dfracABcdot CH) .
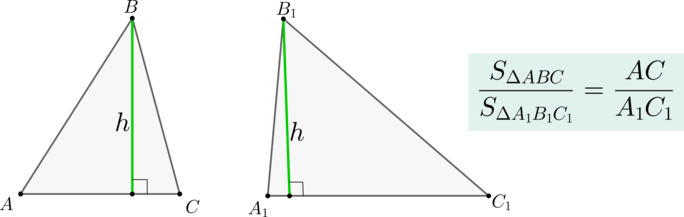
Теорема
Если два треугольника (triangle ABC) и (triangle A_1B_1C_1) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.
Теорема
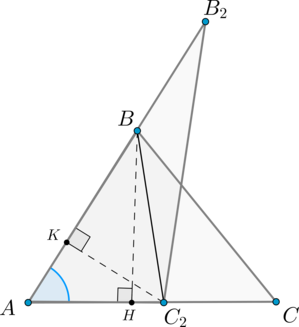
Если два треугольника (triangle ABC) и (triangle A_2B_2C_2) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
Доказательство
Пусть (angle A=angle A_2) . Совместим эти углы так, как показано на рисунке (точка (A) совместилась с точкой (A_2) ):
Проведем высоты (BH) и (C_2K) .
Треугольники (AB_2C_2) и (ABC_2) имеют одинаковую высоту (C_2K) , следовательно: [dfrac<S_><S_>=dfrac]
Треугольники (ABC_2) и (ABC) имеют одинаковую высоту (BH) , следовательно: [dfrac<S_><S_>=dfrac]
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Пусть (p) – полупериметр треугольника, (a) , (b) , (c) – длины его сторон, тогда его площадь равна [S_=sqrt
]
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
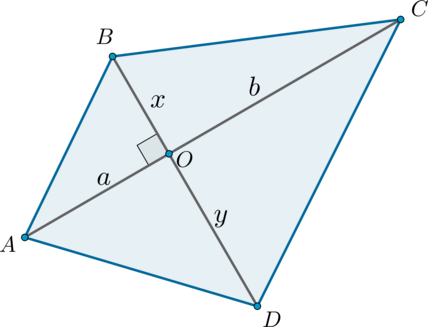
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Рассмотрим четырехугольник (ABCD) . Обозначим (AO=a, CO=b, BO=x, DO=y) :
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:
(begin S_=frac12ax+frac12xb+frac12by+frac12ay=frac12(ax+xb+by+ay)=\ frac12((a+b)x+(a+b)y)=frac12(a+b)(x+y)end)
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: [S_<text>=dfrac12 d_1cdot d_2]
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.
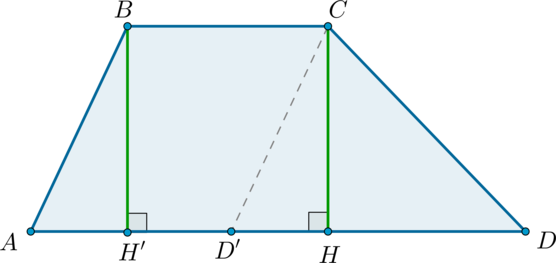
Теорема: площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство
Рассмотрим трапецию (ABCD) с основаниями (BC) и (AD) . Проведем (CD’parallel AB) , как показано на рисунке:
Тогда (ABCD’) – параллелограмм.
Проведем также (BH’perp AD, CHperp AD) ( (BH’=CH) – высоты трапеции).
Тогда (S_=BH’cdot AD’=BH’cdot BC, quad S_=dfrac12CHcdot D’D)
Т.к. трапеция состоит из параллелограмма (ABCD’) и треугольника (CDD’) , то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:
[S_=S_+S_=BH’cdot BC+dfrac12CHcdot D’D=dfrac12CHleft(2BC+D’Dright)=] [=dfrac12 CHleft(BC+AD’+D’Dright)=dfrac12 CHleft(BC+ADright)]
🔍 Видео
9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

110. Окружность, описанная около правильного многоугольникаСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Площадь многоугольника через радиус вписанной окружностиСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Геометрия 8 Площадь многоугольникаСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

8 класс, 10 урок, Понятие площади многоугольникаСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Площадь описанного многоугольникаСкачать

Площадь описанного многоугольникаСкачать

Площадь многоугольникаСкачать

Окружность, описанная около правильного многоугольника | Геометрия 7-9 класс #105 | ИнфоурокСкачать

Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать