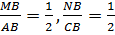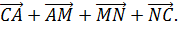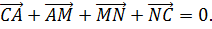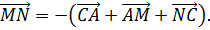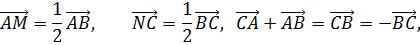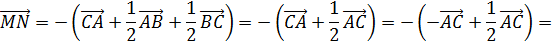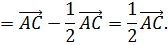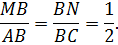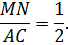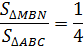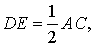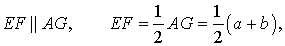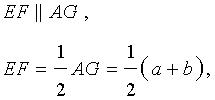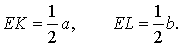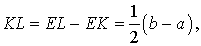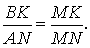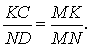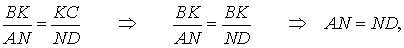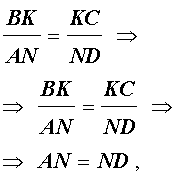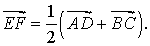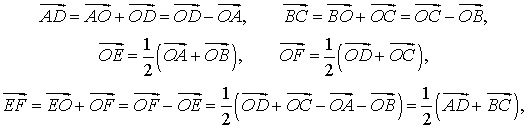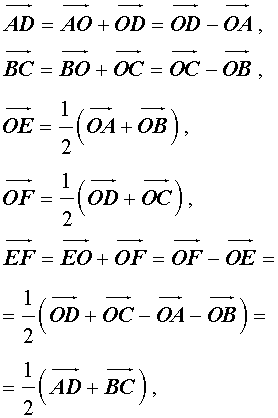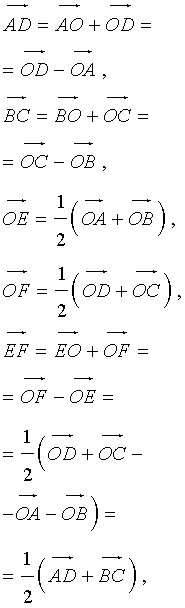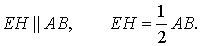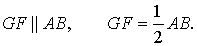Доказательство средней линии треугольника через вектора

Видео:Теорема о средней линии треугольникаСкачать

Ваш ответ

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

решение вопроса

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,937
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Геометрия 9 класс. Средняя линия трапецииСкачать

Средняя линия треугольника — свойства, признаки и формулы

Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.

Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Определение и признаки средней линии треугольника

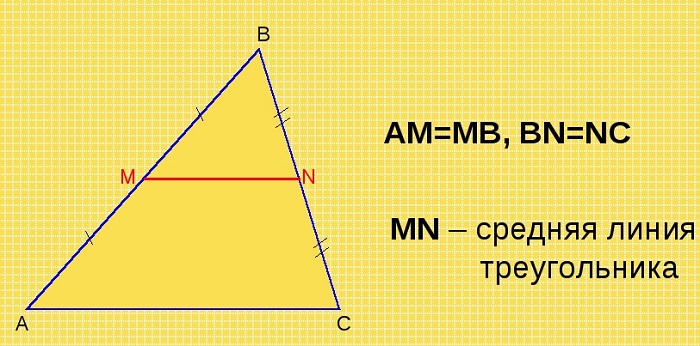
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.

Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.

Доказательство следует из теоремы Фалеса.

Видео:МАТЕМАТИКА | Средняя линия треугольникаСкачать

Теорема о средней линии треугольника

Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.

Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.

Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.

По определению, MN – средняя линия ΔABC.

Необходимо доказать, что MN II AC, MN = ½AC.

Доказательства

Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.

Следовательно, MN II AC.

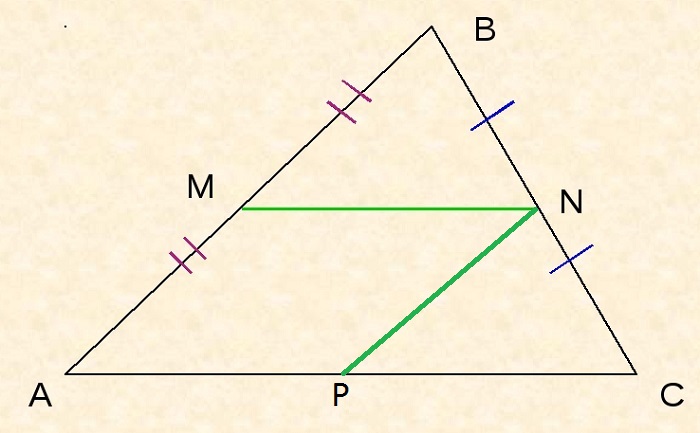
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.

Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.

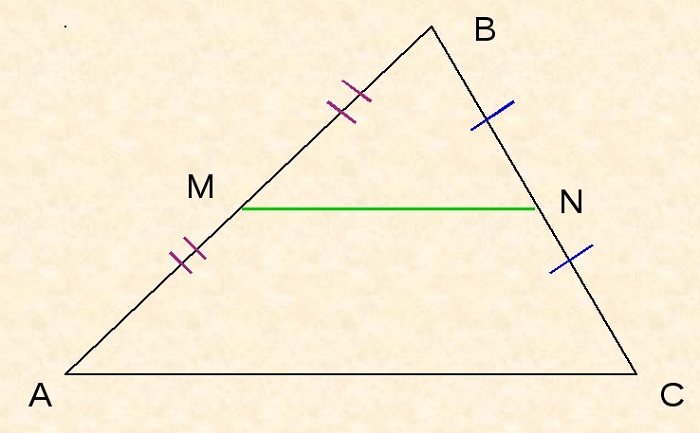
Рассматриваются треугольники MBN и ABC. В них угол B является общим,

По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.

Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.

Формула MN = ½AC следует из условий

поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.

Рассматривается сумма векторов

Поскольку в результате образуется замкнутая ломаная, то

Отсюда следует, что

Из последнего равенства следуют условия теоремы.

Видео:Теорема о средней линии трапецииСкачать

Следствия из теоремы с доказательствами

Следствие №1

Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.

По определению стороны AB и BC делятся пополам, поэтому

Из третьего признака подобия вытекает рассматриваемое свойство.

Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как

Следствие №2

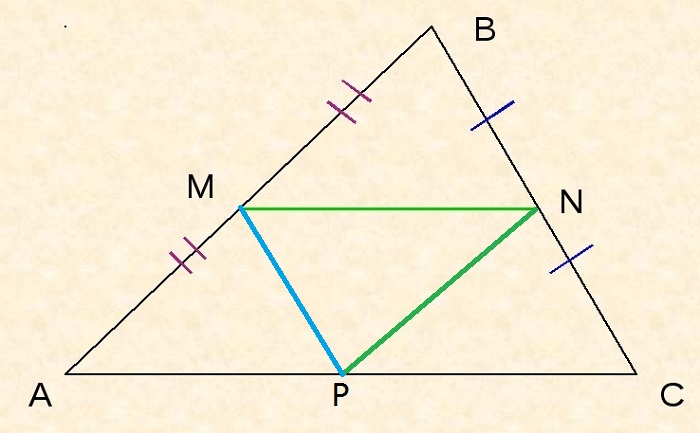
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.

Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.

Таким образом: ∠BNM = ∠BCA = ∠MPA.

Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.

Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.

Равенство остальных пар треугольников доказывается аналогично.

По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.

Видео:Теорема о средней линии треугольника. Доказательство. 8 класс.Скачать

Свойства средней линии треугольника

Теорема и следствия из неё составляют основные свойства средней линии треугольника.

Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.

Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.

Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.

Видео:8 класс, 25 урок, Средняя линия треугольникаСкачать

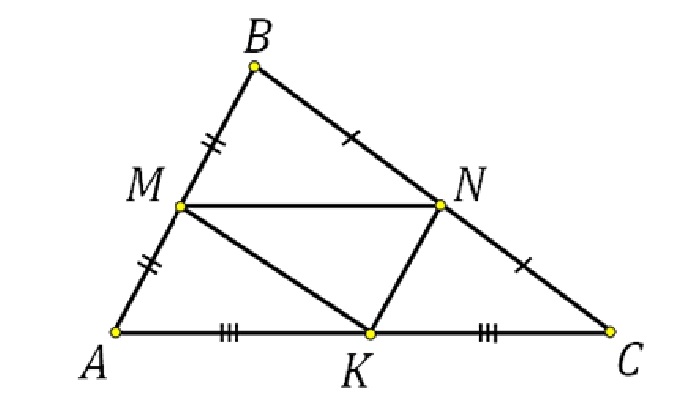
Средняя линия прямоугольного треугольника

Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.

Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.

Видео:умножение ВЕКТОРА на число + теорема о средней линии ТРАПЕЦИИСкачать

Пример решения задачи

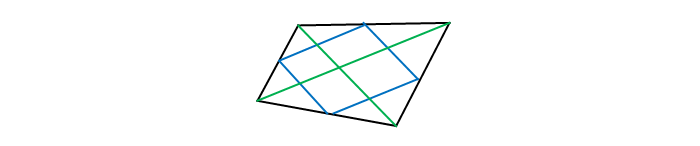
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.

Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.

Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.

Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.

Видео:Геометрия 9 класс (Урок№5 - Средняя линия трапеции.)Скачать

Средние линии

Средние линии треугольника

Средняя линия трапеции

Средние линии четырехугольников. Теорема Вариньона

Средние линии тетраэдра

Видео:Средняя линия трапеции и её свойства. Векторы на плоскости. Геометрия 8-9 классСкачать

Средние линии треугольника

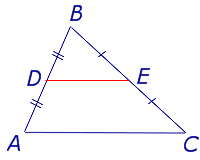
Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

На рисунке 1 средней линией является отрезок DE .

Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

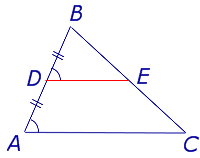
Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.

Первую часть утверждения 1 мы доказали.

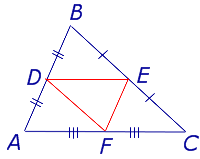
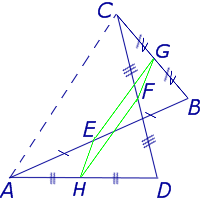
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).

Но поскольку AF = FC , то отсюда вытекает равенство

что и требуется доказать.

Доказательство утверждения 1 закончено.

• Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
• Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5 .

Видео:8 класс, 49 урок, Средняя линия трапецииСкачать

Средняя линия трапеции

Напомним, что трапецией трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

Параллельные стороны трапеции называют основаниями , а непараллельные стороны – боковыми сторонами трапеции.

Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

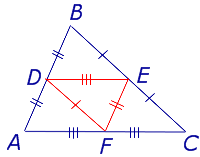
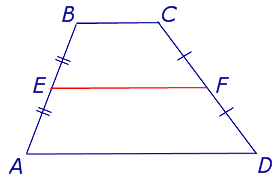
Определение . Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

На рисунке 5 средней линией трапеции является отрезок EF .

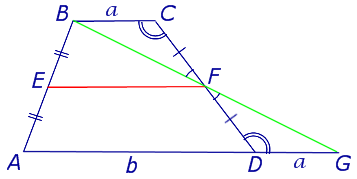
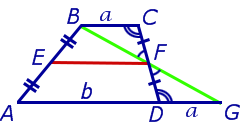
Утверждение 2 . Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

Доказательство . Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому

что и требовалось доказать.

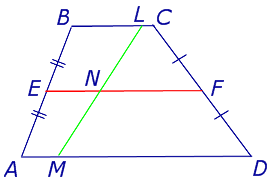
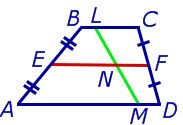
Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.

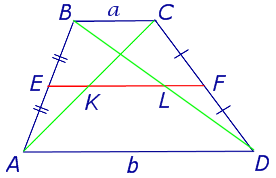
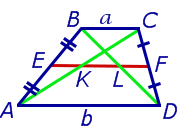
Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:

что и требовалось доказать.

Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

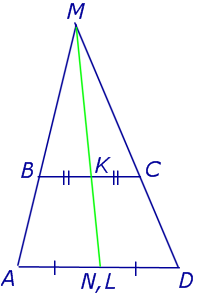
Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:

Из этих соотношений получаем:

откуда вытекает, что точки N и L совпадают. Доказательство завершено.

Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

Видео:Координаты вектора. 9 класс.Скачать

Средние линии четырехугольника. Теорема Вариньона

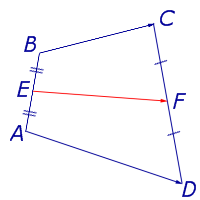
Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

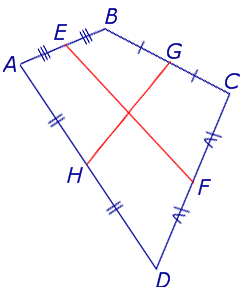
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

На рисунке 10 средние линии – это отрезки EF и GH .

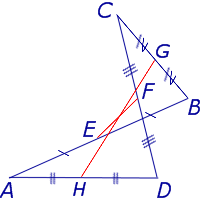
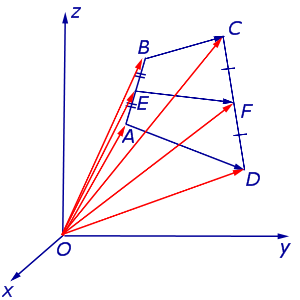
Замечание 1 . Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .

Замечание 2 . Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма параллелограмма .

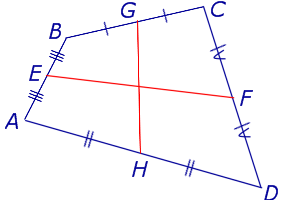
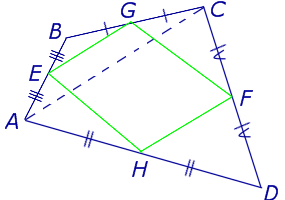
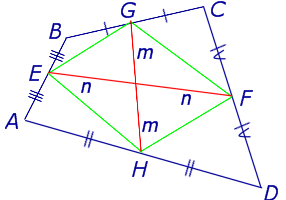
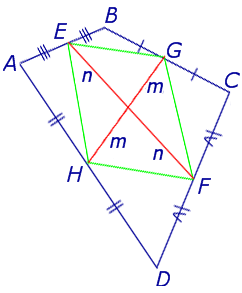
Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.

Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма признака параллелограмма признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.

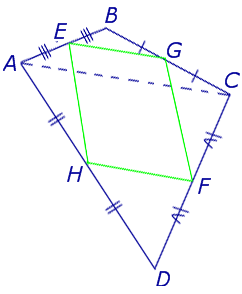
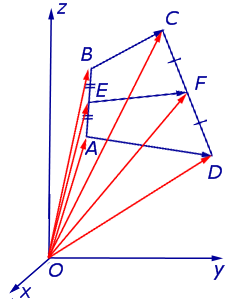
Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

Утверждение 5 . Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

Утверждение 6 . Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

что и требовалось доказать.

Следствие . Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией трапецией , а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Видео:Как доказать теорему о медианах треугольника с использованием методов векторной алгебры?Скачать

Средние линии тетраэдра

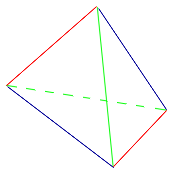
Тетраэдром называют произвольную треугольную пирамиду (рис.17).

У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер . На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых .

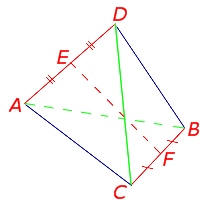
Определение . Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.

Утверждение 7 . Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

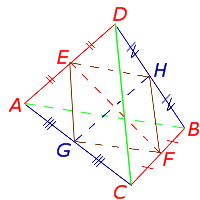
Доказательство . Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).

Заметим, что отрезок EH является средней линией треугольника ADB , поэтому

Определение . Точку пересечения средних линий тетраэдра называют центроидом тетраэдра .

Утверждение 8 . Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

🌟 Видео

Сложение векторов. 9 класс.Скачать

Угол между векторами. 9 класс.Скачать

ТРАПЕЦИЯ теорема о средней линии Атанасян 9 классСкачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Скалярное произведение векторов. 9 класс.Скачать