Доказательство равенства треугольников с биссектрисой

Теорема 1. Биссектриса при вершине треугольника делит противоположную сторону на две отрезки, пропорциональные сторонам, прилежащим к данной вершине. То есть если биссектриса при вершине A делит в точке D сторону BC на отрезки BD и CD (Рис.1), то имеет место следующее соотношение:

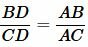(1)

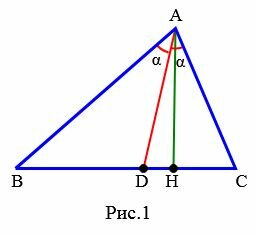Доказательство (метод площадей 1). Из вершины A опущена биссектриса AD. Построим вершину треугольника AH. Найдем площади треугольников ABD и ACD:

,

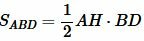(3)

.

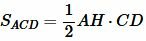(4)

Построим следующее соотношение

.

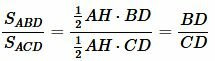(5)

С другой стороны, площадь треугольников ABD и ACD можно найти используя следующие формулы:

.

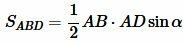(6)

.

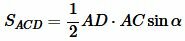(7)

Построим следующее соотношение используя формулы (6) и (7):

.

(8)

Из формул (5) и (8) получим соотношение (1).

Доказательство (метод площадей 2). С одной стороны, аналогично вышеизложенному имеем соотношение (5). Далее из точки D проведем вершины L и M для треугольников ABD и ACD (Рис.2).

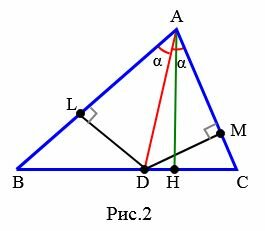Тогда площади треугольников ABD и ACD можно найти из формул:

,

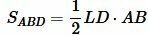(9)

.

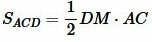(10)

Построим следующее соотношение

.

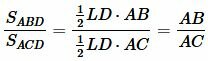(11)

Из формул (5) и (11) получим соотношение (1).

Доказательство (через теорему синусов). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.3):

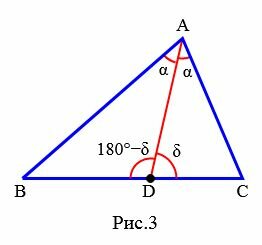Применяя теорему синусов для треугольников ABD и ACD можем записать:

,

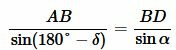(12)

.

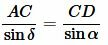(13)

Поделив (12) на (13) и учитывая, что ( small sin(180°-delta)=sin delta , ) (см. статью Формулы приведения тригонометрических функций онлайн) получим равенство (1).

Доказательство (через подобие треугольников). Рассмотрим треугольник ABC. Из точки A проведем биссектрису AD (Рис.4). Проведем перпендикуляры из вершин B и C на луч AD и обозначим точки пересечения через L и K.

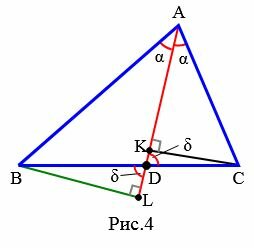Рассмотрим треугольники ABL и ACK. Эти треугольники подобны по двум углам (( small ∠ ALB= ∠ AKC ,;; ∠ BAL= ∠ CAK ) ). Тогда имеем:

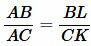(14)

Рассмотрим, далее, треугольники BLD и CKD. Они также подобны поскольку ( small ∠ BLD= ∠ CKD ,) а углы BDL и CDK равны так как они вертикальные. Тогда имеет место следующее соотношение:

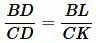(15)

Из равенств (14) и (15) получаем:

.

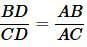Пример. Даны стороны треугольника ABC: AB=18, AC=6, BC=20. Найти отрезки, полученные делением биссектрисей большой стороны треугольника.

Решение. Поскольку напротив самой большой стороны треугольника находится вершина A, то бисскетриса AD делит сторону BC на отрезки BD и CD. Тогда имеем:

.

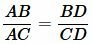(16)

Обозначим BD=x. Тогда CD=BC−x=20−x. Подставляя данные в уравнение (16), получим:

.

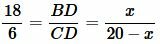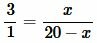(17)

Методом перекресного умножения упростим (17) и решим:

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Признаки равенства треугольников

О чем эта статья:

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Первый признак равенства треугольников

Конечно, равенство треугольников всегда можно доказать наложением одного треугольника на другой. Но, согласитесь, — это несерьезно. Какое может быть наложение, когда есть три теоремы и можно их доказать.

Давайте рассмотрим три признака равенства треугольников.

Теорема 1. Равенство треугольников по двум сторонам и углу между ними.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

При наложении △A₁B₁C₁ на △ABC вершина A₁ совмещается с вершиной A, и сторона A₁B₁ накладывается на сторону AB, AC — на сторону A₁C₁.

Сторона A₁B₁ совмещается со стороной AB, вершина B совпадает с вершиной B₁, сторона A₁С₁ совмещается со стороной AС, вершина C совпадает с вершиной C₁.

Значит, происходит совмещение вершин В и В₁, С и С₁.

Видео:Признаки равенства треугольников. 7 класс.Скачать

Второй признак равенства треугольников

Теорема 2. Равенство треугольников по стороне и двум прилежащим к ней углам.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Путем наложения △ABC на △A₁B₁C₁, совмещаем вершину А с вершиной A₁, вершины В и В₁ лежат по одну сторону от А₁С₁.

Тогда АС совмещается с A₁C₁, вершина C совпадает с C₁, поскольку мы знаем, что АС = A₁C₁.

AB накладывается на A₁B₁, поскольку мы знаем, что ∠A = ∠A₁.

CB накладывается на C₁B₁, поскольку мы знаем, что ∠C = ∠C₁.

Вершина B совпадает с вершиной B₁.

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Третий признак равенства треугольников

Теорема 3. Равенство треугольников по трем сторонам.

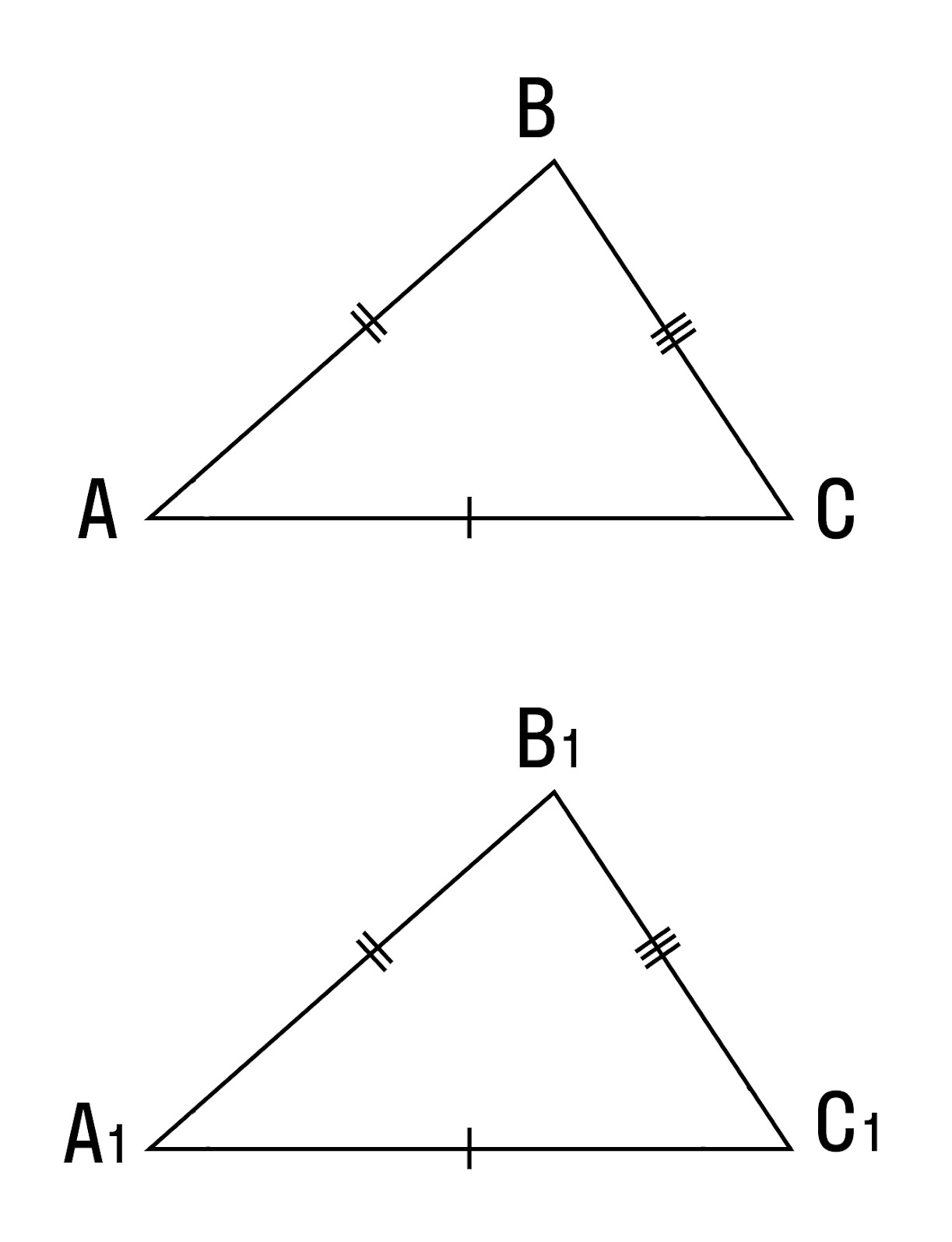
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство 3 признака равенства треугольников:

Приложим △ABC к △A₁B₁C₁ таким образом, чтобы вершина A совпала с вершиной A₁, вершина B — с вершиной B₁, вершина C и вершина C₁ лежат по разные стороны от прямой А₁В₁.

Кроме трех основных теорем, запомните еще несколько признаков равенства треугольников.

Равны ли треугольники, можно определить не только по сторонам и углам, но и по высоте, медиане и биссектрисе.

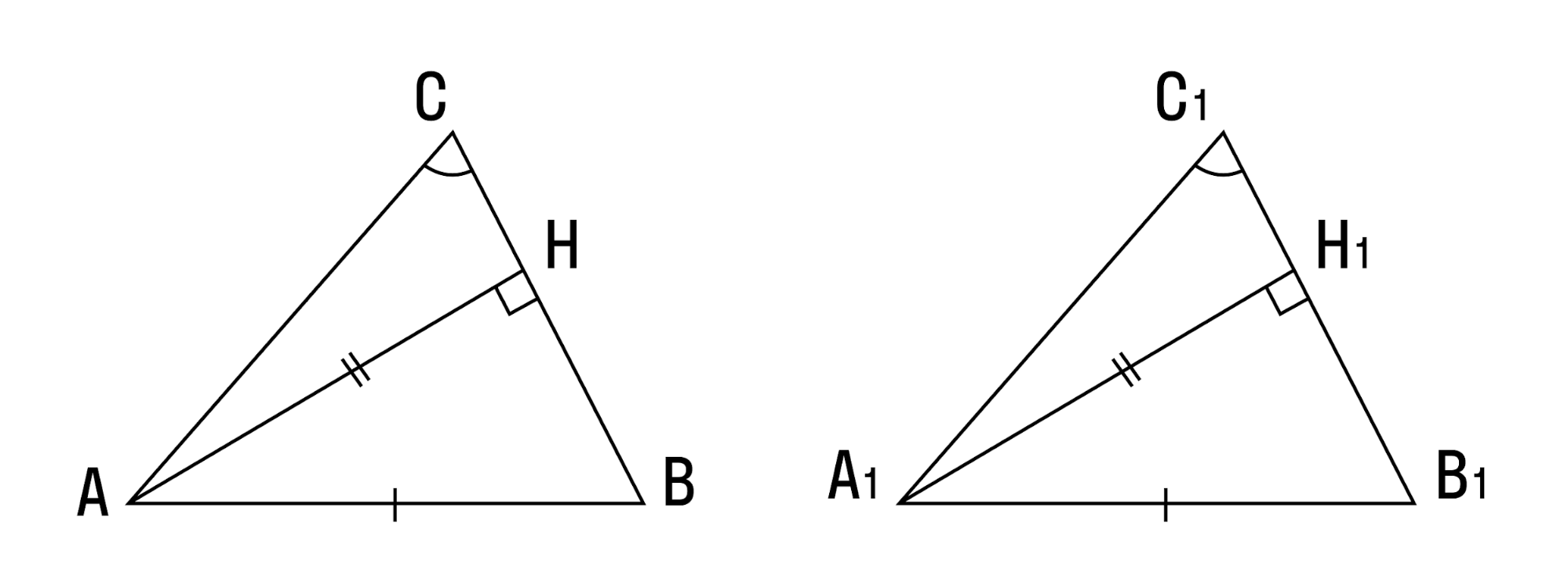
1. Если угол, сторона, противолежащая этому углу, и высота, опущенная на другую сторону, одного треугольника соответственно равны углу, стороне и высоте другого треугольника — такие треугольники равны.
   
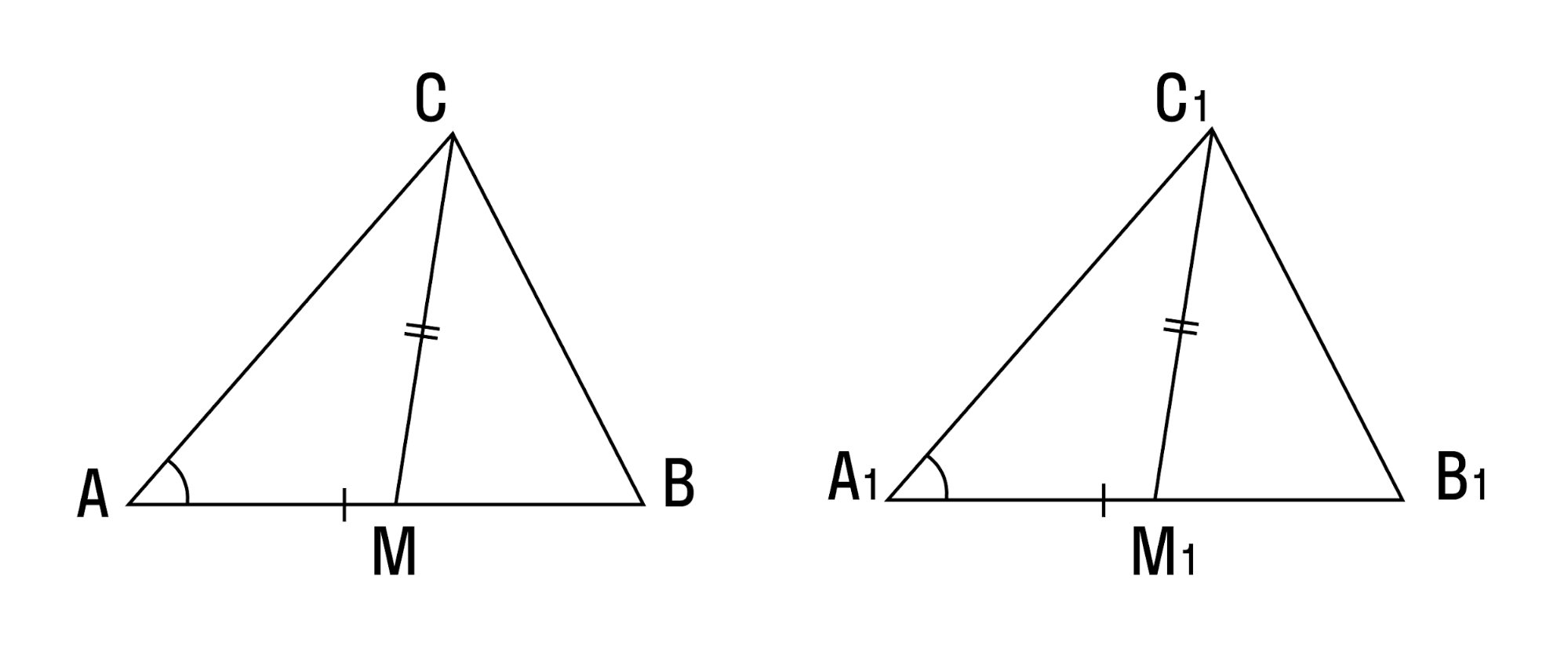
2. Если две стороны и медиана, заключенная между ними, одного треугольника соответственно равны двум сторонам и медиане другого треугольника — такие треугольники равны.
   
3. Если сторона и две медианы, проведенные к двум другим сторонам, одного треугольника соответственно равны стороне и двум медианам другого треугольника — такие треугольники тоже равны.
   
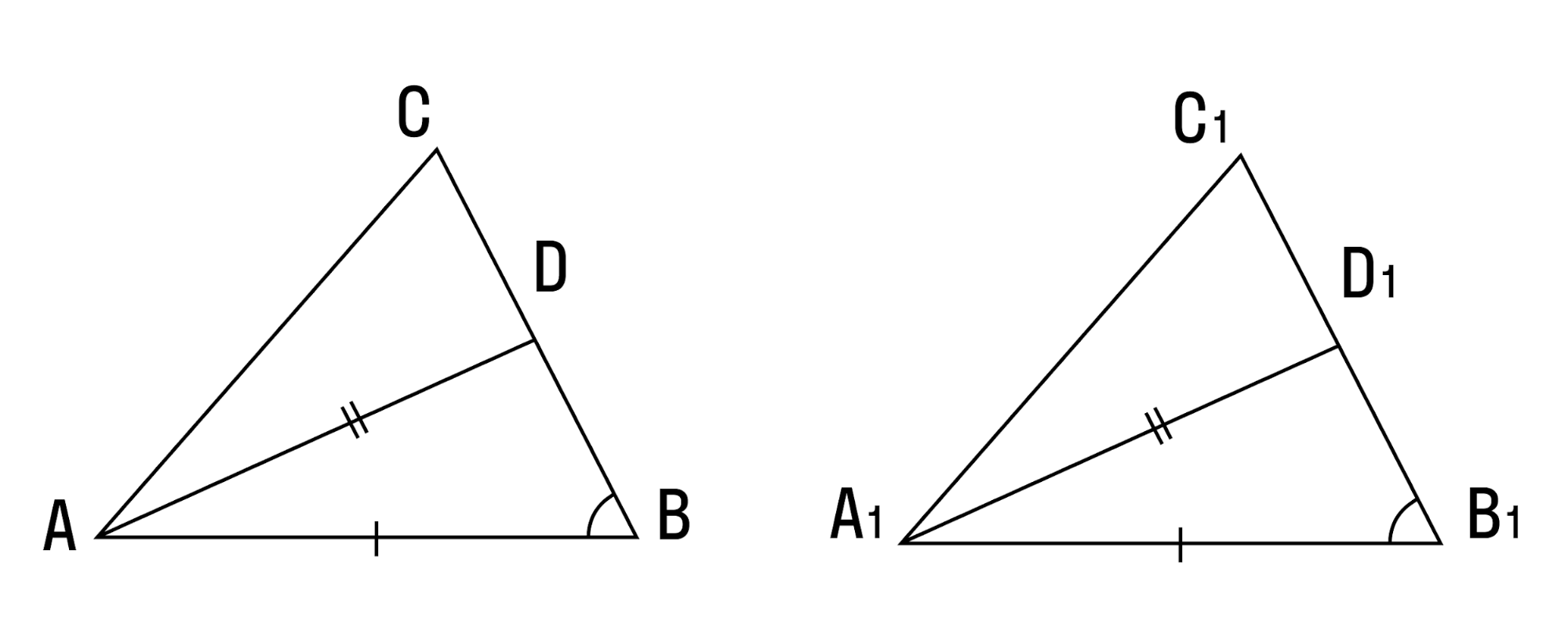
4. Если две стороны и биссектриса, заключенная между ними, одного треугольника соответственно равны двум сторонам и биссектрисе другого треугольника — вы уже догадались сами: эти ребята равны.
   
5. Два треугольника равны, если сторона, медиана и высота, проведенные к другой стороне, одного треугольника соответственно равны стороне, медиане и высоте другого треугольника.
   

Как видите, доказать равенство треугольников можно по множеству признаков и десятком способов. Три признака равенства треугольников — основные. Все остальные способы также стоит запомнить, ведь треугольник — только с виду простая фигура.

Видео:Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Признаки равенства треугольников с использованием медианы, биссектрисы и высоты

Признаки равенства треугольников с использованием медианы, биссектрисы и высоты. Решетников Михаил Сергеевич, Харютченко Данил Александрович. Муниципальный этап.

Видео:Третий признак равенства треугольников (доказательство) - геометрия 7 классСкачать

Скачать:

Видео:Первый признак равенства треугольников. 7 класс.Скачать

Предварительный просмотр:

МУНИЦИПАЛЬНЫЙ ЭТАП XI ВСЕРОССИЙСКОГО ДЕТСКОГО КОНКУРСА
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИХ И ТВОРЧЕСКИХ РАБОТ
«ПЕРВЫЕ ШАГИ В НАУКЕ»

Секция: информационные технологии; математика;

Тема: Признаки равенства треугольников с использованием медианы, биссектрисы и высоты

Авторы: Решетников Михаил Сергеевич, МОУ «Октябрьская СОШ им. Ю. Чумака», 8 класс

Харютченко Данил Александрович, МОУ «Октябрьская СОШ им. Ю. Чумака», 8 класс

Научный руководитель: Шевченко Елена Михайловна, учитель математики МОУ «Октябрьская СОШ им. Ю. Чумака»

Место выполнения работы: Белгородская область, Белгородский район, поселок Октябрьский

Признаки равенства треугольников с использованием медианы, биссектрисы и высоты

Треугольник – одна из самых простых и загадочных геометрических фигур. Вот уже два с половиной тысячелетия открываются его новые и новые свойства. Со времен «Начал» Евклида геометрия строится на основе трех признаков равенства треугольников. Исходя из того, что в треугольнике выделяют шесть основных элементов: три внутренних угла и три соответственно противолежащие им стороны, равенство треугольников устанавливается по равенству трех из шести элементов. Три следующих признака являются фундаментом геометрии:

1. по двум сторонам и углу между ними;
2. по стороне и прилежащим к ней углам;
3. по трём сторонам.

Эти признаки отличаются простотой формулировки и часто применяются при решении задач базового уровня. Рассматривая более сложные задачи, приходится фактически «изобретать велосипед», дважды или трижды применять известные признаки, конструируя из них решение. Это приводит к следующему выводу: известных трех признаков не всегда достаточно.

Если учесть, что для каждого треугольника однозначно определяются три медианы, три биссектрисы и три высоты, то число элементов треугольника увеличивается до 15. В связи с этим возникает следующая гипотеза: наряду с основными тремя признаками равенства треугольников можно сформулировать и доказать новые признаки равенства треугольников с использованием медианы, биссектрисы и высоты, знание которых поможет в решении многих геометрических задач.

Объектом данного исследования является треугольник и его элементы, в том числе медианы, биссектрисы и высоты; предмет исследования – признаки равенства треугольников.

• сформулировать и доказать новые признаки равенства треугольников;

• обосновать эффективность применения новых признаков равенства треугольников при решении геометрических задач.

• проанализировать определения и свойства медианы, биссектрисы и высоты;
• выявить зависимость между равенством отдельных элементов и равенством треугольников;
• определить типы геометрических задач, при решении которых целесообразно применение полученных признаков.

В работе применялись методы научного исследования: анализ, сравнение, математическое моделирование.

Для доказательства новых признаков равенства треугольников использовались только первый, второй и третий признаки равенства треугольников, что обеспечивает простоту доказательства и доступность данной работы для широкого круга школьников.

📸 Видео

Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Свойство биссектрисы треугольника с доказательствомСкачать

Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Первый признак равенства треугольников. Доказательство. Задачи по рисункам.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Геометрия 7 класс (Урок№12 - Медианы треугольника. Биссектрисы треугольника. Высоты треугольника.)Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Второй признак равенства треугольников. 7 класс.Скачать

Второй признак равенства треугольников. Доказательство. Задачи по рисунку. Геометрия 7Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать