Доказать что прямая а параллельна прямой б и найти угол 1 (7 видео)

По данным рисунка Докажите что Прямые А и Б параллельны Найдите угол 1?

Геометрия | 5 — 9 классы

По данным рисунка Докажите что Прямые А и Б параллельны Найдите угол 1.

Угол 5 и угол 4 — односторонние.

Они в сумме дают нам 180 градусов ( 42 + 138 = 180) Следовательно прямые параллельны.

Содержание

Даны прямые а, в, с?
Докажите что через данную точку не лежащую на данной прямой проходит прямая параллельная данной?
1)докажите что прямые a и b параллельны , используя данные рисунки2)найдите x?
Дана прямая, параллельная некоторой плоскости?
Определи по данным рисунка , если ли там параллельные прямые?
По данным рисунка докажите что отрезки АВ и СD параллельны?
На рисунке AD параллельна BE, AC = AD и BC = BE?
На рисунке прямые a и b параллельны, угол 1 = 55°?
Докажите, что прямые n и k на рисунке параллельны, если угол 2 = углу 1?
Параллельные прямые c и d пересечены прямой a?
Прямая линия. Признаки параллельности прямых линий.
Доказать что прямая а параллельна прямой б и найти угол 1
🎥 Видео

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Даны прямые а, в, с?

Даны прямые а, в, с.

Если а перпендикулярна с, в перпендикулярна с, то докажите параллельность прямых а и в.

Видео:№45. Прямая а параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости параллелограмма.Скачать

Докажите что через данную точку не лежащую на данной прямой проходит прямая параллельная данной?

Докажите что через данную точку не лежащую на данной прямой проходит прямая параллельная данной.

Видео:№186. На рисунке 106 прямые а и b пересечены прямой с. Докажите, что a||b, если: a)∠1=37°Скачать

1)докажите что прямые a и b параллельны , используя данные рисунки2)найдите x?

1)докажите что прямые a и b параллельны , используя данные рисунки

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Дана прямая, параллельная некоторой плоскости?

Дана прямая, параллельная некоторой плоскости.

Докажите что через любую точку этой плоскости проходит прямая параллельная данной прямой.

Видео:№ 186 - Геометрия 7-9 класс АтанасянСкачать

Определи по данным рисунка , если ли там параллельные прямые?

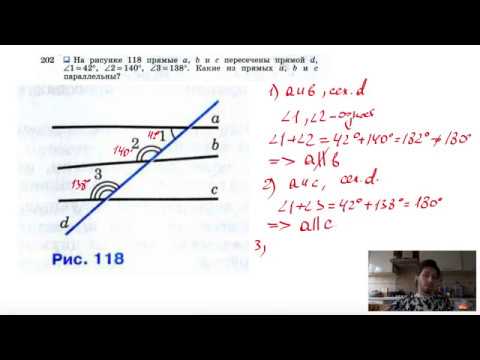
Видео:№202. На рисунке 116 прямые а, b и с пересечены прямой d, ∠1=42°, ∠2=140°, ∠3=138°. Какие из прямыхСкачать

По данным рисунка докажите что отрезки АВ и СD параллельны?

По данным рисунка докажите что отрезки АВ и СD параллельны.

Видео:Параллельные прямые (задачи).Скачать

На рисунке AD параллельна BE, AC = AD и BC = BE?

На рисунке AD параллельна BE, AC = AD и BC = BE.

Докажи, что угол DCE прямой.

Видео:№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

На рисунке прямые a и b параллельны, угол 1 = 55°?

На рисунке прямые a и b параллельны, угол 1 = 55°.

Видео:Геометрия 7 класс (Урок№19 - Признаки параллельности прямых.)Скачать

Докажите, что прямые n и k на рисунке параллельны, если угол 2 = углу 1?

Докажите, что прямые n и k на рисунке параллельны, если угол 2 = углу 1.

Видео:№200. На рисунке 115 AD||p и PQ||BC. Докажите, что прямая р пересекает прямые АВ, АЕ, АС, ВС и PQ.Скачать

Параллельные прямые c и d пересечены прямой a?

Параллельные прямые c и d пересечены прямой a.

По данным рисунка найдите угол a.

Вы перешли к вопросу По данным рисунка Докажите что Прямые А и Б параллельны Найдите угол 1?. Он относится к категории Геометрия, для 5 — 9 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Геометрия. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

KF = ON = 3 TK = KF ; FK + KT = FT = 3 + 3 = 6 ; KO = FN = 7 ; FN = NE ; FN + NE = FE ; 7 + 7 = 14 ; FE = TS = 14 ; TF = SE = 6.

Видео:№57. Прямая а параллельна одной из двух параллельных плоскостей. Докажите, что прямаяСкачать

Прямая линия. Признаки параллельности прямых линий.

Если две произвольные прямые AB и СD пересечены третьей прямой MN, то образовавшиеся при этом углы получают попарно такие названия:

соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;

внутренние накрест лежащие углы: 3 и 5, 4 и 6;

внешние накрест лежащие углы: 1 и 7, 2 и 8;

внутренние односторонние углы: 3 и 6, 4 и 5;

внешние односторонние углы: 1 и 8, 2 и 7.

Описанные углы видны на рисунке:

Теорема.

Если две параллельные прямые пересечены третьей прямой, то сформировавшиеся:

1. внутренние накрест лежащие углы одинаковы;

2. внешние накрест лежащие углы одинаковы;

3. соответственные углы одинаковы;

4. сумма внутренних односторонних углов будет 2d = 180 0 ;

5. сумма внешних односторонних углов будет 2d = 180 0 ;

Данную теорему иллюстрирует рисунок:

Имеются две параллельные прямые AB и СD, их пересекает третья прямая MN.

1. ∠ 4 = ∠ 6 и ∠ 3 = ∠ 5;

2. ∠ 2 = ∠ 8 и ∠ 1 = ∠ 7;

3. ∠ 2 =∠ 6, ∠ 1 = ∠ 5, ∠ 3 = ∠ 7, ∠ 4 = ∠ 8;

4. ∠ 3 + ∠ 6 = 2d и ∠ 4 + ∠ 5 = 2d;

5. ∠ 2 + ∠ 7 = 2d и ∠ 1 + ∠ 8 = 2d.

1. Из середины E того отрезка прямой MN, который размещается между параллельными прямыми, прочертим на СD перпендикуляр EK и продолжим его до пересечения с AB в точке L. Так как перпендикуляр к одной из параллельных есть также и перпендикуляр к другой параллельной, то образовавшиеся при этом треугольники (заштрихованные на чертеже) — оба прямоугольные. Они одинаковы, потому что в них по равной гипотенузе и по одинаковому острому углу при точке E. Из равенства треугольников получаем, что внутренние накрест лежащие углы 4 и 6 одинаковы. Два прочих внутренних накрест лежащих угла 3 и 5 одинаковы, как дополнения до 2d к одинаковым углам 4 и 6 (как смежные с 4 и 6).

2. Внешние накрест лежащие углы равны соответственно внутренним накрест лежащим углам, как углы вертикальные.

Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.

Следовательно, ∠ 2 =∠ 8.

3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.

4. Сумма внутренних односторонних углов 3 и 6 будет 2d, потому что сумма смежных углов 3 и 4 равна 2d = 180 0 , а ∠ 4 можно заменить идентичным ему ∠ 6. Также убедимся, что сумма углов 4 и 5 равна 2d.

5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам, как углы вертикальные.

Из выше доказанного обоснования получаем обратные теоремы.

Когда при пересечении двух прямых произвольной третьей прямой получим, что:

1. Внутренние накрест лежащие углы одинаковы;

или 2. Внешние накрест лежащие углы одинаковые;

или 3. Соответственные углы одинаковые;

или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ;

или 5. Сумма внешних односторонних равна 2d = 180 0 ,

Видео:№36. Прямая с пересекает прямую а и не пересекает прямую b, параллельную прямой а.Скачать

Доказать что прямая а параллельна прямой б и найти угол 1

305. Параллельны ли изображённые на рисунке 212 прямые a и b , если:

3) ∠ 4 = 125°, ∠ 6 = 55°;

4) ∠ 2 = 35°, ∠ 5 = 146°;

5) ∠ 1 = 98°, ∠ 6 = 82°;

6) ∠ 1 = 143°, ∠ 7 = 37°?

306. На каких из рисунков 213, а – г прямые m и n параллельны?

307. На рисунке 214 укажите все пары параллельных прямых.

308. На рисунке 215 укажите параллельные прямые, если ∠ 1 = 53°, ∠ 2 = 128°, ∠ 3 = 127°.

309. На рисунке 216 AB = BC , CD = DK . Докажите, что AB ‖ DK .

310. На рисунке 217 AK — биссектриса угла BAC , AM = MK . Докажите, что MK ‖ AC .

311. На рисунке 218 ∠ ACB = ∠ ACD , AD = CD . Докажите, что BC ‖ AD .

312. В треугольнике ABC известно, что AB = BC , ∠ A = 60°, ∠ BCD — смежный с ∠ ACB , CM — биссектриса угла BCD . Докажите, что AB ‖ CM .

313. Отрезки AB и CD пересекаются в точке O и делятся этой точкой пополам. Докажите, что AC ‖ BD .

314. На рисунке 219 AB = CD , BC = AD . Докажите, что AB ‖ CD .

315. Известно, что некоторая прямая m пересекает прямую a (рис. 220). Пересекает ли прямая m прямую b ?

316. Каково взаимное расположение прямых CD и EF на рисунке 221?

317. Угол ABC равен 60°, а угол BCD — 120°. Можно ли утверждать, что прямые AB и CD параллельны?

318. Угол между прямыми a и c равен углу между прямыми b и c . Можно ли утверждать, что прямые a и b параллельны?

319. Четыре угла, образованные при пересечении прямых a и b прямой c , равны по 40°, а любой из остальных четырёх углов — 140°. Можно ли утверждать, что прямые a и b параллельны?

320. Прямая пересекает биссектрису BM треугольника ABC в точке O , являющейся серединой отрезка BM , а сторону BC — в точке K . Докажите, что если OK ⊥ BM , то MK ‖ AB .

321. Отрезки AM и CK — медианы треугольника ABC . На продолжении отрезка AM за точку M отложен отрезок MF , а на продолжении отрезка CK за точку K — отрезок KD так, что MF = AM , KD = CK . Докажите, что точки B , D и F лежат на одной прямой.

Упражнения для повторения

322. Луч OC разбивает угол AOB на два угла так, что ∠ AOC : ∠ BOC = 3 : 5. Найдите угол между лучом OC и биссектрисой угла, смежного с углом AOB , если угол BOC на 42° больше угла AOC .

323. На рисунке 222 AB = BC , ∠ ABK = ∠ CBM . Докажите, что BM = BK .

324. Равнобедренные треугольники ABC и ADC имеют общее основание AC . Прямая BD пересекает отрезок AC в точке E . Докажите, что AE = EC .

Наблюдайте, рисуйте, конструируйте, фантазируйте

325. Приведите пример, когда общей частью (пересечением) треугольника и четырёхугольника является восьмиугольник.

Когда сделаны уроки

Пятый постулат Евклида

В § 6 вы узнали, что в качестве аксиом выбирают очевидные утверждения. Тогда почему бы, например, теоремы 1.1 и 5.1 не включить в список аксиом, ведь они тоже очевидны? Ответ на этот вопрос понятен: если какое-то утверждение можно доказать с помощью аксиом, то это утверждение — теорема, а не аксиома. С этих позиций очень поучительна история, связанная с пятым постулатом Евклида

V постулат. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны от секущей, с которой эта сумма меньше двух прямых углов ( рис. 223 ).

Можно показать, что пятый постулат и сформулированная нами в § 13 аксиома параллельности прямых равносильны, т. е. из постулата следует аксиома и наоборот — из аксиомы следует постулат.

Более двадцати веков многие учёные пытались доказать пятый постулат, т. е. вывести его из других аксиом Евклида. Лишь в начале XIX в. несколько математиков независимо друг от друга пришли к выводу: утверждение, что через данную точку, не лежащую на данной прямой, мож но провести только одну прямую, параллельную данной , является аксиомой.

Вам может показаться, что в этом выводе ничего особенного нет: присоединяем аксиому параллельности к уже существующему списку аксиом-правил, а дальше доказываем теоремы.

Однако если в футболе добавить только одно правило, например разрешить полевым игрокам играть и руками, то мы получим совершенно новую игру.

Если пятый постулат — это правило, которое мы принимаем, а не теорема, то его можно заменить противоположным утверждением.

Так и поступил Н.И. Лобачевский. Он заменил лишь одно правило — аксиому параллельности прямых — следующим: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, не пересекающие данную. Новая аксиома позволила построить новую геометрию — неевклидову.