Для того чтобы цилиндрическая винтовая проецировалась в окружность (4 видео)

Цилиндрическая винтовая линия в начертательной геометрии с примером

Цилиндрическая винтовая линия:

Цилиндрическая винтовая линия (гелиса) — это пространственная кривая, представляющая собой траекторию движения точки, равномерно вращающейся вокруг оси и одновременно перемещающейся вдоль этой оси. Высота, на которую поднимается точка по прямой за полный оборот, называется шагом винтовой линии. Если ось винтовой линии перпендикулярна плоскости проекций, то горизонтальная проекция винтовой линии сеть окружность, а фронтальная — синусоида.

На одной поверхности цилиндра может быть несколько винтовых линий с одинаковым шагом. Каждую линию в таком случае называют заходом, а шагом считают расстояние вдоль оси между соседними линиями. Число заходов обозначают

В однозаходной винтовой линии ход равен шагу и между ними различий не делают.

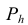
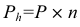
В многозаходной винтовой линии ход связан с шагом и числом заходов выражением (рис. 5.4).

Винтовую линию называют правой, если поднимаясь вверх, точка вращается по часовой стрелке, и левой, если точка вращается против часовой стрелки.

Рекомендую подробно изучить предметы:

Инженерная графика
Начертательная геометрия
Компас
Автокад
Черчение
Проекционное черчение
Аксонометрическое черчение
Строительное черчение
Техническое черчение
Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

Определение и задание поверхностей на чертеже
Классификация поверхностей
Пересечение многогранников плоскостями
Развертка поверхности призмы
Решение задач на тему: перпендикулярности прямой и плоскости
Проекции с числовыми отметками
Перспектива
Построение окружности

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Винтовая линияСкачать

ПОСТРОЕНИЕ ПРОЕКЦИЙ ЦИЛИНДРИЧЕСКОЙ ВИНТОВОЙ ЛИНИИ

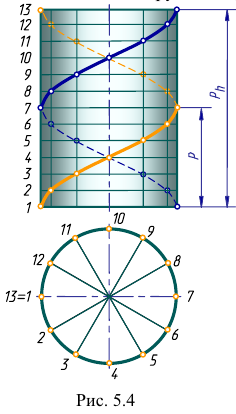
Цилиндрическая винтовая линия может рассматриваться как траектория движения точки, равномерно вращающейся вокруг оси и одновременно перемещающейся в направлении этой оси. В виде цилиндрической винтовой линии остается след острия резца на поверхности равномерно вращающегося цилиндрического стержня при одновременном поступательном движении резца вдоль оси цилиндра. За один оборот цилиндра образуется один виток или оборот винтовой линии. Винтовая линия с двумя витками A_tA₂A₃, оставленная концом резца на цилиндрической заготовке, показана на рис. 7.16. Расстояние Р, проходимое точкой вдоль оси за один оборот, называют шагом винтовой линии, расстояние от точки до оси вращения — радиусом винтовой линии. На одной поверхности цилиндра может быть несколько винтовых линий с одинаковым шагом, например две линии AA₂As и В В₂В> на рис. 7.17. Каждую линию в таком случае называют заходом, а шагом считают расстояние вдоль оси между соседними линиями. Число заходов обозначают п. Перемещение точки вдоль оси за один полный оборот в этом случае называют ходом P_h винтовой линии. С числом заходов п и шагом Р ход P_h связан выражением: P_h = п Р.

Построение на чертеже цилиндрической винтовой линии показано на рис. 7.18. Для построения шаг (фронтальную проекцию О»О»

отрезка оси) и длину окружности цилиндра (горизонтальную проекцию окружности основания диаметром D) разбивают на равное количество частей — п, обычно п = 12, и нумеруют соответствующие образующие. Точка А винтовой линии при повороте на угол 2п/п перемещается вдоль оси на величину Р/п или при п = 12 на 60° и Р/12 соответственно, занимая последовательно положения с проекциями А А,

А‘₂, А«_г, А’₃ за один оборот. Соединив последовательные положения этой точки на фронтальной проекции плавной линией, получают фронтальную проекцию винтовой линии, являющуюся синусоидой. На _{Рис 7 17} рис. 7.18 поверхность цилиндра принята

непрозрачной, поэтому верхняя половина витка показана как невидимая.

Различают правую и левую винтовые линии. Если точка движется по винтовой линии на фронтальной проекции слева-вверх- направо, то такую линию называют правой (см. рис. 7.18). Если движение справа-вверх-налево, то винтовая линия левая.

Развертка винтовой линии — прямая линия показана на рис. 7.18, справа. Угол подъема винтовой линии — а. Значение его определяется по формуле

Угол а характеризует крутизну подъема винтовой линии.

Видео:1 2 4 сопряжение окружностейСкачать

Цилиндрические винтовые линии

По этой ссылке вы найдёте полный курс лекций по математике:

Цилиндрическая винтовая линия представляет собой пространственную кривую линию одинакового уклона. Острие резца, соприкасаясь с поверхностью равномерно вращающегося цилиндрического стержня, оставляет на нем след в виде окружности. Если же при этом сообщить резцу равномерное поступательное движение вдоль оси цилиндра, то на поверхности цилиндра получится цилиндрическая винтовая линия.

На рисунке 218 показано образование винтовой линии на поверхности цилиндра от движения точки А по образующей ЕС и вращательного движения этой образующей. Здесь изображено несколько положений этой образующей: £0С0, £,С„ . ; при этом дуги £,£,, . равны между собой и каждая равна nd/n, где d — диаметр цилиндра, а п — число делений (на рисунке 218 п= 12). Начальное положение точки обозначено через Д), последующее через Л,, Л, и т. д.

Если при перемещении образующей из положения £0С0 в положение £,С, точка займет положение А>, то отрезок £,/1, определит расстояние, которое точка прошла по образующей от своего первоначального положения. При последующем положении образующей (£>С) точка поднимется на высоту Е2А2-2Е[А[ и т. д. Когда образующая сделает полный оборот, точка переместится по ней на расстояние ЕсАа = 12£,/1,. При дальнейшем вращении образующей точка А начнет образовывать второй виток, или оборот винтовой линии, занимая положения А, А и т. д.

На рисунке 219 выполнено построение проекций цилиндрической винтовой линии. Предварительно построены проекции (как это рассматривалось в курсе черчения средней школы) прямого кругового цилиндра. Окружность основания цилиндра (на горизонтальной проекции) и шаг (отрезок h, отложенный по оси цилиндра на фронтальной проекции) разделены на одинаковое число (п) частей; на рисунке 219 взято п- 12. Начальное положение точки А указано проекциями А» и А’ — это точка, отмеченная буквой О’ на окружности.

Так как ось цилиндра направлена перпендикулярно к плоскости ли то горизонтальная проекция винтовой линии сливается с окружностью, представляющей собой горизонтальную проекцию поверхности цилиндра.

Возможно вам будут полезны данные страницы:

Что же касается построения фронтальной проекции винтовой линии, то ход ее построения ясен из рисунка 219 и вытекает из самого образования винтовой линии как траектории точки, совершающей лва движения — равномерное по прямой линии и вместе с тем равномерное вращательное вокруг оси, параллельной этой прямой. Проекция на плоскости, параллельной оси цилиндра, в данном случае фронтальная проекция цилиндрической винтовой линии, подобна синусоиде.

На рисунке 219 фронтальная проекция винтовой линии имеет на передней (видимой) стороне цилиндра подъем слева направо или спуск влево; если же ось цилиндра расположить горизонтально, то подъем винтовой линии идет влево, а спуск — вправо. Это винтовая линия с правым ходом, или правая винтовая линия. Развертка витка цилиндрической винтовой линии показана на рисунке 220. В развернутом виде каждый виток представляет собой отрезок прямой.

Это следует из образования винтовой линии: поскольку окружность основания цилиндра делилась на равное число частей и шаг винтовой линии делился на такое же число равных частей, развертку винтовой линии на протяжении ее шага можно рассматривать как геометрическое место точек, для каждой из которых ордината пропорциональна абсциссе, т. е. у= кх. А это уравнение прямой линии. Касательные к винтовой линии совпадают на развертке с прямой, в которую развертывается виток винтовой линии.

На рисунке 220 при двух шагах

винтовой линии получились два ее отрезка под углом ф, к прямой, представляющей собой развернутую окружность основания цилиндра. Крутизна подъема винтовой линии выражается формулой (2): tg«>i=4> (2) ГШ где h — шаг винтовой линии; d — диаметр цилиндра. Угол ф, называется углом подъема винтовой линии. _

Длина одного оборота «витка» винтовой линии равна L = + (nd)2. При одном и том же d величина угла ф, зависит только от шага винтовой линии; для получения малого угла подъема следует брать малый шаг, и наоборот. Если шаг остается неизменным для цилиндров разного диаметра, то угол подъема получится тем меньше, чем больше будет диаметр цилиндра. Вопросы для самопроверки 1. В чем состоит различие между плоской и пространственной кривыми линиями?

2. Во что проецируется пространственная кривая? 3. Во что проецируется плоская кривая? 4. Во что проецируется касательная к кривой линии? 5. Как определяется длина некоторого участка кривой линии? 6. Что называется касательной к кривой линии? 7. Что называется нормалью в какой-либо точке плоской кривой? 8. Что называется шагом винтовой линии? 9. Что такое правая винтовая линия? 10. Как определяется крутизна подъема винтовой линии? 11. Какие параметры определяют цилиндрическую винтовую линию?

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.