Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.
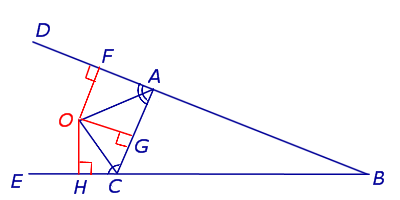
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).
Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:
Следовательно, справедливо равенство
Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства
откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .
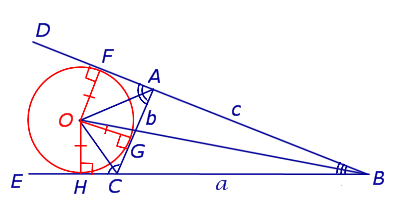
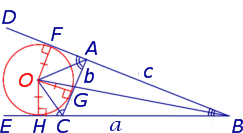
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).
Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.
Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом rb .
Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.
Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство
где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:
где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.
Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле
где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .
Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства
Следовательно, справедливо равенство
что и требовалось доказать.
Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:
Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:
Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности

что и требовалось доказать.
Теорема 5 . Площадь треугольника можно вычислить по формуле
Доказательство . Перемножим формулы
что и требовалось доказать.
Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:
Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим
Преобразуем выражение, стоящее в квадратной скобке:
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

МАТЕМАТИКА
Рассмотрим произвольный треугольник АВС и проведем биссектрису 



Продолжение биссектрисы треугольника, проведенной из одной из вершин, пересекается с биссектрисами внешних углов при двух других вершинах в одной точке.
Поскольку точка 

Эта окружность называется вневписанной окружностью треугольника АВС. Ясно, что любой треугольник имеет три вневписанных окружности. (рис.3).
Положение центра 




Можно сказать, таким образом, что точка 

Принимая во внимание замечание в конце статьи (Точка пересечения продолжения биссектрисы, проведенной из одной из вершин треугольника, с описанной окружностью равноудалена от двух других вершин и центра вписанной окружности), из этого можно сделать еще один вывод:
Точки, в которых вписанная и вневписанная окружности касаются стороны треугольника, симметричны относительно середины этой стороны.
В самом деле, пусть D – точка пересечения продолжения биссектрисы 



Точка касания вневписанной окружности со стороной треугольника обладает еще одним замечательным свойством:
Прямая, проведенная через вершину треугольника и точку, в которой вневписанная окружность касается противоположной стороны, делит периметр треугольника пополам.
Можно убедиться в этом самостоятельно, используя рис. 7.
При решении задач, связанных с нахождением площади треугольника, часто полезной бывает следующая формула. Пусть 
Обозначим эту формулу (1).
Действительно, если две другие стороны данного треугольника равны b и c (рис. 8), то
Замечание. Выпуклый четырехугольник может не иметь вписанной окружности, но он всегда имеет четыре вневписанные окружности.
Любопытно, что для площади S такого четырехугольника имеет место соотношение, похожее на формулу (1).
В самом деле, пусть стороны данного четырехугольника равны последовательно a, b, c и d; p – его полупериметр, 

Пусть 



Применяя к большому треугольнику формулу (1), а к меньшему – формулу , выражающую его площадь через радиус вписанной окружности и полупериметр, получаем:
Обозначим эту формулу (2)
С другой стороны, из подобия треугольников 






Поэтому из полученной пропорции можно найти 
Подставляя это выражение в равенство (2) получим:
Спасибо, что поделились статьей в социальных сетях
Источник: Атанасян Л.С. Геометрия. Дополнительные главы к учебнику 8 кл.: Учебное пособие для учащихся школ и классов с углубленным изучением математики.
Видео:Вневписанная окружностьСкачать

Систематизируем планиметрию
Разделы: Математика
Для подготовки к ЕГЭ (С4) может быть полезна полная систематизация теоретического материала курса планиметрии за 7–9 классы основной школы.
1. Признаки равенства треугольников.
а) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
б) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
в) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
2. В треугольнике против большего угла лежит большая сторона.
3. Сумма углов любого треугольника равна 180 0 .
4. Внешний угол треугольника равен сумме двух других углов треугольника, не смежных с ним.
а, b, с – стороны треугольника
ma, mb, mc – медианы треугольника, la, lb, lc – биссектрисы треугольника,
ha, hb, hc – высоты треугольника, проведенные к соответствующим сторонам
R – радиус описанной окружности; r – радиус вписанной окружности
S – площадь, p – полупериметр
5. Площадь треугольника. S=



6. Соотношения между сторонами и углами в произвольном треугольнике.
Теорема косинусов: Квадрат стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 – 2bc cosA
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов:
=
= 2R
В любом треугольнике сторона равна диаметру описанной окружности, умноженному на синус противолежащего угла. a=2RsinA;
Теорема тангенсов:
=
; a
b;
7. Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
1) Медиана треугольника делит его на два равновеликих (равных по площади) треугольника.
2) Три медианы треугольника пересекаются в одной точке (центр тяжести треугольника), которая делит каждую медиану в отношении 2:1, считая от вершины.
3) Медианы треугольника разбивают треугольник на шесть равновеликих треугольников.
4) Формулы для нахождения длин медиан через длины сторон: ma =
5) Формулы для нахождения сторон треугольника через длины медиан:
a =
8. Биссектриса треугольника – это отрезок луча, выходящего из вершины угла треугольника, делящего этот угол пополам, соединяющий вершину угла с противоположной стороной. Формулы для нахождения длины биссектрисы:
, где a1+b1=c
1) Длина биссектрисы выражается через длины сторон треугольника по формулам:
2) Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам. (рис.1)
=
или
=
3) Биссектриса угла между неравными сторонами треугольника делит угол между радиусом описанной окружности и высотой, проведенными из общей вершины пополам. (рис.2)
4) Точка пересечения продолжения биссектрисы, проведенной из вершины треугольника, с описанной окружностью равноудалена от двух других вершин и центра вписанной окружности. (рис.3)
5) Формулы для вычисления биссектрисы угла; lc =
6) Если биссектрисы треугольника АВС АА1 и СС1 пересекаются в точке Е, то угол АЕС=90° + 
7) Биссектриса внешнего угла треугольника 
9.Высота треугольника – это отрезок луча, выходящего из вершины треугольника, перпендикулярно противолежащей стороне, соединяющий вершину треугольника с ней.
Все высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
Отрезки, соединяющие основания высот остроугольного треугольника, образуют треугольник, биссектрисы которого лежат на этих высотах.
Во всяком непрямоугольном треугольнике произведение расстояний от ортоцентра до концов высоты есть величина постоянная для всех высот данного треугольника.
Если ВВ1 и СС1 – высоты треугольника АВС, О – центр описанной окружности, то отрезок ОА перпендикулярен отрезку В1С1.
Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной данной вершине стороны.
Точки, симметричные ортоцентру треугольника АВС относительно прямых, содержащих его стороны, лежат на описанной окружности треугольника АВС.
Для всякого треугольника зависимость между его высотами ha, hb, hc и радиусом вписанной окружности выражается формулой
10. Подобные треугольники. Признаки подобия треугольников:
а)Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
б)Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы между этими сторонами равны, то треугольники подобны.
в)Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
1) Если треугольники АВС и А1В1С1 подобны, то имеют место следующие равенства:









2) Отношение площадей подобных фигур равно квадрату коэффициента подобия. 
3) Если в остроугольном треугольнике АВС проведены высоты АА1 и СС1, то треугольник А1ВС1 подобен треугольнику АВС с коэффициентом подобия cos B.
4) Теорема Фалеса. Если при пересечении сторон угла параллельными прямыми на одной стороне угла отсекаются равные между собой отрезки, то и на другой стороне угла отсекаются также равные между собой отрезки.
5) Обобщенная теорема Фалеса. При пересечении сторон угла параллельными прямыми на сторонах угла отсекаются пропорциональные отрезки.
6) Теорема Минелая. Если треугольник пересекается секущей, то имеет место следующее соотношение: (рис.6)
7) Теорема Чевы. Если в треугольнике АВС три прямые пересекаются в одной точке, то верно соотношение: (рис.7)
8) Теорема Стюарта. Точка D находится на стороне ВС треугольника АВС.(рис.8)
11. Вписанная и описанная окружности.
1) В любой треугольник можно вписать окружность. Центр вписанной окружности – точка пересечения биссектрис треугольника.
2) Вокруг любого треугольника можно описать окружность. Центр описанной окружности – точка пересечения серединных перпендикуляров.
3) Формула Эйлера (расстояние между центрами вписанной и описанной окружностей)
4) В произвольный треугольник АВС вписана окружность, касающаяся в точках K, L, M сторон АВ, ВС. и СА соответственно. В произвольно выбранной точке N
Имеют место соотношения: 1. BL=p-AC, где р – полупериметр треугольника АВС.
Окружность, касающаяся одной из сторон треугольника, и продолжения двух других его сторон называется вневписанной.
5) Для любого треугольника можно построить три вневписанные окружности.
Радиус вневписанной окружности, касающейся стороны треугольника, имеющей длину a, выражается формулой 
12. Прямоугольный треугольник.
Площадь прямоугольного треугольника можно найти S =
1) 
2) Теорема Пифагора а 2 + b 2 = с 2
3) 
4) 

5)
Медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной окружности.
13. Равносторонний треугольник.
Треугольник, у которого все стороны равны, называется равносторонним. У него все углы равны 60 0 , медианы являются биссектрисами и высотами. Для равностороннего треугольника справедливы следующие формулы:
2. Центральные и вписанные углы. Касательные, хорды, секущие.
Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности.
1. Касательная перпендикулярна к радиусу, проведенному в точку касания.
2. Отрезки касательных к окружности, проведенные из одной точки, равны и образуют равные углы с прямой, проходящей через эту точку и центр окружности.
Прямая, имеющая с окружностью две общие точки, называется секущей.
3. Угол между касательной и секущей, проходящей через точку касания измеряется половиной дуги окружности, лежащей внутри измеряемого угла. (рис.10)
4. Точка касания двух окружностей лежит на линии центров этих окружностей.
5. Общая касательная, проходящая через точку касания двух окружностей, перпендикулярна к линии центров.
6. Общая хорда двух пересекающихся окружностей перпендикулярна к линии центров.
Угол с вершиной в центре окружности называется центральным.
7. Величина центрального угла равна угловой величине дуги, на которую он опирается.
Угол, вершина которого лежит на окружности, а стороны пересекают ее, называется вписанным углом.
8. Величина вписанного угла равна половине угловой величины дуги на которую он опирается.
9. Вписанные углы, опирающиеся на одну и туже дугу, равны.
10. Вписанный угол, опирающийся на диаметр – прямой.
11. Угол с вершиной внутри круга измеряется полу суммой дуг АВ иА 1 В 1 , лежащих, соответственно, внутри данного угла и угла, с ним вертикального.
12. Угол, образованный двумя секущими, проведенными из внешней точки, измеряется полуразностью дуг, лежащих внутри его. (рис.11, 12)
13. Если из точки, лежащей вне окружности, проведены к окружности касательная и секущая, то произведение секущей на ее внешнюю часть равно квадрату касательной. 
14. Для любой секущей, проведенной через данную точку А произведение ее длины на внешнюю часть постоянно. (рис.14)
Отрезок, соединяющий две точки окружности, называется хордой.
15. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
16. Во всяком вписанном четырехугольнике произведения отрезков, на которые разбиваются диагонали точкой их пересечения, равны.
17. Геометрическое место точек из которых данный отрезок виден под постоянным углом, состоит из двух дуг окружностей, симметрично расположенных относительно данного отрезка.
d1, d2 – диагонали,
– угол между диагоналями, S – площадь,
а) Сумма углов выпуклого четырехугольника равна 360 0 .
б) Если четырехугольник можно вписать в окружность, то суммы пар противоположных углов равны 180 о .
в) Если четырехугольник можно описать вокруг окружности, то суммы противоположных сторон равны.
г) Если последовательно соединить середины сторон любого выпуклого четырехугольника, то получится параллелограмм, причем его площадь вдвое меньше площади четырехугольника.
д) Середины двух противоположных сторон любого четырехугольника и середины его диагоналей либо лежат на одной прямой, либо являются вершинами параллелограмма.
е) Теорема Птолемея:Сумма произведений противоположных сторон вписанного четырехугольника равна произведению его диагоналей. ac+bc=d1d2
ж) Диагонали четырехугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
Выпуклый четырехугольник, противоположные стороны которого папарно параллельны, называется параллелограммом.
Противоположные стороны и углы параллелограмма равны. Диагонали параллелограмма точкой пересечения делятся пополам. Диагонали параллелограмма делят его на четыре равновеликих треугольника.
a,b – с тороны,
– острый угол между сторонами
d1, d2 – диагонали,– острый угол между диагоналями
ha, hb – высоты, проведенные к соответствующим сторонам
Параллелограмм, у которого все стороны равны, называется ромбом.
а) Диагонали ромба взаимно перпендикулярны.
б) В любой ромб можно вписать окружность.
, где r – радиус вписанной окружности.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
а) Диагонали прямоугольника равны.
б) Вокруг любого прямоугольника можно описать окружность. d = 2R, где R – радиус описанной окружности.
– стороны, d – диагональ,
– острый угол между диагоналями
Параллелограмм, у которого все стороны равны и все углы равны, называется квадратом.
а) Диагонали квадрата равны и перпендикулярны.
б) В квадрат можно вписать окружность.
, где r – радиус вписанной окружности.
в) Вокруг квадрата можно описать окружность. d = 2R, где R– радиус описанной окружности.
;
Выпуклый четырехугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией.
– основания, d1, d2– диагоналb,
– острый угол между диагоналями,
– средняя линия, h – высота.
а) Если в равнобедренную трапецию можно вписать окружность, то средняя линия равна боковой стороне.
б) В равнобедренной трапеции перпендикуляр, опущенный из вершины меньшего основания на большее делит его на части, большая из которых равна по длине средней линии.
в) Если диагонали равнобедренной трапеции взаимно перпендикулярны, то длина высоты трапеции равна средней линии, а площадь равна квадрату высоты.
г) Если в равнобедренную трапецию можно вписать окружность, то высота трапеции есть среднее геометрическое ее оснований.
д)
, где MN – параллельно основаниям трапеции и делит боковую сторону в отношении m:n.
е)
, где MN– параллельно основаниям и проходит через точку пересечения диагоналей.
ж) Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
з) Если трапеция разделена прямой, параллельной ее основаниям на две равновеликие трапеции, то отрезок этой прямой, заключенной между боковыми сторонами, равен
.
и) Диагонали трапеции делят ее на 4 треугольника, два из которых подобны, а два имеют одинаковую площадь.
к) Если трапеция разделена прямой, параллельной ее основаниям на две подобные трапеции, то отрезок этой прямой, заключенной между боковыми сторонами, равен
4. Правильные многоугольники
Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны.
а) Соотношения между стороной
, радиусом вписанной
, и радиусом описанной окружности
:
;
;
б) Периметр и площадь правильного n– угольника:
;
в) Сумма угловправильного n-угольника равна 180(n-2).
г) Угол правильного n-угольника равен
.
5. Длина окружности, площадь круга.
;
📽️ Видео
Вневписанная окружностьСкачать
Построить описанную окружность (Задача 1)Скачать
Геометрия. 8 класс. Урок 8 "Биссектриса как ГМТ. Вписанная и вневписанная окружности треугольника"Скачать
Вневписанная окружность | Теоремы об окружностях - 3Скачать
Вписанная и описанная окружность - от bezbotvyСкачать
[12] Площадь через радиус вневписанной окружности. Теорема о трилистнике, трезубец, Теорема МансионаСкачать
Задача про две вневписанные окружности | ЕГЭ. Задание 16. Математика | Борис Трушин |Скачать
ЕГЭ 2021 Математика. Метод площадей. Теорема Чевы. Вневписанная окружностьСкачать
Вневписанная окружность. Практика. Задача из Ященко | Профильная математика в онлайн - школе СОТКАСкачать
Это будет на ЕГЭ 2020 по математике. Вписанная и вневписанная окружности.Скачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Вписанная и описанная около равнобедренного треугольника, окружностьСкачать
Вневписанные окружности, с4 егэСкачать
Вневписанная окружность.Теорема Птоломея.Скачать
8 класс, 38 урок, Вписанная окружностьСкачать
ЕГЭ-2020. №16. Вневписанная окружность🚀 Ортоцентр. Теорема Карно, Бланшета, Чевы, Менелая🔥Скачать
Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать
Строим вписанную в данный треугольник окружность (Задача 2).Скачать

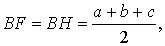

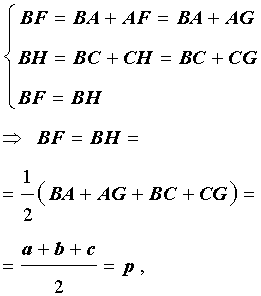
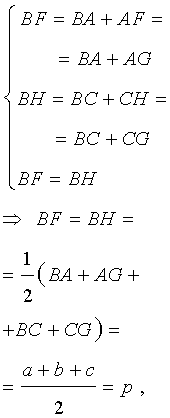
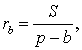
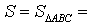

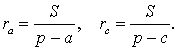
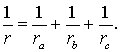
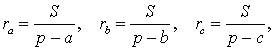
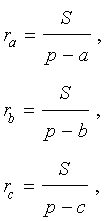
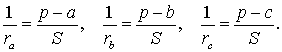
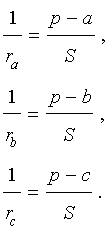
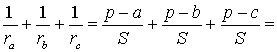
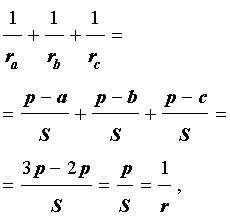
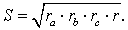
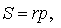
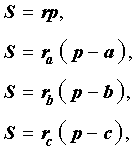
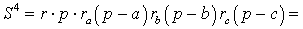
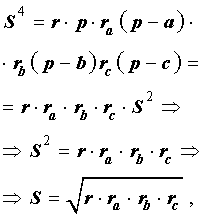
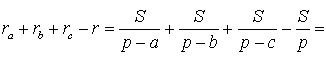
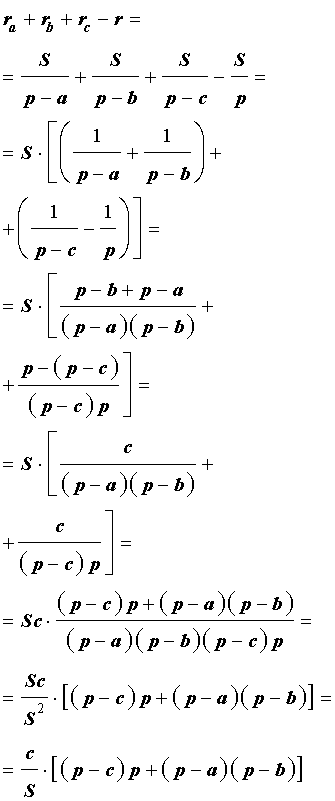
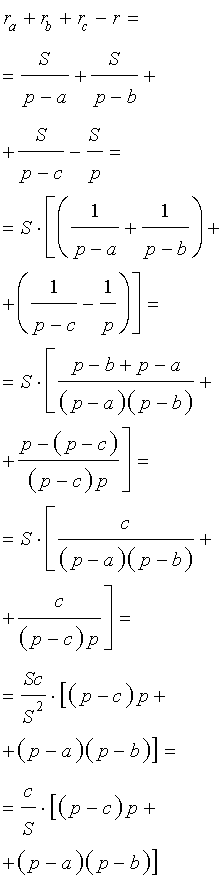















 =
=  = 2R
= 2R =
=  ; a
; a  b;
b;

 , где a1+b1=c
, где a1+b1=c

 =
=  или
или  =
=






























 – угол между диагоналями, S – площадь,
– угол между диагоналями, S – площадь, 
 – острый угол между сторонами
– острый угол между сторонами 

 , где r – радиус вписанной окружности.
, где r – радиус вписанной окружности. – стороны, d – диагональ,
– стороны, d – диагональ, 
 , где r – радиус вписанной окружности.
, где r – радиус вписанной окружности. ;
;
 – средняя линия, h – высота.
– средняя линия, h – высота.

 , где MN – параллельно основаниям трапеции и делит боковую сторону в отношении m:n.
, где MN – параллельно основаниям трапеции и делит боковую сторону в отношении m:n. , где MN– параллельно основаниям и проходит через точку пересечения диагоналей.
, где MN– параллельно основаниям и проходит через точку пересечения диагоналей. .
.
 , радиусом вписанной
, радиусом вписанной  , и радиусом описанной окружности
, и радиусом описанной окружности  :
: ;
;  ;
; 
 ;
; 
 .
.
 ;
; 




![[12] Площадь через радиус вневписанной окружности. Теорема о трилистнике, трезубец, Теорема Мансиона](https://i.ytimg.com/vi/lQN1nl99Yr0/0.jpg)