Для любого числа k и любого вектора a (8 видео)

Коллинеарность векторов, условия коллинеарности векторов.

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).

рис. 1

Содержание

Условия коллинеарности векторов
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Примеры задач на коллинеарность векторов в пространстве
Урок «Умножение вектора на число»
Для любых векторов m, p, q и любого числа k верно
Ваш ответ
решение вопроса
Похожие вопросы
💡 Видео

Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Условия коллинеарности векторов

Два вектора будут коллинеарны при выполнении любого из этих условий:

Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что

N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.

N.B. Условие 3 применимо только для трехмерных (пространственных) задач.

Доказательство третего условия коллинеарности

Пусть есть два коллинеарные вектора a = < a_x ; a_y ; a_z > и b = < na_x ; na_y ; na_z >. Найдем их векторное произведение

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Примеры задач на коллинеарность векторов

Примеры задач на коллинеарность векторов на плоскости

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:

a_x	=	a_y	.
b_x		b_y

Вектора a и b коллинеарны т.к.	1	=	2	.
	4		8

Вектора a и с не коллинеарны т.к.	1	≠	2	.
	5		9

Вектора с и b не коллинеарны т.к.	5	≠	9	.
	4		8

Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

n =	b_y	=	6	= 2
	a_y		3

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности

a_x	=	a_y	.
b_x		b_y

3	=	2	.
9		n

Решим это уравнение:

n =	2 · 9	= 6
	3

Ответ: вектора a и b коллинеарны при n = 6.

Примеры задач на коллинеарность векторов в пространстве

Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:

a_x	=	a_y	=	a_z	.
b_x		b_y		b_z

Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12

Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12

Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12

Для этого найдем ненулевой компонент вектора a в данном случае это a_y . Если вектора колинеарны то

n =	b_y	=	6	= 2
	a_y		3

Найдем значение n a :

Так как b = n a , то вектора a и b коллинеарны.

a_x	=	a_y	=	a_z	.
b_x		b_y		b_z

3	=	2	=	m
9	=	n	=	12

Из этого соотношения получим два уравнения:

3	=	2
9	=	n

3	=	m
9	=	12

Решим эти уравнения:

n =	2 · 9	= 6
	3

m =	3 · 12	= 4
	9

Ответ: вектора a и b коллинеарны при n = 6 и m = 4.

Видео:Умножение вектора на число. 9 класс.Скачать

Урок «Умножение вектора на число»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна модуль |k| умноженный на модуль |а|, причем векторы а и b сонаправлены, если k положительно и противоположно направлены, если k отрицательно.

Произведение вектора а на число k обозначается так: ka.

Для любого числа k и любого вектора а векторы а и ka коллинеарны.

Произведением нулевого вектора на любое число считается нулевой вектор.

Произведение любого вектора на число нуль есть нулевой вектор.

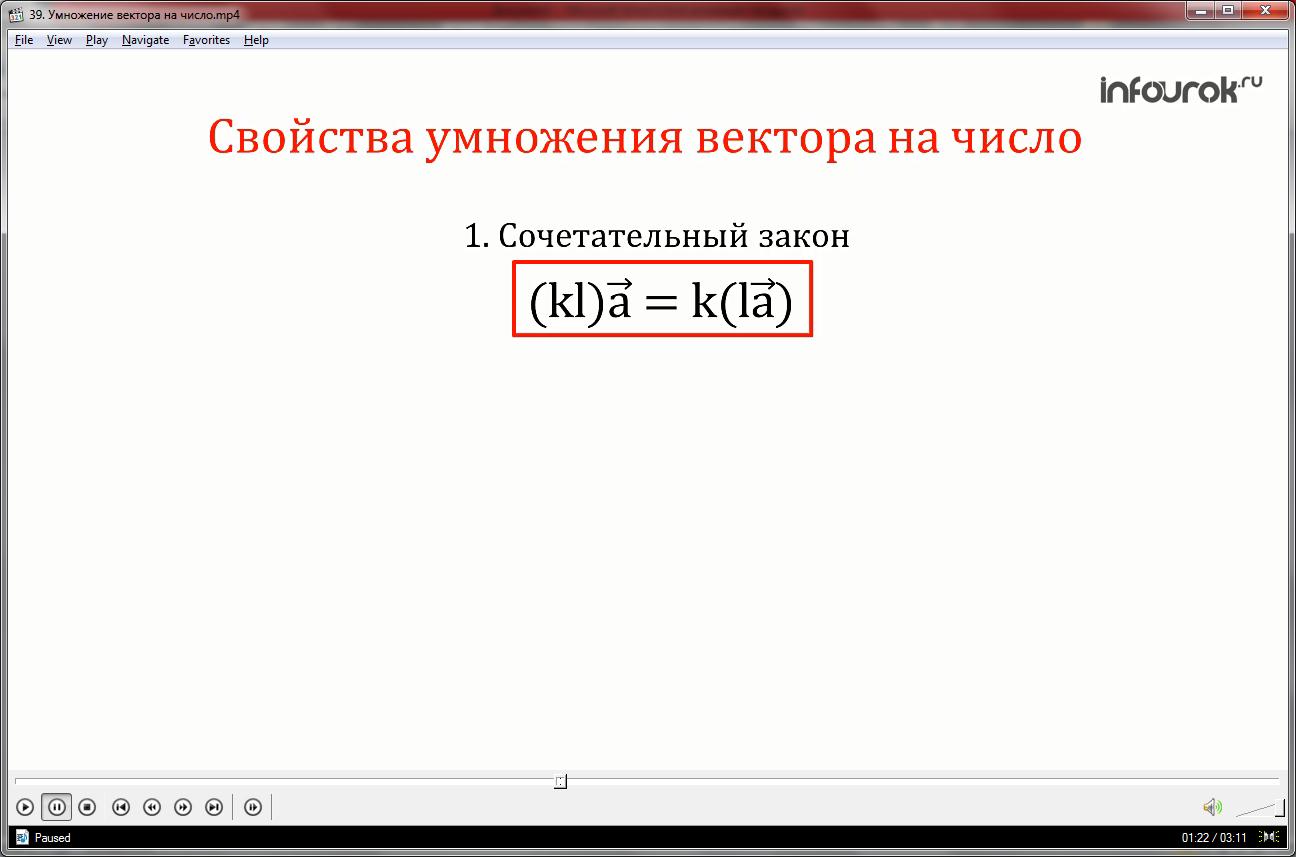
Рассмотрим основные свойства умножения вектора на число. Для любых векторов а,b и любых чисел k и l справедливы равенства:

Первое. Произведение k и l, умноженное на вектор а, равно произведению k на вектор lа. Это свойство известно как сочетательный закон. На рисунке, на примере показано это свойство.

Второе свойство, первый распределительный закон. Произведение числа k на сумму векторов а и b равно сумме произведений этого числа на векторы а и b.

На рисунке, на примере показано это свойство.

Третье свойство, второй распределительный закон. Произведение суммы чисел k и l на вектор равно сумме произведений чисел k и l на вектор а.

На рисунке, на примере показано это свойство.

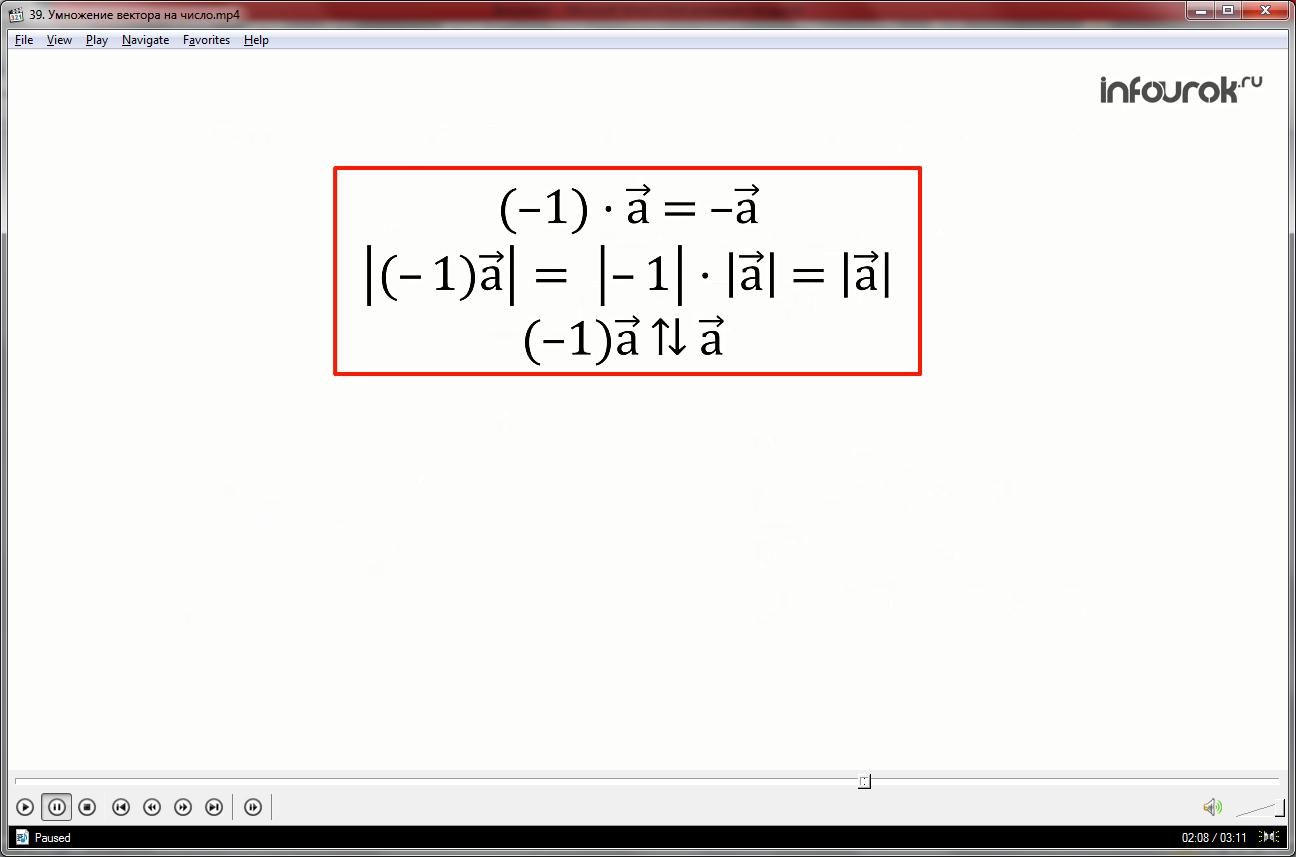
Стоит отметить, что произведение числа -1 на любой вектор дает вектор противоположный данному.

Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.

Для векторов в пространстве, как и в планиметрии, выполняется следующее условие:

Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b равен произведению числа k на вектор а.