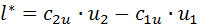Для чего нужны треугольники скоростей (5 видео)

Для чего нужны треугольники скоростей

Содержание

Главное меню
Судовые двигатели
Треугольники скоростей осевых компрессоров
Тема №2: Понятие ступени осевой турбины
📺 Видео

Главное меню

Судовые двигатели

При использовании кинетической энергии пара при умеренных окружных скоростях применяют турбины со ступенями скорости. Для определения скоростей пара пользуются методом построения треугольников.

Процесс течения пара в чисто активной (? = 0) турбине с двумя ступенями скорости с учетом потерь показан на рис. 81, а. Превращение потенциальной энергии пара в кинетическую происходит так же, как в одноступенчатой активной турбине, только в одном ряде сопел. Действительная абсолютная скорость пара на выходе из сопел с ₁ = 44,8? ? h _а и направлена под углом ? ₁ к направлению окружной скорости. Геометрическим вычитанием находят относительную скорость входа пара на рабочие лопатки первого ряда w ₁ направленную под углом ? ₁ .

Относительная скорость пара на выходе из рабочих лопаток первого ряда ? ₂ = ? ₁ ? ₁ (? ₁ — скоростной коэффициент первого ряда рабочих лопаток) и направлена под углом ? ₂ . Геометрическим сложением находят абсолютную скорость с ₂ выхода пара с лопаток первого ряда, направленную под углом ? ₂ :

Пар входит на направляющие лопатки ступени со скоростью с ₂ , но из-за вредных сопротивлений она уменьшается до c ₁ ’ =? _н с ₂ (? _н — скоростной коэффициент на направляющих лопатках). Скорость с ₁ ‘ направлена под углом ? ₁ ’. Геометрическим вычитанием находят относительную скорость пара w ₁ ’, направленную под углом ? ₁ ’:

Аналогично, как и для лопаток первого ряда, определяют

где w ₂ ’ и с ₂ ’ — относительная и абсолютная скорости на выходе из лопаток второго ряда, направленные соответственно под углами ? ₂ ’ и ? ₂ ’; ? ₂ — скоростной коэффициент рабочих лопаток второго ряда.

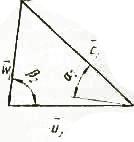
Треугольники скоростей удобно совмещать к одному полюсу для каждой ступени или для всех ступеней (рис. 81, б ). Из треугольников скоростей следует:

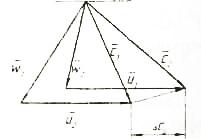
Для определения окружного коэффициента полезного действия предполагается, что процесс течения пара в турбине совершается без потерь (? = ? = 1). Выходная потеря будет наименьшей (? ₂ ’ = 90°). и лопатки турбины имеют симметричный профиль (? ₁ = ? ₂ при ? = 0). Треугольники скоростей такой ступени имеют вид, приведенный на рис. 82.

Из треугольника АОВ имеем

Из выражения следует, что, как и у одноступенчатой турбины, в турбине со ступенями скорости окружной к. п. д. зависит от отношения скоростей и/с ₁ . При двух значениях и/с ₁ = 0 и и/с ₁ =cos ? ₁ /z окружной к. п. д. будет равен нулю. Взяв первую производную из выражения (60) по и/с ₁ и приравняв ее нулю, получают максимальное значение окружного к. п. д. такое же, как и для одноступенчатых турбин, ? _и _m _ах = cos 2 ? ₁ при значении и/с ₁ = cos ? ₁ /2 z . Отсюда видно, что при одинаковых адиабатных теплоперепадах многовенечная турбина со ступенями скорости будет иметь окружную скорость в z раз меньше, чем одновенечная. Иначе, при одинаковой окружной скорости турбина, имеющая z ступеней скорости, может срабатывать адиабатный теплоперепад в z раз больше, чем одновенечная ступень.

С учетом потерь наивыгоднейшее отношение и/с ₁ находится в пределах: для двухвенечных колес 0,20—0,25 и трехвенечных 0,10—0,18. Наивыгоднейшее значение и/с ₁ определяется таким же образом, как и для одноступенчатой турбины путем пробных расчетов, построением треугольников скоростей, вычислением ? ₀ _i = ? _и — ? _тв и построением кривой ? ₀ _i == ? (и/с ₁ ).

Окружной к. п. д. для многовенечных ступеней ? _u можно определить по формуле, аналогичной (33) и распространенной на несколько ступеней скорости. Измерив по треугольникам каждого венца значения ( с _{1 и} ± с _{2 и} ) и сложив их, получают окружной теплоперепад

Для построения процесса расширения на s — i -диаграмме необходимо построить треугольники скоростей и определить потери трения в каналах. Для двухвенечной активной ступени (? = 0) потери определяются по следующим формулам:

Откладывая эти потери последовательно от точки А ₁ _t вверх (рис. 83) на s— i -диаграмме, получают теплоперепад

h _u = i ₀ – i _E ₁ ,

использованный на окружности турбинного колеса. Окружной к. п. д.

Далее определяют сумму внутренних потерь ? q _i = q _тв + q _x и, откладывая их от точки Е ₁ вверх, находят на изобаре точку F ₁ , которая соответствует состоянию пара на выходе из двухвенечной ступени. Использованный внутренний теплоперепад составляет

Одним из основных мероприятий, ведущих к повышению экономичности многовенечных ступеней, является допуск небольшой реакции на рабочие и направляющие венцы. Кроме того, реактивность обеспечивает плавное изменение высот лопаток проточной части ступени.

Степени реакции в венцах

где h _л1 , h _н , h _л2 —адиабатные теплоперепады на первом рабочем, направляющем и втором рабочем венцах;

h _а — общий адиабатный теплоперепад.

Так как h _a = h _с + h _л1 + h _н + h _л2 , то адиабатный теплоперепад, приходящийся на сопловой аппарат,

При наличии реакций в венцах скорости пара на выходе из соответствующих венцов определяют по формулам:

Порядок построения процесса (рис. 84) следующий.

1. По начальным и конечным параметрам пара определяют на диаграмме располагаемый теплоперепад h _а = i ₀ — i ₁ _t кдж/кг.

3. От точки А ₀ откладывают вниз теплоперепад h _с и на пересечение с адиабатой A ₀ A ₁ _t получают точку а. Изобара р 1 , проходящая через точку а, соответствует давлению пара за соплом.

4. Определяют потери в сопле q _с и откладывают ее от точки а вверх, в результате получают точку А ₁ , характеризующую состояние пара на выходе из сопла; линия А ₀ А ₁ есть процесс расширения в сопле.

5. Находят теплоперепад на лопатках первого ряда h _л1 =? _л1 h _а и откладывают его от точки А ₁ вниз. Изобара р», проходящая через точку b, соответствует давлению пара за первым рабочим венцом.

6. Строят треугольники скоростей для первого рабочего венца и по относительной скорости w ₂ , определяемой по формуле (64), находят по формуле (65) потери q _л1 . Откладывая эти потери от точки b вверх, получают на изобаре р» точку В ₁ , которая характеризует состояние пара после первого ряда рабочих лопаток.

7. Аналогичным образом путем построения треугольников скоростей находят соответствующие скорости. Отложив последовательно теплоперепады h _н и h _л2 и потери q _н и q _л2 , получают точку D ₁ , определяющую состояние пара после рабочих лопаток второго ряда.

[1] Определяют выходные потери q _в и, отложив ее от точки D ₁ вверх, получают точку Е ₁ определяющую состояние пара на выходе из ступени. Разность начальной энтальпии i ₀ и i _E ₁ соответствует окружному теплоперепаду в ступени h _и = i ₀ — i _E ₁ кдж/кг (кал/кг).

С повышением степени реакции, окружной к. п. д. повышается. Графическая зависимость з _и = ц ( u / c ₁ ) для различных степеней реакции в венцах двухвенечной ступени показана на рис. 85. На кривых указаны степени реакции (в процентах) для рабочих и направляющих лопаток.

Высота сопел и лопаток определяется по уравнению сплошности для различных частей проточной части, при этом:

Деля по частям последние три уравнения на первое и принимая во внимание зависимости, а также считая одинаковыми коэффициенты сужения . ₁ ?? _н ?? ₂ для всех профильных решеток проточной части ступени, получаем

Для расчета чисто активных ступеней (? = 0) можно изменением удельных объемов пренебречь и приближенно определить высоты по выражениям

Видео:Турбинная ступень. Треугольники скоростейСкачать

Треугольники скоростей осевых компрессоров

В соответствии с основным уравнением турбомашин (уравнением Леонарда Эйлера) работа, переданная лопатками рабочего колеса единице протекающей массы, определяется выражением

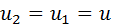
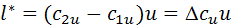
или для осевых машин с движением по цилиндрическим поверхностям тока, когда , как

Таким образом, энергообмен в рабочем колесе определяется кинематикой потока, а именно величиной окружной скорости решетки и изменением окружной составляющей абсолютной скорости потока от входа в колесо до выхода из него. Поэтому ясное представление о форме движения в рабочем колесе чрезвычайно важно для понимания основных особенностей работы турбомашин, в частности компрессоров.

Форма течения в области рабочего колеса определяется скоростями абсолютного движения (обозначаемыми в дальнейшем с), построенными в неподвижной системе координат (системе, связанной с корпусом машины), переносного движения (u) — движения лопаток рабочего колеса и относительного движения (w), то есть движения среды относительно движущихся с окружной скоростью лопаток рабочего колеса. Скорость относительного движения — это скорость среды в системе координат, связанной с вращающимися лопатками рабочего колеса.

Основной связью, определяющей соотношения между абсолютными, переносными и относительными скоростями, является условие сложения векторов 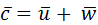, утверждающее, что вектор абсолютной скорости является суммой векторов скоростей переносной и относительной. Графическое изображение условия называется треугольником скоростей, который может быть построен как для входа в рабочее колесо, то есть для течения перед рабочим колесом, так и для выхода из рабочего колеса.

Совмещенные треугольники скоростей для входа и выхода называются иногда планами скоростей, они характеризуют кинематику потока в рабочем колесе, в конечном счете определяющую и величину переданной работы.

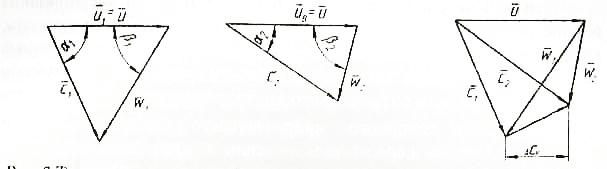
В современной практике проектирования и расчета турбомашин в основном используются два метода совмещения треугольников при построении планов скоростей. В компрессоро- и турбостроении план скоростей обычно строится при совмещении началам векторов абсолютных и относительных скоростей для треугольников входа и выхода (рис. 1).

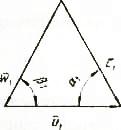
Рис.1. Треугольники скоростей при совмещении начала их векторов

В вентиляторостроении при анализе режимов работы осевых ступеней с течением по цилиндрическим поверхностям тока (когда 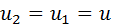) планы скоростей строят совмещением векторов окружных скоростей (рис.2).

Очевидно, оба момента построения планов скоростей допустимы и поэтому необходимо всегда уметь перейти от одной формы плана скоростей к другой.

Вполне естественно, что треугольники скоростей, т.е. план скоростей, отражающих картину течения, определяются как неподвижными, так и подвижными лопатками и, прежде всего, их геометрической формой.

Рис. 2 Треугольники скоростей при совмещении векторов окружных скоростей

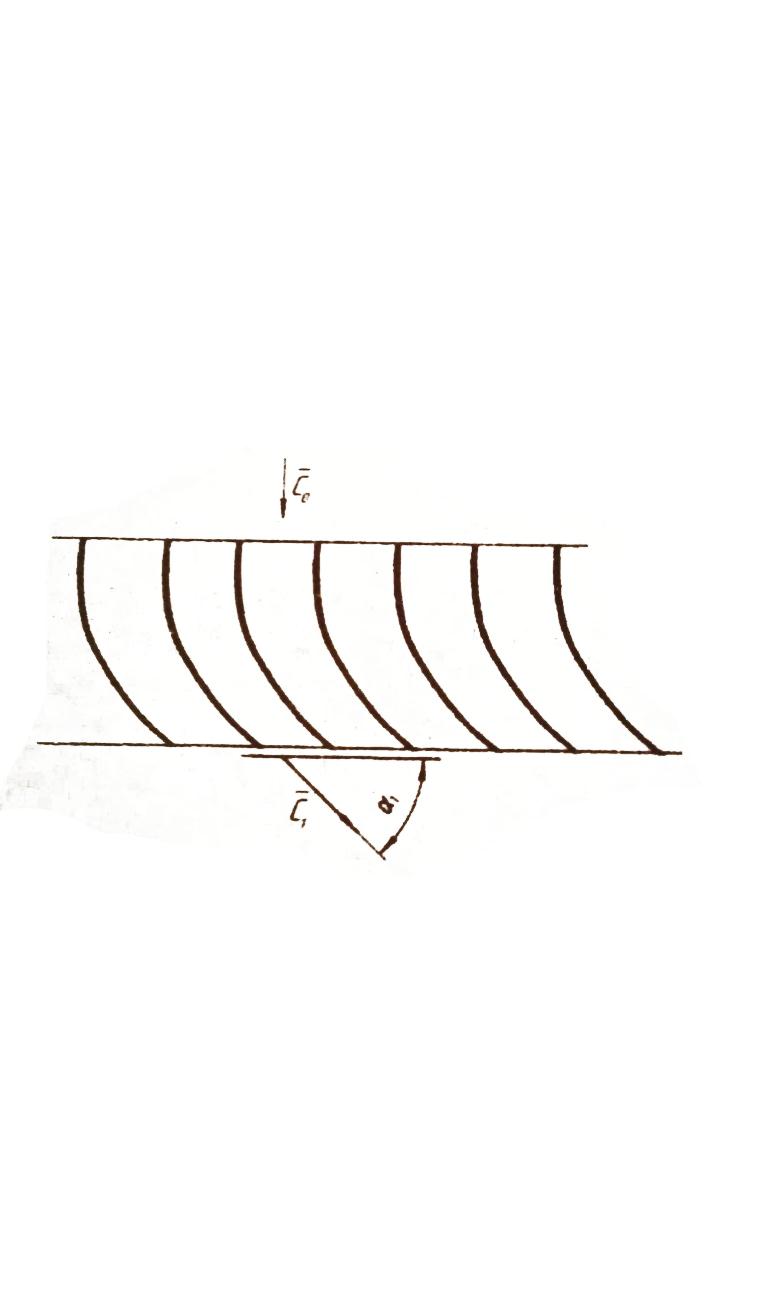
Действительно, проследим, за потоком от входа в ступень осевого компрессора до выхода из него. Предположим, что перед решеткой входного направляющего аппарата среда движется в осевом направлении, то есть вдоль оси машины. Решетка направляющего аппарата в этом случае разместится поперек движущегося потока. Если мы будем рассматривать течение на какой-либо цилиндрической поверхности, соосной с осью ступени, то, развернув такую поверхность на плоскость, получим картину, изображенную на рис. 3.

Рис. 3 Схема входа потока в направляющий аппарат

Рис.4. Схема обеспечения заданного

направления потока на выходе из решетки пластин

Так как направление векторов с₀ определяется особенностями течения где-то впереди рассматриваемой ступени и является заданным, то конструктор, проектируя ступень и стремясь уменьшить потери при обтекании лопаток, очевидно, должен придать входным элементам лопаток неподвижной решетки направление, примерно соответствующее вектору абсолютной скорости с₀, набегающего на лопатки потока.

Входной направляющий аппарат (ВНА) ставится для придания вполне определенного направления потоку перед рабочим колесом, выбираемого при проектировании наиболее выгодной для заданных условий ступени. Если направление скорости перед рабочим колесом задано вектором с₁,то очевидно, что это направление должны придать потоку лопатки входного направляющего аппарата. Вполне естественно, что в первом приближении направление потока на выходе из решетки определится направлением выходных кромок лопаток, что становится совершенно очевидным при предельном переходе к решетке из бесконечно тонких пластин, очень близко расположенных друг к другу (рис. 4).

В реальных решетках действительное направление скорости отличается от направления выходных кромок лопаток втем большей степени, чем больше расстояние между лопатками. На направление скорости выхода влияют и другие геометрические характеристики решетки, а также режимы обтекания (числа М и Re, углы набегания потока на лопатки и т.д.).

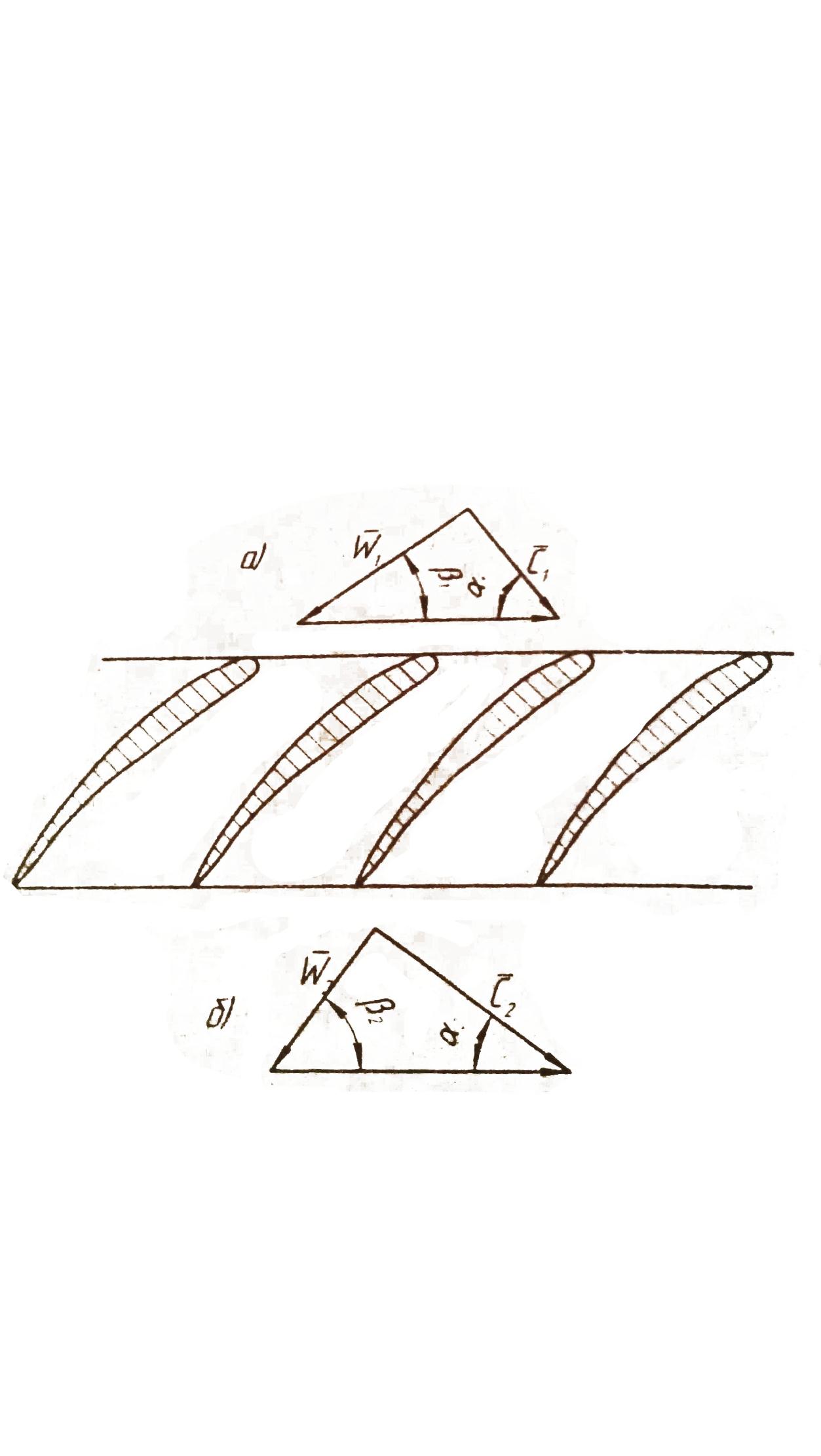
Рис. 5. Треугольники на входе и выходе рабочего колеса осевого компрессора

Если перед рабочим колесом течение определяется вектором с₁ (скоростью выхода среды из входного направляющего аппарата), то на перемещающиеся лопатки рабочего колеса поток набегает со скоростью и, следовательно, треугольник скоростей перед лопатками рабочего колеса имеет вид, изображенный на рис. 5а.

Профилируя лопатки рабочего колеса, конструктор, стремясь уменьшить потери при набегании потока на лопатки, придает их входным кромкам направление, совпадающее с направлением набегающего потока, то есть с направлением скорости w₁.

Выбрав кривизну лопаток (то есть форму и направление выходных кромок), конструктор определяет и направление относительной скорости на выходе из рабочего колеса, а следовательно, и форму треугольника скоростей на выходе из рабочего колеса (рис. 5б). Совмещение треугольников скоростей рабочего колеса даёт совмещенный план скоростей при неравенстве расходных составляющих скоростей с₁_z 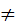с₂_zперед и за рабочим колесом. При равенстве расходных составляющих скоростей с_1z = с_2z построение треугольников скоростей упрощается (рис.7).

Видео:Как рисовать треугольники скоростей на экзамене. Паровые турбиныСкачать

Тема №2: Понятие ступени осевой турбины

При создании своих турбин Лаваль и Парсонс шли разными путями.

Отличительной особенностью турбин Лаваля было то, что расширение пара происходило только в соплах. Преобразование кинетической энергии струй пара на выходе из сопел в механическую энергию вращения ротора осуществлялось без дальнейшего расширения пара, а только за счет изменения направления потока в каналах рабочих лопаток (лопаток, закрепленных на колесе). Турбины, работающие по такому принципу получили название активных или импульсных.

Паровая турбина, предложенная Парсонсом существенно отличалась от турбины Лаваля.

Расширение пара в ней происходило не в одной сопловой группе, а в ряде следующих друг за другом ступеней, каждая из которых состояла из неподвижных закрепленных в корпусе сопловых и рабочих лопаток, расположенных на роторе и вращающихся вместе с ним.

В каждой ступени срабатывался таким образом перепад давления, составляющий лишь часть полного перепада на турбину.

Именно это позволило работать с меньшими скоростями потока и частотами вращения ротора.

Кроме того, расширение пара в турбине Парсонса происходило не только в сопловой, но и в рабочей решетках. Поэтому рабочее колесо передавало усилие на ротор не только вследствие изменения направления потока пара, но и благодаря ускорению пара в каналах рабочего колеса, т.е. вследствие возникновения реактивного усилия.

Турбины такого типа (расширение пара в равной степени происходит в сопловом аппарате и рабочем колесе) получили название реактивных.

В настоящее время разница между активными и реактивными турбинами стерлась – и те и другие делаются многоступенчатыми. Однако конструктивные отличия сохраняются (об этом мы поговорим позже).

Как уже должно стать понятным, процесс расширения пара в турбине происходит в ряде последовательно расположенных друг за другом ступеней. Таким образом, ступень является важнейшим и основным элементом турбомашины.

Задачей инженера, проектирующего турбину, является такая организация потока в каждой отдельной ступени, при которой потери будут наименьшими, и тем самым обеспечить высокий КПД турбины в целом.

Это невозможно сделать без глубоких знаний процессов, происходящих в ступени турбомашины.

Изучением этих процессов мы и займемся в первой части нашего курса.

Преобразование энергии в турбинной ступени

Разберемся для начала с принципом работы турбинной ступени и процессами преобразования энергии, которые в ней протекают.

Турбинная ступень образуется из неподвижной (сопловой) и вращающейся (рабочей) лопаточных решеток, расположенных друг за другом по ходу движения рабочего тела.

В каждой решетке лопатки одинаковы, установлены под одним углом и находятся на одинаковом расстоянии друг от друга.

Далее мы будем рассматривать ступени только осевых турбомашин, которые получили наибольшее распространение при относительно больших мощностях агрегатов.

На рис. 2.1 снизу представлена схема осевой турбинной ступени.

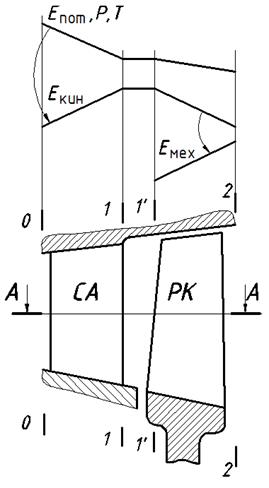
У турбинной ступени принято различать следующие сечения ступени: 0–0 –перед СА; 1–1 – за СА; 1’–1’ – перед рабочим колесом, 2–2 – за рабочим колесом или за ступенью. Параметры потока (давления, температуры, скорости и др.) в этих сечениях отличаются индексами, соответствующими номеру сечения.

Каждый венец лопаток в ступени выполняет свои функции.

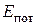
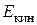
В сопловом аппарате (СА) потенциальная энергия рабочего тела преобразуется в кинетическую энергию потока . Другими словами в сопловом аппарате увеличивается скорость потока за счет снижения давления и температуры рабочего тела.

В рабочем колесе ступени за счет обмена импульсами движения между потоком рабочего тела и лопаточным аппаратом рабочего колеса накопленная кинетическая энергия потока преобразуется в механическую энергию вращения ротора 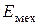. Кроме того, в РК продолжается преобразование потенциальной энергии рабочего тела в кинетическую энергию потока. Естественно, что оба эти процесс происходят одновременно.

Как видим, принцип преобразования энергии в турбинной ступени довольно прост. Вместе с тем, при более детальном рассмотрении процессов, протекающих в ступени, возникают некоторые нюансы, связанные с тем, что один венец лопаток неподвижен (СА), а другой вращается вместе с ротором (РК).

Кинематика турбинной ступени

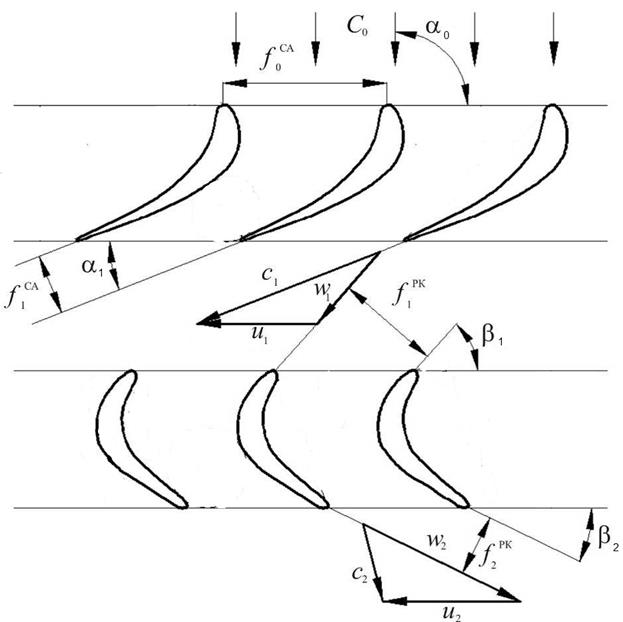
Если мысленно рассечь лопатки ступени цилиндрической поверхностью А–А (рис. 2.1) и развернуть на плоскость, то сечения лопаток представляются в виде рядов профилей, образующих решетки профилей соплового аппарата и рабочего колеса (рис. 2.2).

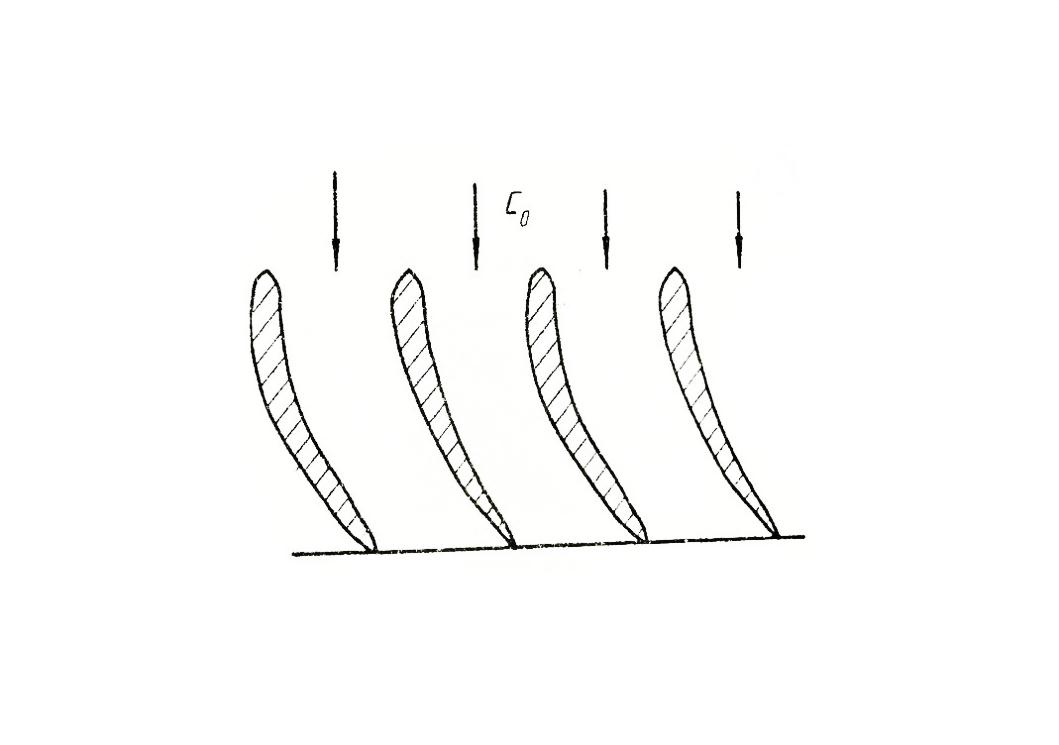
Подвод рабочего тела к сопловому аппарату, как правило, выполняется осевым, т.е. поточный угол a₀, под которым направлена скорость С₀, равен 90°. Скорость С ₀ – это скорость рабочего тела на входе в сопловой аппарат ступени.

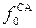
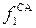
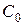
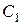
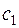
Изогнутые межлопаточные каналы СА формируют сужающийся (конфузорный) канал ( > ) и тем самым обеспечивают увеличение скорости от до . Само сужение канала возможно только при условии, что a₁0. Поэтому этом поток в СА не только ускоряется, но и разворачивается. Таким образом на выходе из соплового аппарата скорость потока будет равна и направлена под углом a₁.

Скорость выхода пара из сопловой решетки наглядно изображается вектором С ₁. Однако на профили движущейся рабочей решетки пар будет поступать не под углом a₁ а под другим углом, так как решетка вращается с окружной скоростью U. В результате пар натекает на рабочие лопатки под углом b₁ с относительной скоростью W₁, равной разности векторов скоростей С ₁ и U.

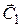
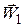
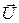
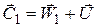
Здесь используется правило теоретической механики, согласно которому абсолютная скорость ( ) равна сумме относительной ( ) и переносной скоростей ( ):

Построенные таким образом векторы образуют треугольник, часто называемый входным треугольником скоростей.

Для безударного обтекания потоком лопаток и во избежание срывов потока передние кромки РЛ необходимо ориентировать по направлению скорости .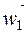

Пар, поступив в каналы рабочей решетки, взаимодействует с ее профилями, создавая окружную силу, вращающую диск.

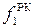
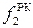
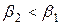
Каналы рабочего колеса также выполняются сужающимися – это позволяет реализовать дальнейшее преобразование потенциальной энергии рабочего тела в кинетическую энергию потока. Сужения канала можно добиться только при условии, что > , что возможно если задние кромки необходимо направить таким образом, чтобы .

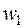
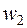
Таким образом, в каналах РК поток рабочего тела разворачивается и ускоряется от скорости на входе до скорости на выходе из РК.

Покидает пар рабочую решетку с относительной скоростью W ₂, под углом выхода b₂.

Рис. 2.2. Плоские решетки профилей лопаточных венцов ступени: схема течения продуктов сгорания в ступени турбины и основные геометрические характеристики профилей лопаток:

, , , − площадь проходного сечения на входе и выходе межлопаточного канала в СА и РК соответственно

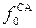
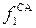
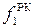
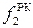
Абсолютная скорость выхода пара С₂ представляет собой сумму векторов W ₂ и U. Она будет составлять угол a₂ с плоскостью вращения. Полученный треугольник векторов скоростей называют выходным треугольником скоростей.

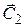
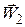
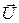
Здесь также используется правило теоретической механики, согласно которому абсолютная скорость ( ) равна сумме относительной ( ) и переносной скоростей ( ):

Полученные таким образом треугольники скоростей обычно совмещают и кратко называют треугольниками скоростей (рис. 2.3). Они позволяют лучше понять, каким образом в ступени внутренняя энергия пара превращается в работу.

Рис. 2.3. План (треугольники) скоростей осевой турбинной ступени

Таким образом, поток рабочего тела в турбинной ступени характеризуется рядом кинематических характеристик:

– абсолютная скорость потока на входе в ступень (СА);

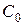
a₀ – угол, с которым поток входит в ступень (СА) в абсолютном движении;

– абсолютная скорость потока на выходе из СА;

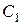
a₁ – угол выхода потока из СА в абсолютном движении;

– относительная скорость потока на входе в РК;

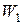
b₁ – угол входа потока в РК в относительном движении;

– относительная скорость потока на выходе из РК;

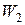
b₂ – угол выхода потока из РК в относительном движении;

– абсолютная скорость потока на выходе из ступени;

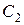
a₂ – угол выхода потока из ступени в абсолютном движении;

— окружная скорость рабочего колеса. Здесь — диаметр, котором определяется скорость, — частота вращения ротора.

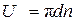
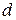
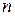
Следует подчеркнуть, что абсолютные кинематические параметры потока определяются относительно неподвижного соплового аппарата.

Если те же самые скорости измерить относительно вращающегося рабочего колеса, то мы будем иметь относительные кинематические параметры.

Для треугольников турбинной ступени существуют соотношения, которые не могут быть нарушены, т.к. в противном случае ступень перестает выполнять свои функции:

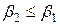
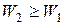
Помимо приведенных выше кинематических параметров в теории турбомашин очень широкое распространение нашли проекции скоростей.

Всего выделяют два вида проекции: окружные (на ось u) и осевые (на ось a), см. рис. 2.3.

Окружные проекции используются при вычислениях мощностных показателей ступени (см. ниже). Приведем основные уравнения для их вычисления:

;

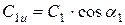
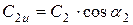
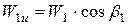
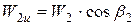
При этом окружные проекции обладают следующими свойствами:

;

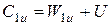
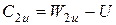
Осевые проекции характеризуют расход рабочего тела через сечения ступени. Приведем основные уравнения для их вычисления:

;

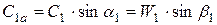
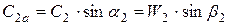
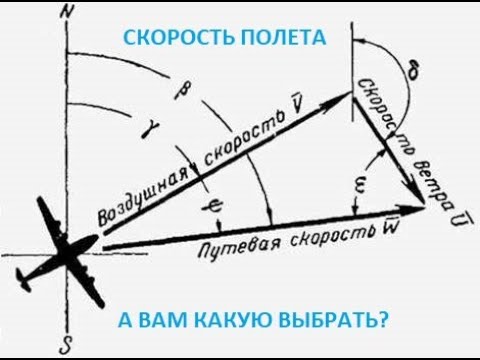
В общем случае .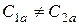

Треугольники скоростей занимают особое место в теории ступени турбомашин – по их характеру можно получить практически полную информацию о характеристиках ступени. А именно:

— вычислить работу, совершаемую ступенью, и ее мощность;

— вычислить КПД ступени;

— определить к какому типу относиться ступень: активному или реактивному;

— определить степень оптимальности той работы, которая приходится на данную ступень (недогружена или перегружена ступень);

— можно оценить форму профилей сопловой и рабочей лопатки.