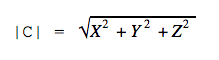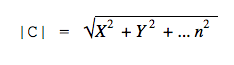Длина суммы векторов длиннее суммы длин самих векторов

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Определения скалярного произведения векторов через угол между ними

Сложение векторов по правилу треугольника (суммой векторов и называется вектор , начало которого совпадает с началом вектора , а конец — с концом вектора , при условии, что начало вектора приложено к концу вектора ) даёт возможность упрощать выражение перед вычислением произведений векторов.

Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются) даёт возможность узнать, как расположен относительно начала координат вектор, являющийся суммой слагаемых векторов. Подробно эти две операции разбирались на уроке «Векторы и операции над векторами».

Теперь же нам предстоит узнать, как найти длину вектора, являющегося результатом сложения векторов. Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из пункта A в пункт С — не прямая, а отклоняется от прямой, чтобы пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги. Кстати, геодезия — одна из тех сфер деятельности, где тригонометрические функции применяются во всех их полноте.

При сложении векторов для нахождения длины суммы векторов используется теорема косинусов. Пусть и — векторы, — угол между ними, а — сумма векторов как результат сложения векторов по правилу треугольника. Тогда верно следующее соотношение:

,

где — угол, смежный с углом . У смежных углов одна сторона общая, а другие стороны лежат на одной прямой (см. рисунок выше).

Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:

.

В случае вычитания векторов () происходит сложение вектора с вектором , противоположным вектору , то есть имеющим ту же длину, но противоположным по направлению. Углы между и и и между и являются смежными углами, у них, как уже было отмечено, одна сторона общая, а другие стороны лежат на одной прямой. В случае вычитания векторов для нахождения длины разности векторов нужно знать следующее свойство косинусов смежных углов:

косинусы смежных углов равны по абсолютной величине (величине по модулю), но имеют противоположные знаки.

Перейдём к примерам.

Видео:Сложение векторов. 9 класс.Скачать

Сложение векторов — решение примеров

Пример 1. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .

Решение. Из элементарной тригонометрии известно, что .

Шаг 1. Выполняем сложение векторов. Находим длину суммы векторов, поставляя в формулу длины косинус угла, смежного с углом между векторами:

Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:

Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение

Пример 2. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .

Пример 3. Даны длины векторов и длина их суммы . Найти длину их разности .

Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:

Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус «изначального» угла будет со знаком плюс.

Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:

Пример 4. Даны длины векторов и длина их разности . Найти длину их суммы .

Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус «изначального» угла (задача обратная по отношению к примеру 1) и находим его:

Шаг 2. Меняем знак косинуса и получаем косинус смежного угла между и :

Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:

Пример 5. Векторы и взаимно перпендикулярны, а их длины . Найти длину их суммы и и длину их разности .

Два смежных угла, как нетрудно догадаться из приведённого в начале урока определения, в сумме составляют 180 градусов. Следовательно, смежный с прямым углом (90 градусов) угол — тоже прямой (тоже 90 градусов). Косинус такого угла равен нулю, то же самое относится и к косинусу смежного угла. Поэтому, подставляя это значение в выражения под корнем в формуле длины суммы и разности векторов, получаем нули как последние выражения — произведения под знаком корня. То есть длины суммы и разности данных векторов равны, вычисляем их:

Пример 6. Какому условию должны удовлетворять векторы и , чтобы имели место слелующие соотношения:

1) длина суммы векторов равна длине разности векторов, т. е. ,

2) длина суммы векторов больше длины разности векторов, т. е. ,

3) длина суммы векторов меньше длины разности векторов, т. е. ?

Находим условие для первого соотношения. Для этого решаем следующее уравнение:

То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.

Находим условие для второго соотношения. Решаем уравнение:

Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).

Находим условие для третьего соотношения. Решаем уравнение:

Найденное условие выполняется, когда косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовали тупой угол.

Видео:8 класс, 43 урок, Сумма двух векторовСкачать

ЗАДАЧА 19
огэ

Задачи разделены на уровни сложности. Задачи из любого уровня вполне реально встретить на настоящем экзамене ОГЭ, более сложные встретятся если «не повезло».

Сложность у всех задач примерно одинаковая

1. Какое из следующих утверждений верно?
   1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны.
   2) Сумма углов прямоугольного треугольника равна 180°.
   3) Любая медиана равнобедренного треугольника является его высотой.

В ответе запишите номер выбранного утверждения.

Какие из следующих утверждений верны?
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) В любом параллелограмме есть два равных угла.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какое из следующих утверждений верно?
1) Дана окружность. Через любую точку плоскости можно провести к ней касательную прямую.
2) Если в параллелограмме некоторый угол равен 90°, то это квадрат.
3) В любом ромбе найдется угол меньше 120°.

В ответе запишите номер выбранного утверждения.

Какое из следующих утверждений верно?
1) Внутренние односторонние углы при пересечении параллельных прямых секущей равны.
2) Площадь трапеции равна произведению высоты на сумму оснований.
3) В любом квадрате все углы равны.

В ответе запишите номер выбранного утверждения.

Какие из следующих утверждений верны?
1) Сумма катетов длиннее гипотенузы.
2) Длина суммы векторов длиннее суммы длин самих векторов.
3) В любом треугольнике найдется острый угол.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какое из следующих утверждений верно?
1) Сумма длин трех сторон четырехугольника всегда длиннее четвертой стороны.
2) В любой выпуклый четырехугольник можно вписать окружность.
3) Диагонали ромба равны.

В ответе запишите номер выбранного утверждения.

Какое из следующих утверждений верно?
1) Площадь треугольника равна произведению стороны на высоту, проведенную к этой стороне.
2) Треугольники равны, если их соответствующие стороны равны.
3) У подобных треугольников площади равны.

В ответе запишите номер выбранного утверждения.

Какое из следующих утверждений верно?
1) Сумма вертикальных углов равна 180°.
2) Корень квадратный из площади квадрата равен длине его стороны.
3) Периметр прямоугольника всегда больше его площади.

В ответе запишите номер выбранного утверждения.

Какие из следующих утверждений верны?
1) У подобных треугольников соответствующие углы равны.
2) В правильном пятиугольнике все углы равны.
3) Площадь прямоугольника равна квадрату любой его стороны.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какое из следующих утверждений верно?
1) В правильном шестиугольнике все углы по 160°.
2) Не существует треугольника со сторонами 10,12 и 16.
3) Диагонали прямоугольника равны.

В ответе запишите номер выбранного утверждения.

Какие из следующих утверждений верны?
1) В любой прямоугольник можно вписать окружность.
2) Вписанные углы, опирающиеся на одну дугу окружности, равны.
3) Если угол между векторами равен 90°, то их скалярное произведение равно нулю.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какое из следующих утверждений верно?
1) Косинус угла в прямоугольном треугольнике это отношение прилежащего катета к противолежащему катету.
2) Катет лежащий против угла в 60° в два раза короче гипотенузы.
3) Диагонали ромба перпендикулярны.

В ответе запишите номер выбранного утверждения.

Какие из следующих утверждений верны?
1) Центр окружности вписанной в треугольник находится на пересечении биссектрис.
2) В правильном шестиугольнике все стороны равны.
3) Сумма двух соседних углов параллелограмма равна 180°.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какие из следующих утверждений верны?
1) Дана прямая. Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
2) Высоты треугольника пересекаются в одной точке.
3) Высота треугольника всегда лежит внутри треугольника.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какое из следующих утверждений верно?
1) Диагонали ромба пересекаются и точкой пересечения делятся пополам.
2) Площадь прямоугольника равна произведению двух противоположных сторон.
3) Длина вектора равна сумме квадратов его координат.

В ответе запишите номер выбранного утверждения.

Какое из следующих утверждений верно?
1) Сумма смежных углов равна 180°.
2) Если скалярное произведение векторов равно нулю, то векторы параллельны.
3) В любой трапеции есть, по крайней мере, два острых угла.

В ответе запишите номер выбранного утверждения.

Какие из следующих утверждений верны?
1) Площадь любого треугольника равна половине произведения сторон на синус угла между ними.
2) Все точки лежащие на биссектрисе некоторого угла равноудалены от сторон этого угла.
3) Площадь ромба равна половине произведения сторон.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какое из следующих утверждений верно?
1) Если две окружности касаются, то у них радиусы равны.
2) Периметр прямоугольника равен произведению двух соседних сторон.
3) Сумма углов пятиугольника равна 540°.

В ответе запишите номер выбранного утверждения.

Какие из следующих утверждений верны?
1) Вокруг любого четырехугольника можно описать окружность.
2) Если некоторая окружность касается прямой, то расстояние от центра окружности до этой прямой равно радиусу окружности.
3) Если соответственные углы при пересечении двух прямых секущей равны, то прямые параллельны.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какие из следующих утверждений верны?
1) Через точку, лежащую на окружности, всегда можно провести касательную к этой окружности.
2) Длина окружности всегда больше ее радиуса.
3) Если в треугольнике одна сторона равна половине второй, то в треугольнике есть угол в 30°.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какое из следующих утверждений верно?
1) Если в параллелограмме все углы равны, то это квадрат.
2) Длина самой длинной стороны в треугольнике меньше суммы длин двух других сторон.
3) Вокруг любого четырехугольника можно описать окружность.

В ответе запишите номер выбранного утверждения.

Какие из следующих утверждений верны?
1) Диагональ параллелограмма делит его на два равных треугольника.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какие из следующих утверждений верны?
1) В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3) Любой квадрат является прямоугольником.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какие из следующих утверждений верны?
1) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
2) Каждая из биссектрис равнобедренного треугольника является его медианой.
3) В любой ромб можно вписать окружность.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какие из следующих утверждений верны?
1) Любые два прямоугольных треугольника подобны.
2) Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.
3) Стороны треугольника пропорциональны синусам противолежащих углов.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какие из следующих утверждений верны?
1) Треугольник со сторонами, длины которых равны 3,4 и 5, является тупоугольным.
2) Прямоугольник обладает центром симметрии.
3) Любой прямоугольный треугольник не обладает центром симметрии.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какие из следующих утверждений верны?
1) У квадрата ровно две оси симметрии.
2) Центром симметрии ромба является точка пересечения его диагоналей.
3) Площадь прямоугольного треугольника меньше произведения его катетов.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какое из следующих утверждений верно?
1) В правильный шестиугольник всегда можно вписать окружность.
2) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
3) Сумма вертикальных углов равна 180°.

В ответ запишите номер выбранного утверждения.

Какое из следующих утверждений верно?
1) Через любые две точки на плоскости можно провести окружность, причем только одну.
2) У прямоугольного треугольника не может быть оси симметрии.
3) Диагонали трапеции всегда пересекаются.

В ответ запишите номер выбранного утверждения.

Какие из следующих утверждений верны?
1) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат.
2) В параллелограмме есть два равных угла.
3) Площадь параллелограмма меньше или равна произведению двух его соседних сторон.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какие из следующих утверждений верны?
1) Косинус острого угла прямоугольного треугольника равен отношению катета, прилежащего к этому углу, к гипотенузе.
2) Если в параллелограмме все углы равны, то это прямоугольник.
3) Все высоты равнобедренного треугольника лежать внутри этого треугольника.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Какое из следующих утверждений верно?
1) К двум окружностям всегда можно провести две общие касательные.
2) Если в четырехугольнике две противоположные стороны равны, то этот четырехугольник – параллелограмм.
3) Точка пересечения биссектрис любого треугольника всегда лежит внутри этого треугольника.

В ответ запишите номер выбранного утверждения.

Видео:СУММА ВЕКТОРОВ правило треугольникаСкачать

Операции с векторами

Как сложить и перемножить векторы (и зачем).

Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.

Напомним основные мысли:

• Вектор — это абстрактное понятие, которое представляет собой организованную последовательность каких-то чисел.
• В виде вектора можно представить координаты предмета в каком-то пространстве; площадь квартиры и её стоимость; цифровые данные анкеты какого-то человека и динамику цен на нефть.
• Если по-простому, то векторы нужны, чтобы обрабатывать большое количество организованных чисел. Представьте, что вектор — это коробка с конфетами, только вместо конфет — числа. Каждое число стоит в своей ячейке.
• Машинное обучение основано на перемножении матриц, которые, в свою очередь, можно представить как наборы векторов. Так что векторы лежат в глубине всех модных и молодёжных технологий ИИ.

С векторами можно совершать некоторые математические операции. Вот о них и поговорим.

Видео:Нахождение длины вектора через координаты. Практическая часть. 9 класс.Скачать

Правильно — векторы

Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».

Видео:ВЕКТОРЫ 9 класс С НУЛЯ | Математика ОГЭ 2023 | УмскулСкачать

Сложение

Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.

Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).

Векторы X, Y, Z, K в двухмерном пространстве

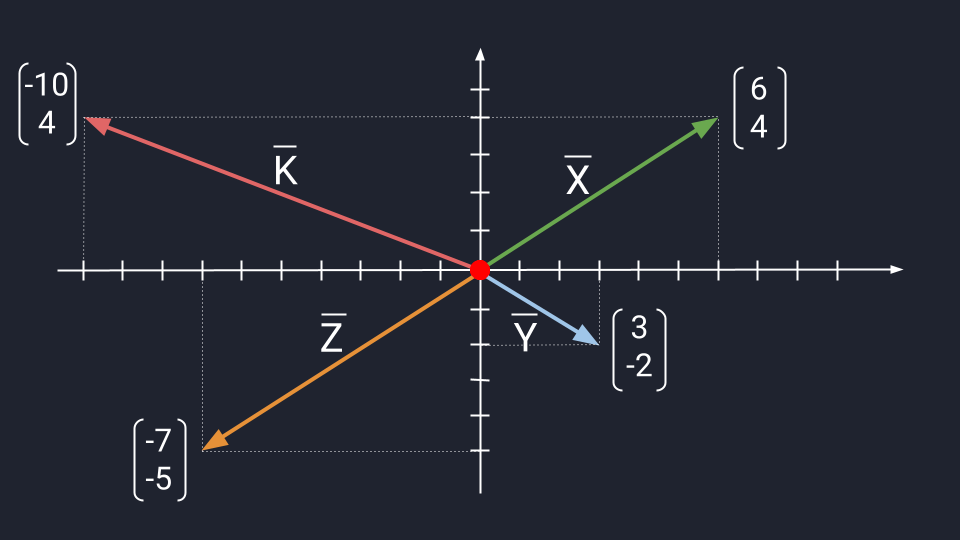
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.

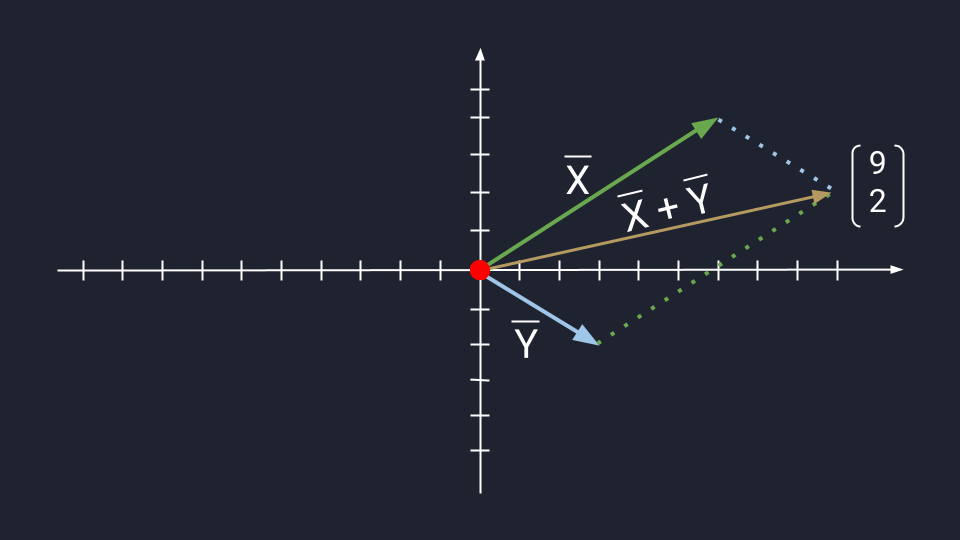
Предположим, нам нужно сложить векторы X и Y.

X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)

Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.

Например, вот сложение векторов с пятью координатами:

X = (6, 4, 11, 14, 99)
Y = (3, -2, 10, -10, 1)
X + Y = (9, 2, 21, 4, 100)

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Интуитивное изображение сложения

Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.

Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.

Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.

Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)

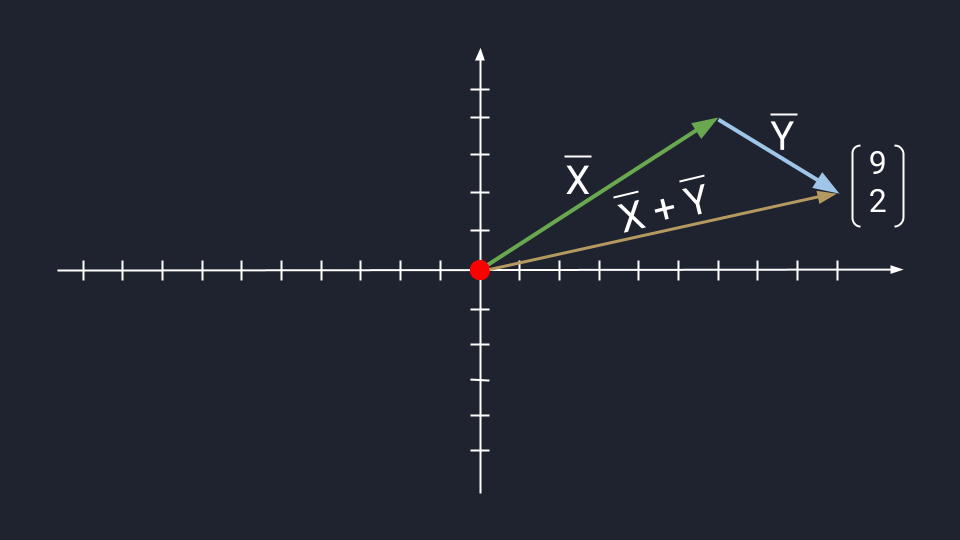
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.

Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.

Сложение векторов по методу параллелограмма: X = (6, 4); Y = (3, -2); Х + Y = (9, 2)

Видео:Длина вектора через координаты. 9 класс.Скачать

Вычитание

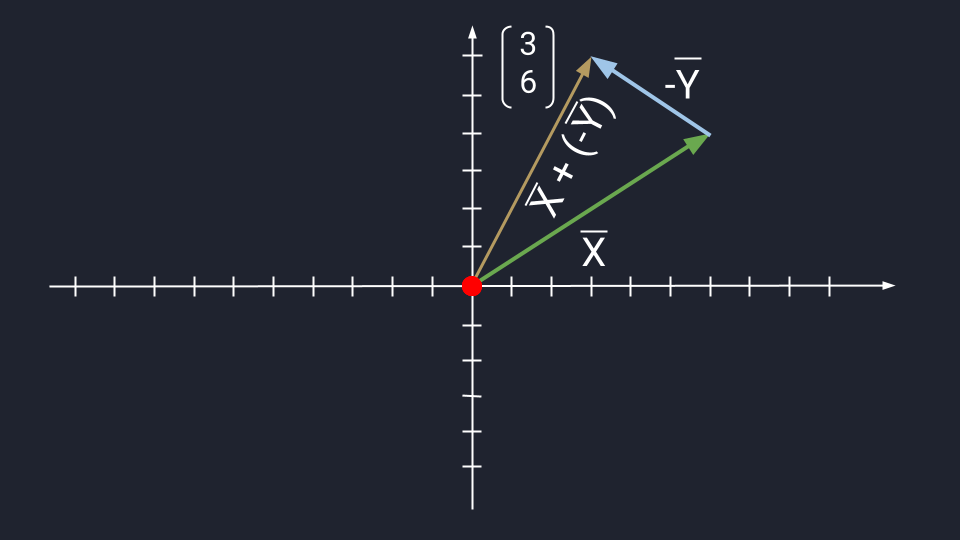
Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)

Дальше используются правила сложения. Пошагово это выглядит так:

1. У нас есть X = (6, 4) и Y = (3, −2).
2. Превращаем формулу Х − Y в формулу Х + (−Y).
3. Разворачиваем вектор Y. Было: Y = (3, −2). Стало: −Y = (−3, 2).
4. Считаем: X + (−Y) = (3, 6).

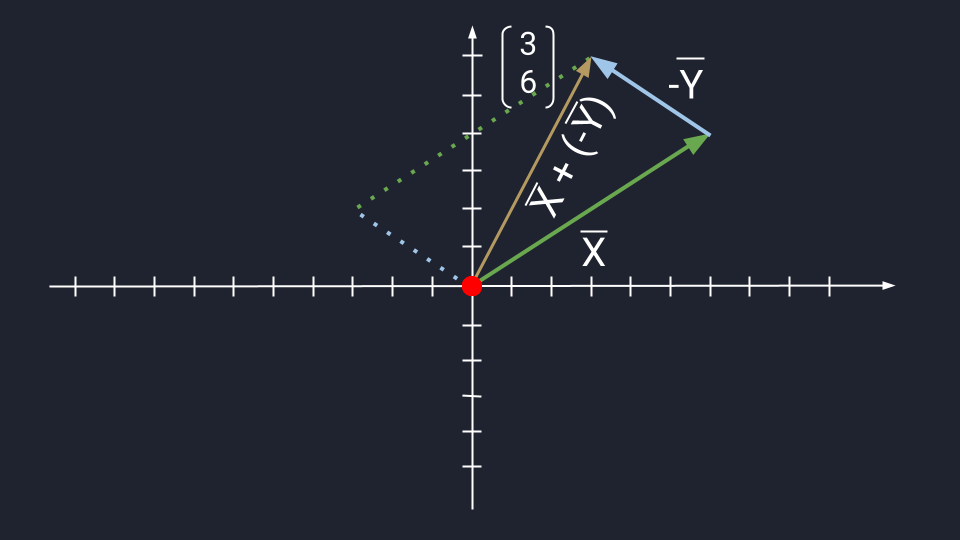
Теперь посмотрим, как выглядит вычитание векторов на графике:

Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Длина вектора

Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.

Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:

X = 6 − 2 = 4
Y = 5 − 2 = 3

Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:

|C|2 = 42 + 32 = 25
|C| = √25 = 5 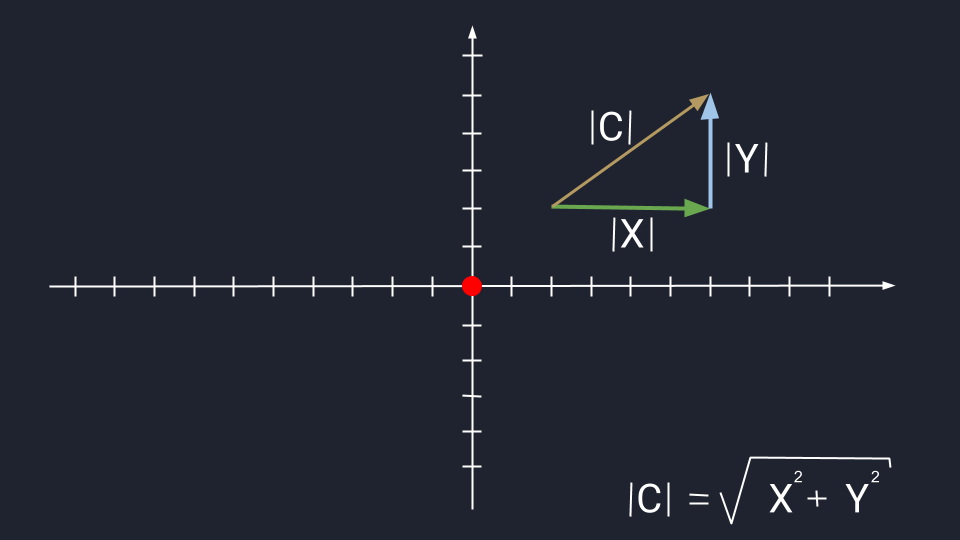Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат

Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.

В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.

Видео:Геометрия 9 класс (Урок№2 - Сумма двух векторов. Законы сложения векторов.)Скачать

Умножение и деление вектора на число

Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.

Умножение вектора на число

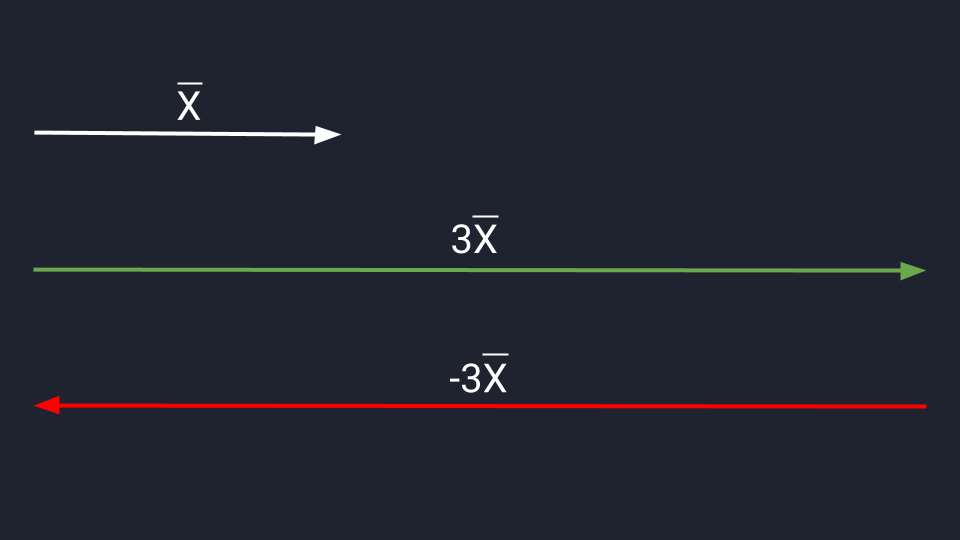
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.

Деление вектора на число

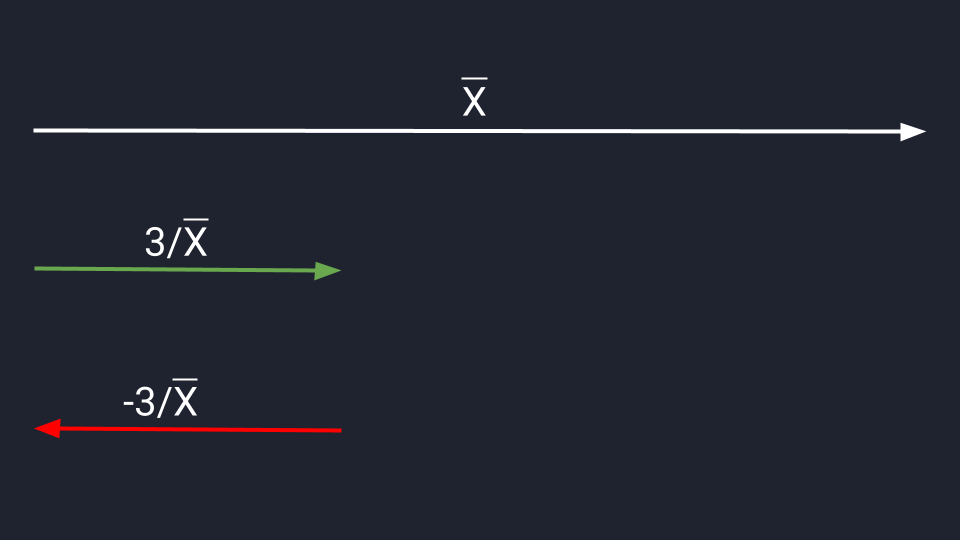
Видео:Все типы 2 задание векторы ЕГЭ по математике профиль 2024Скачать

Да вроде несложно!

Пока ничего сложного. Но если углубляться, вы узнаете, что:

• векторы можно умножать на векторы тремя способами в зависимости от задачи и от того, что мы понимаем под умножением;
• если от векторов перейти к матрицам, то перемножение матриц имеет несколько более сложную и довольно неинтуитивную математику;
• а перемножение матриц — это и есть машинное обучение.

Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Что дальше

В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.

💥 Видео

2. Space Engineers, KSP, FTD: длина вектора, умножение на скаляр, нормализация, сумма векторовСкачать

Сложение и вычитание векторов. Практическая часть. 11 класс.Скачать

10 класс, 41 урок, Сумма нескольких векторовСкачать

Сложение и вычитание векторов через координаты. Практическая часть. 11 класс.Скачать

Выразить векторы. Разложить векторы. Задачи по рисункам. ГеометрияСкачать

Задача на вычисление суммы векторовСкачать

8 класс, 45 урок, Сумма нескольких векторовСкачать