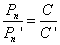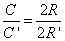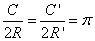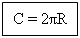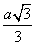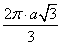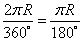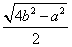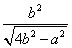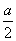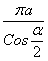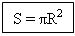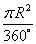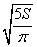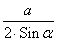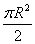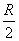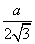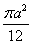Основные определения и свойства. Число π Основные определения и свойства. Число π |
 Формулы для площади круга и его частей Формулы для площади круга и его частей |
 Формулы для длины окружности и ее дуг Формулы для длины окружности и ее дуг |
 Площадь круга Площадь круга |
 Длина окружности Длина окружности |
 Длина дуги Длина дуги |
 Площадь сектора Площадь сектора |
 Площадь сегмента Площадь сегмента |
- Основные определения и свойства
- Формулы для площади круга и его частей
- Формулы для длины окружности и её дуг
- Площадь круга
- Длина окружности
- Длина дуги
- Площадь сектора
- Площадь сегмента
- Геометрия. Урок 5. Окружность
- Определение окружности
- Отрезки в окружности
- Дуга в окружности
- Углы в окружности
- Длина окружности, длина дуги
- Площадь круга и его частей
- Теорема синусов
- Примеры решений заданий из ОГЭ
- Длина окружности, площадь круга и кругового сектора
- Корзина
- Площадь круга
- Площадь сектора круга
Видео:Геометрия 9 класс (Урок№24 - Площадь круга. Площадь кругового сектора.)Скачать

Основные определения и свойства
| Фигура | Рисунок | Определения и свойства | ||||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||||
| Дуга |  | |||||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||||
| Сектор |  | |||||||||||||||||||||||||||||
| Сегмент |  | |||||||||||||||||||||||||||||
| Правильный многоугольник |  | |||||||||||||||||||||||||||||
 |
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Часть окружности, расположенная между двумя точками окружности

Конечная часть плоскости, ограниченная окружностью

Часть круга, ограниченная двумя радиусами

Часть круга, ограниченная хордой

Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Формулы для площади круга и его частей
| Числовая характеристика | Рисунок | Формула | |||||||||||||
| Площадь круга |  | ||||||||||||||
| Площадь сектора |  | ||||||||||||||
| Площадь сегмента |  |
| Площадь круга |
 |

где R – радиус круга, D – диаметр круга


если величина угла α выражена в радианах

если величина угла α выражена в градусах


если величина угла α выражена в радианах

если величина угла α выражена в градусах
Видео:ГЕОМЕТРИЯ 9 класс: Длина окружности, площадь круга и площадь кругового сектораСкачать

Формулы для длины окружности и её дуг
| Числовая характеристика | Рисунок | Формула | ||
| Длина окружности |  | |||
| Длина дуги |  |
| Длина окружности |
 |
где R – радиус круга, D – диаметр круга

если величина угла α выражена в радианах

если величина угла α выражена в градусах
Видео:Длина окружности и площадь круга. Площадь кругового сектора. Урок 13. Геометрия 9 классСкачать

Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Видео:Геометрия 9 класс (Урок№25 - Решение задач с исп.форм.длины окр.,площади круга и кругового сектора.)Скачать

Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Видео:ДЛИНА ОКРУЖНОСТИ и ПЛОЩАДЬ КРУГА 9 класс геометрия АтанасянСкачать

Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Видео:Площадь сектора и сегмента. 9 класс.Скачать

Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
Видео:Длина окружности и площадь круга. Урок 12. Геометрия 9 классСкачать

Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
Видео:Решение задач с использованием формулы длины окружности, площади круга и кругового сектораСкачать

Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .
Видео:Площадь кругового сектора | Геометрия 7-9 класс #111 | ИнфоурокСкачать

Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Видео:Площадь круга. 9 класс.Скачать

Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Видео:9 класс, 28 урок, Площадь кругового сектораСкачать

Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Видео:Геометрия 9 класс (Урок№23 - Длина окружности.)Скачать

Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Видео:Математика 6 класс (Урок№76 - Длина окружности. Площадь круга.)Скачать

Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Видео:Длина окружности. 9 класс.Скачать

Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Видео:Длина окружности. Площадь круга.Скачать

Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Видео:Длина окружности. Площадь круга, 6 классСкачать

Длина окружности, площадь круга и кругового сектора
Корзина

Теоретический урок по предмету математики для решения задач по теме «Длина круга и площадь кругового сектора».
Содержание данной онлайн страницы электронного справочника для школьников:
- – тема «Длина окружности» представлена на примере решения задач 124 — 129;
- – в контрольных работах с номерами 130 — 138 данной рабочей тетради по математике рассматривается, как находить площадь круга и сектора окружности.
Вывод формулы длины окружности.
Пусть C и C′ — длины окружностей радиусов R и R′. Впишем в окружности правильные многоугольники.
Pn = n • an = n • 2R • Sin 
Pn′ = n • an = n • 2R′ • Sin 
Тогда 
Зная, что периметры Pn и Pn′ — приближенные значения длин окружностей C и C′, при n →∞, получаем

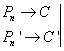



Но в силу равенства 
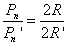

По свойству пропорции 
Значение величины π («пи») приближенно равно 3,14.

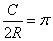


Формула длины окружности:

Задача 124.
Если известен радиус R = 4, то длина окружности C = 2πR = 2 • 3,14 • 4 = 25,12
Если C = 82, то радиус окружности R = 
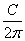

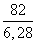
Если C = 18π, то радиус окружности R = 
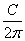

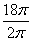
Задача 125.
a — сторона правильного треугольника
Найдите: длину описанной окружности
an = 2R • Sin ( 
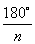
a = R 
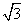



Тогда длина окружности, описанной около правильного треугольника равна C = 2πR = 
Вывод формулы для вычисления дуги L с градусной мерой α. 
Градусная мера окружности 360°,
Длина окружности C = 2πR
Длина дуги в 1° равна 
Тогда длина дуги окружности в α градусах: 
Задача 126.
| 1) α = 30° | 2) α = 45° | 3) α = 60° | 4) α = 90° |
Найти: длину дуги окружности
1) L = 
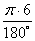

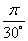
2) L = 
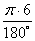

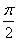
3) L = 
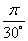
4) L = 
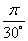
Задача 127.
ABCDEF — правильный шестиугольник,
площадь шестиугольника S6 = 24 
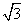
Найти: чему равна длина описанной окружности C = ?
Значит, нужно найти радиус описанной окружности.
Площадь шестиугольника определяется по формуле
S6 = 

Радиус вписанной окружности определяется по формуле
r6 = R • Cos 
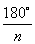

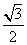
Сторона шестиугольника равна радиусу описанной окружности: a6 = R
Тогда периметр шестиугольника P6 = 6 • a6 = 6R (см)
S6 = 




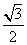

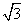
24 
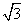

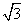
R 2 = 
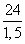


R = 
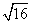
Тогда длина описанной окружности равна
C = 2πR = 2π • 4 = 8π (см)
Задача 128.
сторона квадрата AB = a
Найти: длину вписанной окружности C = 2π • r = ?
r4 = R • Cos 
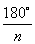

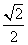
C = 2π • r = 2π • 
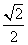

AB = a = 2r = R 
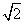

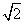
Ответ: длина окружности, вписанной в квадрат C = π • a
Задача 129.
Дано: окружность (O; R) – описанная около следующих фигур
1) Δ ABC – вписанный прямоугольный треугольник;
2) Δ ABC – вписанный равнобедренный треугольник;
a – основание, b – сторона
3) ABCD – вписанный прямоугольник,
BC = a – сторона прямоугольника,
α – острый угол между диагоналями
Найти: длину описанной окружности C = 2πR = ?
2R = AB 




AB = 
Тогда длина окружности, описанной около прямоугольного треугольника
C = 2π • 


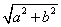

BH = 
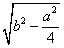


Площадь треугольника равна половине произведения основания на высоту
SΔABC = 


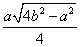
Но площадь треугольника можно также найти через деление произведения трех его сторон на четыре радиуса описанной окружности:
SΔABC = 
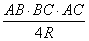

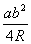
Используя равенства (1) и (2), получаем

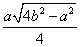

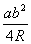



Тогда длина окружности, описанной около равнобедренного треугольника
C = 2π • 


OB = OC = OA = OD = R
Проведем OH – высота и биссектриса равнобедренного треугольника ΔAOD.
Рассмотрим прямоугольный треугольник ΔOHD.



















AH = HD = 
Cos 


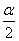

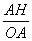

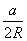

R = 
Тогда длина окружности, описанной около прямоугольника
C = 2π • 
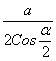

Видео:Длина окружности и площадь кругаСкачать

Площадь круга
S – площадь круга
Sn′ – площадь малого круга


Рассмотрим правильный многоугольник (см. рисунок).
Площадь круга больше площади многоугольника:
Sn 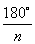
При n→∞ косинус Cos ( 
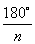
Следовательно, Sn′ → S при n→∞.
Из неравенства (1) следует Sn → S при n→∞.
Мы знаем, что площадь правильного многоугольника
Sn = 

Учитывая, что rn → R, Pn → 2πR, Sn → S при n→∞.
Тогда S = 



Формула площади круга:

Видео:Площадь круга. Площадь кругового сектораСкачать

Площадь сектора круга
Определение:
Сектором круга или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

πR 2 – площадь круга.
Площадь кругового сектора, мера которого 1°, равна 
Площадь кругового сектора, мера которого α градусов, равна 
Формула площади сектора круга:

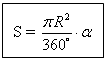
α – градусная мера дуги.
Задача 130.


S – площадь кругового сектора
Найдите: R – радиус окружности
S = 
360° • S = πR 2 • α
R 2 = 
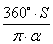

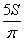



Ответ: радиус равен R = 

Задача 131.
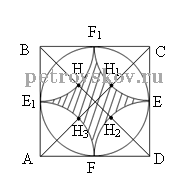
сторона квадрата AB = a
S = 
Рассмотрим на рисунке сектор FAE1H3, где AF = AH3 = R = 
S = 
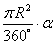



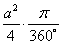

Площадь четырех секторов:
S1+2+3+4 = 4 • 
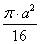

SABCD = 

Рассмотрим ΔACD, где AD = CD = a.
По теореме Пифагора:
AC = 
Тогда Sn= 


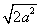

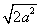
Следовательно, площадь заштрихованной фигуры
SEFE 1F 1 = SABCD – S 1+2+3+4 = a 2 – 
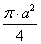

Ответ: 
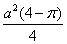


Найти: площадь окружности (O;OH1),
площадь каждой из трех мишеней = ?
Sокр1 = πR 2 = π • (OH1) 2 = π • 1 = π
Sокр2 = πR 2 = π • (OH2) 2 = π • 4 = 4π
Sокр3 = πR 2 = π • (OH3) 2 = π • 9 = 9π
Sокр4 = πR 2 = π • (OH4) 2 = π • 16 = 16π
Задача 133.
круг (O;R), описанный около четырехугольника и треугольника
1) ABCD – прямоугольник,
a и b – стороны прямоугольника


α – противолежащий угол
Найти: площадь круга, изображенного на рисунке.
Рассмотрим треугольник ΔABD – прямоугольный.
По теореме Пифагора:
BD 2 = AB 2 + AD 2
R 2 = 



Найдем площадь круга через его диаметр AB = 2AO = R
Sin α = 
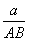



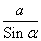

2R = 
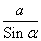



S = πR 2 = π • 
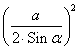

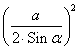

Ответ: 1) π • 
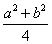

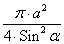
Задача 134.








Сумма площади полукруга на гипотенузе равна сумме площадей полукругов на катетах
Пусть AB = c; AC = a; BC = b.
Формула площади сектора круга
S = 
S = 
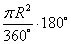

S1 = 
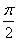





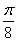
S2 = 
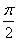





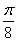
S3 = 
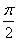





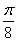
Тогда S2 + S3 = 
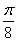

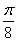

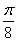
По теореме Пифагора:
S2 + S3 = 
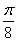

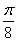
Задача 135.



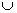


чему равна площадь сектора круга с дугой ALB = ?
Градусная мера дуги

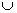
Тогда площадь сектора круга
S = 
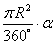

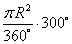

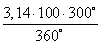
Ответ: площадь сегмента круга S ≈ 262 см 2 .
Задача 136.
круг (O; OH) вписан в ΔABC –

Найти: чему равна площадь круга
Рассмотрим треугольник ΔABH – прямоугольный.
AO – биссектриса угла 

Значит, 

OH = 

r = 


Sin 60° = 
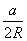



Тогда радиус вписанного круга r = 
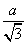

Следовательно, площадь круга S = πr 2 = 
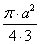

Ответ: Sкруга = 

Задача 137.
Малый круг (O; OD)
Площадь большого круга
Диаметр малого круга
Найти: разницу диаметров



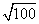
D2 = 2R = 2 • 9,25 = 18,5 (мм)
Задача 138.
Малый круг (O; OH) – отверстие трубы
Радиус малой трубы OH = 3м
Разница диаметров между двумя трубами AB = 1м


Найти: сколько нужно песка, чтобы заполнить пространство между двумя трубами
Рассмотрим круг′ (O; OH).
Площадь данного круга:
S′ = πR 2 = 9 • 3,14 ≈ 28,26 (м 2 )
Рассмотрим круг′′ (O; OH+AB).
S′′ = πR 2 = 16 • 3,14 ≈ 50,24 (м 2 )
Тогда площадь между двумя трубами
S = S′′ – S′ = 50,24 – 28,26 ≈ 21,98 (м 2 )