Длина хорды равностороннего треугольника

В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.

Видео:Формулы равностороннего треугольника #shortsСкачать

Определение равностороннего треугольника

Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.

Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.

Видео:№706. Найдите сторону равностороннего треугольника, если радиус описанной около него окружностиСкачать

Свойства равностороннего треугольника

Свойство 1

В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.

Свойство 2

В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.

CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.

Свойство 3

В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.

Свойство 4

Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.

Свойство 5

Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.

• R – радиус описанной окружности;
• r – радиус вписанной окружности;
• R = 2r.

Свойство 6

В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:

1. Высоту/медиану/биссектрису:

2. Радиус вписанной окружности:

3. Радиус описанной окружности:

4. Периметр:

5. Площадь:

Видео:ОГЭ ЗАДАНИЕ 16 НАЙДИТЕ ДЛИНУ ХОРДЫ ОКРУЖНОСТИ ЕСЛИ РАДИУС 13 РАССТОЯНИЕ ДО ХОРДЫ 5Скачать

Пример задачи

Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.

Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:

Видео:Окружность. Длина хорды. Теорема синусов.Скачать

Чему равна длина хорды?

Видео:ЕГЭ-2022 ||Задание №6 || Найти длину хордыСкачать

Что такое хорда 7 класс?

Отрезок, соединяющий любые две точки окружности, называют хордой. Хорда, проходящая через центр окружности, называется диаметром. . Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом.

Видео:Как найти длину хорды по радиусу и центральному углу. Геометрия 8-9 классСкачать

Чему равна длина окружности?

Длина окружности круга равна двум пи умноженным на радиус.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Что такое хорда и её свойства?

Хордой называется отрезок, соединяющий две точки окружности. Если хорда проходит через центр окружности, то она называется диаметром. Хорда является частью секущей окружности.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Что такое хорда в математике 5 класс?

Хорда окружности – это отрезок, соединяющий какие-нибудь две точки окружности. Диаметр окружности – это хорда, проходящая через центр окружности.

Видео:Окружнось. Зависимость длины хорды, от длины дуги.Скачать

Что такое хорда в теле человека?

(математическая), прямолинейный отрезок, соединяющий две произвольные точки кривой линии или поверхности. спинная струна, эластичная несегментированная скелетная ось у хордовых (См. Хордовые) животных и человека.

Видео:Равносторонний треугольник и три хорды в описанной окружностиСкачать

Какая формула описывает длину окружности?

= π. Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам.

Видео:7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Чему равна длина окружности диаметр которой равен 1 м?

Для нахождения длины окружности применяется формула: l = 2πr = πd. Если диаметр составляет 1 м, то длина окружности будет равна: 3,14 * 1 = 3,14 (м).

Видео:Задача на нахождение длины хорды окружностиСкачать

Как доказать что хорды одинаковые?

Если хорды равноудалены от центра окружности, то они равны. Если хорды равны, то они равноудалены от центра окружности. Большая из двух хорд находится ближе к центру окружности.

Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

В каком случае хорда равна радиусу?

Если хорда равна радиусу окружности, то она стягивает дугу 60º. AB — хорда, AB=R. . OA=OB=R, хорда AB по условию также равна радиусу: AB=R, следовательно, AB=OA=OB, то есть треугольник AOB — равносторонний. Отсюда, ∠AOB=60º (как угол равностороннего треугольника).

Видео:Деление окружности на равные части. Внимание!!! В таблице имеются ошибки. ПОЛЬЗУЙТЕСЬ ФОРМУЛОЙ!!!Скачать

Как делить хорду Диаметр перпендикулярный ей?

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые её дуги пополам. Диаметр, проходящий через середину хорды, перпендикулярен к ней и делит стягиваемые ею дуги пополам.

Видео:Нахождение стороны прямоугольного треугольникаСкачать

Формула длины хорды окружности

Хорда — отрезок соединяющий любые две точки окружности. Диаметр окружности, самая большая хорда.

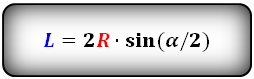
L — хорда

R — радиус окружности

O — центр окружности

α — центральный угол

Формула длины хорды, ( L ):

Калькулятор для расчета длины хорды окружности :

Дополнительные формулы для окружности:

🔍 Видео

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Геометрия Равносторонний треугольникСкачать

Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора | Геометрия | АлгебраСкачать

найти радиус окружности, описанной вокруг треугольникаСкачать

Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать