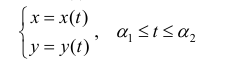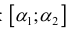Задачи на вычисление длины дуги кривой — однотипные. Существуют чёткие схемы для решения таких задач по формулам, которые отличаются в зависимости от того, какими и сколькими уравнениями задана кривая. Формулы представляют собой интегралы от корня, под которым в тех или иных сочетаниях присутствуют производные функций, которыми задана кривая. Следовательно, для того, чтобы вычислять длину дуги кривой, требуется уметь вычислять производные и интегралы. При вычислении интегралов возможны типичные трудности, связанные, например, с выбором подходящей подстановки. Эти задачи будем решать в примерах к данному уроку.
- Вычисление длины дуги кривой, заданной в прямоугольных координатах
- Вычисление длины дуги кривой, заданной параметрически
- Вычисление длины дуги кривой, заданной в полярных координатах
- Длина дуги кривой — определение и вычисление с примерами решения
- Вычисление длин дуг кривых
- Понятие спрямляемой кривой
- Достаточное условие спрямляемости кривой
- Необходимое и достаточное условие спрямляемости кривой
- 🔥 Видео
Видео:Длина дуги окружности. 9 класс.Скачать

Вычисление длины дуги кривой, заданной в прямоугольных координатах
Пусть в прямоугольных координатах на плоскости уравнением y = f(x) задана кривая.
Найдём длину дуги AB этой кривой, заключённой между вертикальными прямыми x = a и x = b (рисунок ниже).
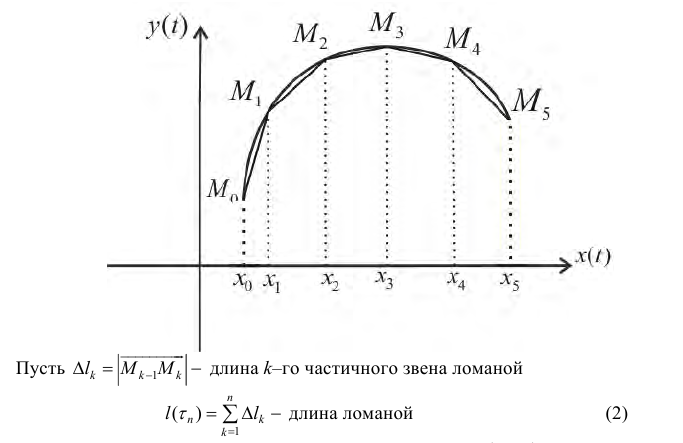
Возьмём на дуге AB точки A, M 1 , M 2 , . M i , . B с абсциссами x 0 = a, x 1 , x 2 , . x i , . b = x n и проведём хорды AM 1 , M 1 M 2 , . M n-1 B , длины которых обозначим соответственно через Δs 1 , Δs 2 , . Δs n . Тогда получим ломаную AM 1 M 2 . M n-1 B , вписанную в дугу AB. Длина ломаной равна

Длиной s дуги AB называется тот предел, к которому стремится длина вписанной ломаной, когда длина её наибольшего звена стремится к нулю:

Этот предел интегральной суммы равен определённому интегралу

Формула выше и есть формула для вычисления дуги кривой.
Пример 1. Найти длину дуги кривой 

Решение. Находим производную данной функции:
Используем формулу (1), подставляя найденную производную:
Ответ: длина дуги кривой равна 74.
Пример 2. Найти длину окружности 
Решение. Вычислим сначала длину четвёртой части окружности, лежащей в первом квадранте. Тогда уравнение дуги будет:

откуда находим производную функции:
Используем формулу (1) подставляя в неё производную, получаем:
Ответ: длина всей окружности равна 
Если в прямоугольных координатах уравнениями z = x(x) и y = y(x) задана пространственная кривая, то длина её дуги вычисляется по формуле:

Видео:Длина окружности. 9 класс.Скачать

Вычисление длины дуги кривой, заданной параметрически
Найдём теперь длину дуги кривой в том случае, когда кривая задана параметрическими уравнениями:
В этом случае длину дуги кривой следует находить по формуле

Пример 3. Найти длину дуги кривой, заданной параметрическими уравнениями
если 
Решение. Рассчитаем интервал, в котором будет меняться значение t, если 
Вычислим производные функций x и y:
Используем формулу (3):

Ответ: длина дуги кривой равна 26.
Если параметрическими уравнениями
задана пространственная кривая, то длина её дуги вычисляется по формуле:

Пример 4. Найти длину дуги винтовой линии, заданной параметрическими уравнениями
Решение. Вычислим производные функций x, y и z:
Используем формулу (4):
Видео:Нахождение длины дуги кривойСкачать

Вычисление длины дуги кривой, заданной в полярных координатах
Пусть кривая задана в полярных координатах:
Длина её дуги вычисляется по формуле:

Пример 5. Найти длину дуги кривой, заданной в полярных координатах 
Решение. Вычислим производную функции:

Заданная кривая — кардиоида (рисунок выше). Так как она симметрична, вычислим только ту часть длины дуги, у которой 

Видео:ДЛИНА ДУГИ окружности 9 класс Атанасян 1111 1112 длина окружностиСкачать

Длина дуги кривой — определение и вычисление с примерами решения
Длина дуги кривой:
Определение 1. Рассмотрим простую кривую L на плоскости (см. § 30), заданную параметрически в виде
Разобьем отрезок
Кривая называется спрямлякмой, если множество 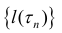
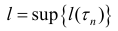
Замечание. Эквивалентное утверждение: число l называется длиной кривой L, если 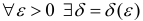
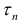
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Длина окружности. Математика 6 класс.Скачать

Вычисление длин дуг кривых
Видео:Длина дуги кривойСкачать

Понятие спрямляемой кривой
В школьном курсе математики рассматривался вопрос о вычислении длин отрезков прямой, длины окружности, а также различных ее частей. В приложениях математики возникает потребность в вычислении длин дуг произвольных кривых. Но, чтобы вычислить длину произвольной кривой, надо быть уверенным в том, что рассматриваемая кривая имеет конечную длину.
В средней школе длиной окружности называют предел последовательности периметров вписанных в окружность правильных многоугольников (при неограниченном удвоении числа сторон). Однако это определение неприменимо к произвольным кривым.
Дадим общее определение понятия длины кривой. Пусть задана жорданова кривая
Напомним, что функции и непрерывны на отрезке. Разобьем отрезок на части числами
Каждому числу соответствует точка кривой . Проводя отрезки , получим ломаную линию , вписанную в кривую . Обозначим ее длину через .
Определение. Жорданова кривая (1) называется спрямляемой (имеющей длину), если множество длин вписанных в эту кривую ломаных у ограничено сверху. Точная верхняя граница множества называется длиной кривой и обозначается
Докажем, что длина спрямляемой кривой обладает свойством аддитивности.
Пусть жорданова кривая разбита на кривые и . Если эти кривые спрямляемы, то кривая спрямляема, причем .
В самом деле, пусть — любая ломаная, вписанная в кривую , и пусть —точка, разбивающая на и . Добавляя эту точку к вершинам ломаной , получим ломаную , длина которой не меньше длины ломаной . Но ломаная состоит из двух частей и , вписанных соответственно в кривые и , причем и . Поэтому
Это неравенство показывает, что число является одной из верхних границ для множества длин ломаных, вписанных в кривую . Но для любого 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC4AAAAQBAMAAACb51DZAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/QHAQSFZiDGh0BCgsXHgm/CxLgAAALNJREFUGNNjYCAecHtgF8+vWYFNmEWCoX4DnOcOZ/IuYAhMANJMCiAem00AVFzRgEHxAlDAULYBJKsCk3C8wKD4iYFhborzA4i5xg4Q8QIGRSEGjglwK1gnOyGJm5VvQEgkwMVZPy8OgIufT4CaL8TA3IAw5zDYnI0GICe1w4VVDkPs1QK6/wFD1yalPIhzLKE61UQZHgYwsEsZgl3EZgmzhqn+uRiQCsuAhAPcdibVZxsYAOHLKP4AljeRAAAAAElFTkSuQmCC» /> найдутся ломаные и , вписанные в и , такие, что
Объединяя и , получаем ломаную , вписанную в и такую, что
А это и значит, что — точная верхняя граница множества , т. е. ‘ (Г) = / (Гх) + / (Г2).
Видео:Нахождение длины дуги кривой.Скачать

Достаточное условие спрямляемости кривой
Назовем жорданову кривую , регулярной, если функции и имеют на отрезке непрерывные производные. Справедлива следующая теорема.
Теорема 1. Всякая регулярная жорданова кривая спрямляема.
Доказательство. Разобьем отрезок на части точками и впишем в кривую ломаную, соответствующую этому разбиению. Рассмотрим одно звено этой ломаной, (рис. 49). Длина этого звена равна
Но по теореме Лагранжа найдутся такие и , что
Значит, длина всей ломаной выражается формулой
По условию производные и непрерывны на отрезке . Поэтому для и на отрезке есть наибольшие значения. Обозначим их и
Но тогда , а потому в силу (3)
Поскольку , то для всех ломаных, вписанных в кривую ,
Поэтому кривая спрямляема.
Отметим, что из равенства (3) вытекает также оценка длины ломаной снизу:
где и — наименьшие значения для и на отрезке .
Из неравенств (4) и (5) вытекают аналогичные неравенства для длины кривой
Неравенство (7) следует из неравенства (5) и из того, что . Чтобы доказать неравенство (6), заметим, что в силу неравенства (4) является одной из верхних границ для длин вписанных в ломаных, число же — точная верхняя граница для этих длин, т. е. наименьшая из верхних границ. Отсюда и следует неравенство (6).
Видео:Окружнось, дуга, длина дуги, центральный угол.Скачать

Необходимое и достаточное условие спрямляемости кривой
Данное ранее условие спрямляемости кривой является достаточным, но не необходимым (например, любая ломаная спрямляема, но не регулярна, так как имеет точки излома). Чтобы сформулировать необходимое и достаточное условие спрямляемости кривой, нам понадобится понятие: функция с ограниченным изменением.
Рассмотрим функцию , определенную на отрезке , и произвольное разбиение этого отрезка:
Для каждого частичного промежутка разбиения образуем разность — приращение функции на этом промежутке. Эта разность может быть как положительной, так и отрицательной. Заменим все эти разности их модулями и сложим их. Получим сумму
Полученная сумма называется изменением функции , соответствующим разбиению отрезка .
Рассмотрим множество изменений функции , соответствующих всевозможным разбиениям отрезка . Если это множество ограничено сверху, то говорят, что функция имеет ограниченное изменение на отрезке , а точную верхнюю границу этого множества называют изменением функции на отрезке и обозначают . Таким образом,
Теперь мы можем сформулировать и доказать необходимое и достаточное условие спрямляемости жордановой кривой.
Теорема 3. Для того чтобы жорданова кривая спрямляемой, необходимой достаточно, чтобы непрерывные функции и имели ограниченное изменение на отрезке .
Доказательство. Покажем сначала, что ограниченность изменения функций и на отрезке является необходимым условием спрямляемости кривой . В самом деле, если кривая спрямляема, то множество длин вписанных в нее ломаных ограничено сверху некоторым числом . Это означает, что для любой вписанной в ломаной имеем:
Но из рисунка 54 видно, что и , а потому
Эти неравенства можно переписать следующим образом:
Они показывают, что для любого разбиения отрезка имеем и , т. е. функции и имеют ограниченное изменение на отрезке .
Теперь докажем, что если функции и имеют ограниченное изменение на отрезке , то кривая спрямляема на этом отрезке. В самом деле, в этом случае существует такое число , что
Иными словами, и . Но из рисунка 54 видно, что
Поэтому для любой ломаной , вписанной в кривую , имеем:
Значит, множество ограничено сверху числом , и потому кривая спрямляема.
🔥 Видео
Длина дуги числовой окружности | Алгебра 10 класс #9 | ИнфоурокСкачать

№1109. Найдите длину дуги окружности радиуса 6 см, если ее градусная мера равна: а) 30°; б) 45°Скачать
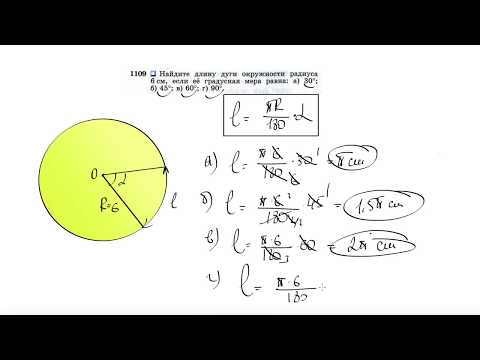
Как брать неберущийся интеграл Задача Найти длину дуги параболыСкачать

Окружнось. Зависимость длины хорды, от длины дуги.Скачать

Видеоурок "Длина дуги кривой"Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

Длина окружности и дугиСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Длина дуги окружности. Практическая часть. 9 класс.Скачать
Длина эллипса и разложение в ряд для эллиптического интегралаСкачать

Вычисление длины дугиСкачать

Длина дуги как доля длины окружности (видео 14) |Окружность и Круг | ГеометрияСкачать