Предложенные диктанты адресованы учителям, работающим по учебнику «Геометрия. 7 класс» (авторы А.Г. Мерзляк В.Б. Полонский, М.С. Якир), но могут быть использованы и учителями, работающими по другим учебникам.
- Просмотр содержимого документа «Математические диктанты по геометрии, 7 класс»
- Математические диктанты по геометрии, 7 класс материал (геометрия, 7 класс) по теме
- Скачать:
- Предварительный просмотр:
- Акмолинская область
- Бурабайский район
- СШ №3 им.П.И.Морозова
- Дидактический материал
- Математические диктанты
- геометрия, 7 класс
- Автор: Гуранская Г.В . учитель математики и информатики
- г.Щучинск
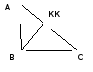
- Признаки равенства треугольников
- Признаки параллельности прямых
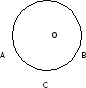
- Окружность
- 1. Геометрическая фигура, состоящая из множества всех точек, равноудаленных от данной точки?
- 2. Хорда, проходящая через центр окружности?
- 3. Отрезок, соединяющий центр окружности с точкой на окружности?
- 4. Пересекаются ли окружности с центрами А и В, если АВ = 10 см, а радиусы равны 5 см, и 6 см?
- 5. Расстояние от центра окружности до точки А равно d, а радиус окружности равен r. Сравните d и r, если точка А лежит вне круга, ограниченного данной окружностью?
- 6. Расстояние от центра окружности до точки В равно m, а радиус окружности равен r. Сравните m и r, если точка B лежит внутри круга, ограниченного данной окружностью?
- По теме: методические разработки, презентации и конспекты
- Математические диктанты по геометрии. Тема:»Начальные геометрические сведения» и »Треугольники»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
Просмотр содержимого документа
«Математические диктанты по геометрии, 7 класс»
Математические диктанты по геометрии
(7 класс, учебник авт. А.Г.Мерзляк, В.Б.Полонский, М.С.Якир)
Диктант 1 по теме «Точки и прямые. Отрезок и его длина»
Сколько прямых можно провести через заданную точку?
Сколько прямых можно провести через три точки, лежащие на одной прямой?
Сколько прямых задают четыре точки, никакие три из которых не лежат на одной прямой?
Как называют утверждение, разъясняющее смысл какого-то термина (понятия)?
Сколько общих точек имеют две пересекающиеся прямые?
Какая фигура определяется однозначно любыми двумя своими точками?
Как называют точку, принадлежащую отрезку, но не совпадающую с его концами?
Запишите, что длина отрезка АВ больше длины отрезка СD.
Длина отрезка АВ в два раза больше длины отрезка СD. Чему равна длина отрезка СD, если отрезок АВ – единичный?
Диктант 2 по теме «Луч. Угол. Измерение углов»
Каково другое название луча?
На прямой отметили три точки. Сколько при этом образовалось лучей?
Как называют лучи, имеющие общее начало, объединением которых является прямая?
На сколько углов делят плоскость два луча, имеющие общее начало?
Как с помощью одной буквы обозначить угол АМС?
Как называют угол, стороны которого являются дополнительными лучами?
Переведите в градусы 312.
Переведите в минуты 0,4.
Какой угол можно разделить лучом, выходящим из его вершины, на острый и прямой углы?
Диктант 3 по теме «Смежные и вертикальные углы»
Какова градусная мера угла, смежного с углом 42?
Какова градусная мера угла, вертикального углу 156?
Нарисуйте два угла, имеющие общую сторону, но не являющиеся смежными.
Нарисуйте два равных невертикальных угла так, чтобы сторона одного угла являлась дополнительным лучом к стороне другого угла.
Сколько существует углов, смежных с данным?
Сколько существует углов, вертикальных с данным?
Для данного угла построили смежный и вертикальный с ним углы. Оказалась, что градусные меры построенных углов равны. Найдите градусную меру данного угла.
Сумма двух углов, образованных при пересечении двух прямых, равна 180. Обязательно ли эти углы будут смежными?
Диктант 4 по теме «Перпендикулярные прямые»
Сколько прямых углов может образоваться при пересечении двух прямых?
При пересечении двух прямых образовался угол, равный 73. Чему равен угол между этими прямыми?
При пересечении двух прямых образовался угол, равный 91. Чему равен угол между этими прямыми?
Нарисуйте отрезок и перпендикулярную ему прямую так, чтобы они не имели общих точек.
Нарисуйте луч и перпендикулярный ему отрезок так, чтобы один из концов отрезка принадлежал лучу.
Точки А и В равноудалены от прямой a. Может ли отрезок АВ пересекать прямую a? Ответ проиллюстрируйте рисунком.
Нарисуйте перпендикулярные прямые a и b. На прямой b отметьте все точки, которые удалены от прямой a на 2 см.
Сколько можно провести наклонных из данной точки к данной прямой?
Диктант 5 по теме «Треугольники. Равные треугольники»
Какой угол противолежит стороне MN в треугольнике MNP?
Какая сторона противолежит углу F в треугольнике EKF?
Какие углы прилежат к стороне CD в треугольнике CKD?
Как может называться треугольник, в котором нет тупого угла?
Нарисуйте треугольник АВС. На стороне АС треугольника АВС отметьте точки М и N так, чтобы треугольники АВС и МВN имели общую медиану.
Нарисуйте треугольник АВС. На стороне АС треугольника АВС отметьте точки М и N так, чтобы треугольники АВС и МВN имели общую биссектрису.
Нарисуйте треугольник АВС. На стороне АС треугольника АВС отметили точку М и провели отрезок ВМ. Назовите все треугольники, имеющие общую высоту.
Биссектриса ВК треугольника АВС образовала со стороной АВ угол, величина которого равна 47. Определите вид треугольника АВС.
Отрезок АМ – медиана треугольника АВС. Разность периметров треугольников АМС и АМВ равна 8 см. Найдите АС – АВ.
Диктант 6 по теме «Первый и второй признаки равенства треугольников»
1. Две стороны одного треугольника равны двум сторонам другого треугольника, но сами треугольники не равны. Что можно сказать об углах между этими сторонами?
2. Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то равны ли такие треугольники? Свой ответ подтвердите рисунком.
3. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то равны ли такие треугольники? Свой ответ подтвердите рисунком.
4. Треугольники АВС и MNK равны. Может ли сторона АВ не быть равной стороне MN? Свой ответ подтвердите рисунком.
5. Треугольники АВС и MNK не равны. Известно, что А = М, В = N. Что можно сказать о сторонах АВ и MN?
6. Если сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то равны ли такие треугольники? Свой ответ подтвердите рисунком.
7. Сколько серединных перпендикуляров имеет данный отрезок?
Диктант 7 по теме «Свойства и признаки равнобедренного треугольника»
В равнобедренном треугольнике АВС (АВ = ВС) проведена биссектриса ВК. Найдите угол ВКС.
В равнобедренном треугольнике ЕFК отрезки EF и FK являются боковыми сторонами. Укажите равные углы треугольника ЕFК.
В равнобедренном треугольнике MNK отрезок МК – основание. Укажите равные углы треугольника MNK.
На основании какого свойства равнобедренного треугольника можно доказать, что медиана равнобедренного треугольника, проведенная к его основанию, принадлежит серединному перпендикуляру основания?
На основании какого свойства равнобедренного треугольника можно доказать, что каждая точка биссектрисы равнобедренного треугольника, проведенной к его основанию, равноудалена от вершин углов при основании?
В треугольнике АВС биссектриса и медиана, проведенные из вершины А, совпадают. Также совпадают биссектриса и медиана, проведенные из вершины В. Докажите, что биссектриса и медиана, проведенные из вершины С, также совпадают.
Определите вид треугольника, в котором ни одна высота не совпадает ни с одной медианой.
Дан отрезок АВ. Какую фигуру образуют все такие точки Х, что треугольник АХВ – равнобедренный с основанием АВ?
Диктант 8 по теме «Признаки и свойства параллельных прямых»
Нарисуйте два луча, не имеющие общих точек и не являющиеся параллельными.
Прямая a перпендикулярна прямой b, прямая b перпендикулярна прямой с. Каково взаимное расположение прямых a и с?
Прямые a и b параллельны. Прямая с не имеет общих точек с прямой b. Каково взаимное расположение прямых a и с?
Любая прямая, проходящая через точку М, пересекает прямую АВ. Каково взаимное расположение точки М и прямой АВ?
Точка М принадлежит прямой АВ, но не принадлежит лучу АВ. Сколько лучей, параллельных лучу АВ, можно провести через точку М?
Точка М не принадлежит прямой АВ. Сколько лучей, параллельных лучу АВ, можно провести через точку М?
Гарантирует ли данное условие параллельность прямых a и b.
Гарантирует ли данное условие параллельность прямых a и b.
1) 1 + 3 = 180 и 6 + 8 = 180;
9. Сумма двух соответственных углов при двух параллельных прямых и секущей равна 180. Найдите эти углы.
10. Точки М и N лежат соответственно на двух параллельных прямых a и b. Расстояние от точки М до прямой b равно 10 см. Найдите расстояние от точки N до прямой a.
Диктант 9 по теме «Сумма углов треугольника»
Определите вид треугольника, если два его угла равны:
Найдите углы прямоугольного треугольника, в котором один из острых углов в два раза больше другого острого угла.
Найдите углы при основании равнобедренного треугольника, если угол при вершине равен 40.
Найдите угол между боковой стороной равнобедренного треугольника и медианой, проведенной к основанию, если угол при основании равнобедренного треугольника равен 50.
В равнобедренном треугольнике медиана, проведенная к основанию, равна его половине. Найдите углы равнобедренного треугольника.
Внешние углы треугольника АВС при вершинах А и С равны по 100. Какова величина внешнего угла при вершине В?
Сумма внешних углов при вершинах А и В треугольника АВС равна 270. Определите вид треугольника АВС.
Две стороны равнобедренного треугольника равны 4 см и 9 см. Найдите третью сторону треугольника.
В треугольнике АВС известно, что А = 29, В = 81. Запишите стороны треугольника АВС в порядке возрастания их длин.
Диктант 10 по теме «Прямоугольный треугольник и его свойства»
Стороны прямоугольного треугольника равны 5 см, 12 см, 13 см. Найдите гипотенузу этого треугольника.
Высота равнобедренного прямоугольного треугольника, проведенная к гипотенузе, равна 10 см. Найдите гипотенузу этого треугольника.
В прямоугольном треугольнике АВС гипотенуза АВ равна 8 см. Внешний угол при вершине А равен 150. Найдите катет ВС.
В равнобедренном треугольнике высота, проведенная из вершины, в два раза меньше боковой стороны. Найдите углы равнобедренного треугольника.
Верно ли, что если катет и острый угол одного прямоугольного треугольника равны катету и острому углу другого, то такие треугольники равны? Свой ответ проиллюстрируйте рисунком.
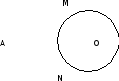
Диктант 11 по теме «Геометрическое место точек, окружность и ее свойства»
Какой фигурой является ГМТ, принадлежащих углу и удаленных от его вершины на 3 см?
Укажите ГМТ, равноудаленных от вершин данного треугольника.
Укажите ГМТ, равноудаленных от сторон данного треугольника.
В каком отношении делит диаметр хорду, которой он перпендикулярен?
Диаметр АВ пересекает хорду CD, отличную от диаметра, в ее середине. Найдите угол между прямыми АВ и CD.
Хорда АВ окружности с центром в точке О равна радиусу этой окружности. Найдите угол ОАВ.
Хорда АВ окружности перпендикулярна радиусу ОС и делит его пополам. Найдите угол ОАВ.
Две прямые касаются окружности в точках А и В, где А и В – концы диаметра. Каково взаимное расположение этих касательных?
Из точки А к окружности с центром О проведены две касательные АМ и АN, М и N – точки касания. Известно, что МОN = 100. Найдите МАО.
Укажите точку, в которой пересекаются серединные перпендикуляры катетов прямоугольного треугольника.
Видео:Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Математические диктанты по геометрии, 7 класс
материал (геометрия, 7 класс) по теме
Брошюра содержит диктанты по всем темам курса геометрии 7 класса
Видео:Сумма углов треугольника. Геометрия 7 класс | МатематикаСкачать

Скачать:
| Вложение | Размер |
|---|---|
| diktanty_po_geometrii_7_klass.rar | 143.54 КБ |
Видео:Бестселлер Все правила по геометрии за 7 классСкачать

Предварительный просмотр:
Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Акмолинская область
Видео:Математика это не ИсламСкачать

Бурабайский район
Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

СШ №3 им.П.И.Морозова
Видео:Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Дидактический материал
Видео:Треугольники. 7 класс.Скачать

Математические диктанты
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

геометрия, 7 класс
Видео:Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

Автор: Гуранская Г.В . учитель математики и информатики
Видео:Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

г.Щучинск
Данный материал предназначен для учителей математики, который можно применять как для промежуточного контроля усвоения темы, так и для итогового контроля при завершении изученного раздела и отдельной темы.
Контроль знаний имеет обучающее и воспитывающее значение, способствует более глубокому изучению учащимися основ наук, совершенствованию их знаний и умений.
Математические диктанты — хорошо известная форма контроля знаний. Учитель сам или с помощью звукозаписи задает вопросы, учащиеся записывают под номерами краткие ответы на них. Как правило, ребятам трудно воспринимать задания на слух. Но если диктанты проводить часто, то школьники овладевают этим навыком. А ценность такого умения неоспорима. Иногда слуховому восприятию нужно помочь. Для этого одновременно с чтением задания делаю запись или чертеж на доске. В зависимости от подготовленности учащихся число заданий увеличиваю или уменьшаю.
Опрос у доски обычно дополняют так называемым устным счетом. Недостаток традиционного «устного счета» в том, что в нем участвуют не все ученики. Альтернатива опроса и «устного счета» — математический диктант. Отсюда — его место в учебном процессе: в начале урока, на котором начинается изложение новой порции знаний. Или в конце урока на этапе рефлексии. Отсюда — требование к его содержанию: ответы на вопросы должны показывать, усвоено ли содержание ранее изложенного материала. Математический диктант может заменить опрос по теме, заданной для повторения. Его продолжительность обычно 10–15 минут.
Математический диктант — это один из способов организации самостоятельной деятельности учащихся. Система математических диктантов, с одной стороны, должна обеспечивать усвоение необходимых знаний и умений, с другой стороны, их проверку.
Математические диктанты можно разделить на следующие виды: проверочные, обзорные, итоговые. Каждый вид математических диктантов имеет свои особенности, свои цели, и следовательно, требования, предъявляемые к составлению этих работ, должны быть различны.
Проверочные диктанты предназначены для контроля усвоения отдельного фрагмента курса в период изучения темы. Поскольку проверочные диктанты проводятся после отработки основных умений и навыков, то в них включаются задания не только репродуктивного характера. (Задания репродуктивного типа выполняются учащимися на основе известных формул и теорем, определений, свойств тех или иных математических объектов.) Основа проверочных диктантов — задания реконструктивного характера. ( Реконструктивные задания указывают только на общий принцип решений или на соотнесение к тому или иному материалу (например, «решите задачу составлением системы уравнений»). Выполнение таких заданий возможно только после того, как ученик сам реконструирует их, соотнесет с несколькими репродуктивными.)
Обзорный диктант проводится после завершения изучения раздела когда целесообразно проверить его усвоение в целом. Диктант позволит учащимся повторить материал, систематизировать знания, установить связи между изученными вопросами. Задания должны быть четкими, конкретными, понятными. Сюда входят вопросы по проверке изученных определений, теорем, правил, задания на решение несложных задач и упражнений.
Итоговые диктанты проводятся для повторения в конце года по основным содержательным линиям изученного курса. В них следует включать задания, которые должны проверять основные умения и навыки; задания на повторение основных теоретических вопросов: воспроизведение определений и свойств математических объектов.
При чтении заданий диктанта паузы определяются по темпу работы среднего ученика. Наблюдения показали, что достаточна пауза, равная времени повтора текста. Следует помнить, что математический диктант проверяет не сообразительность учащихся, а их знания. И если учащийся при ответе на вопрос диктанта надолго задумался, он просто не знает ответ, и долгая пауза ему не поможет.
Точка, прямая, отрезок
- Часть прямой ограниченная двумя точками.
- Точки, ограничивающие отрезок.
- Как называются два отрезка, которые имеют только одну общую точку?
- Сколько прямых можно провести через две точки?
- Как обозначаются точки и прямые?
- Дана прямая а . Отметьте точки А, В и С, чтобы прямые АВ и а пересекались в точки С, лежащей между точками А и В.
- Постройте отрезок АС и измерьте его длину.
- Какой фигурой является центр окружности?
- Какой фигурой является диаметр окружности?
- Фигура, образованная двумя лучами, выходящими из одной точки.
- Часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной точки.
- Как обозначается угол?
- Утверждение, принимаемое без доказательства и определяющее основные свойства простейших геометрических фигур.
- Утверждение, которое необходимо доказывать.
- Рассуждение, с помощью которого устанавливается правильность утверждения о свойстве геометрической фигуры.
- Единица измерения углов.
- Сколько неразвернутых углов образуется при пересечении двух прямых?
- Инструмент для измерения углов.
- Построить угол заданной градусной меры (например, 75°).
Смежные и вертикальные углы
- Угол меньше 90°.
- Угол равный 90°.
- Градусная мера развернутого угла.
- Чему равна треть прямого угла?
- Прямой угол разделен на два угла, один из которых равен 40°? Чему равен второй угол?
- Развернутый угол разделен на два угла, один из которых равен 100°? Чему равен второй угол?
- На какой угол поворачивается солдат по команде “кругом”?
- Развернутый угол разделен на два угла, один из которых равен 50°? Чему равен второй угол?
- Два угла, у которых одна сторона общая, а две другие являются дополнительными лучами.
- Если стороны одного угла являются дополнительными лучами сторон другого угла, то такие углы называются …
- Угол больше 90°, но меньше 180°.
- Свойство смежных углов.
- Свойство вертикальных углов.
- Луч, исходящий из вершины угла и делящий его на два равных угла.
- Обозначение перпендикулярности прямых.
- Постройте треугольник. Обозначьте вершины треугольника. Запишите: стороны треугольника, углы треугольника.
- Какие треугольники называются равными?
- В равных треугольниках против соответственно равных сторон лежат …
- Сумма длин всех сторон треугольника.
- Что означает выражение ∆ АВС = ∆ А 1 В 1 С 1 ?
- Постройте треугольники ∆ АВС ∆ КОМ так, чтобы АВ║ КМ.
- Постройте треугольник и найдите его периметр.
Высота, биссектриса и медиана треугольника
- Перпендикуляр, проведенный из данной вершины к прямой, проходящей через противоположную сторону треугольника.
- Отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне.
- Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны треугольника.
- Какой треугольник называется равнобедренным?
- Какой треугольник называется равносторонним?
- Свойство равнобедренного треугольника.
- Постройте тупоугольный треугольник. Проведите все его высоты.
- Начертите равнобедренный прямоугольный треугольник.
- В ∆ АВС АВ=ВС. АВ = 3см, АС = 2см. Найти периметр треугольника.
- Начертите равнобедренный треугольник. Постройте высоту, медиану и биссектрису к основанию треугольника. Сделайте вывод.
Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Признаки равенства треугольников
Для проведения данного диктанта используется интерактивная доска или проектор.
1. В ∆ABC и ∆DEF АВ = DЕ, A = D, BC = EF. Равны ли эти треугольники по первому признаку?
1. В ∆ABD и ∆MPQ АВ = MP, А = M, AD = MQ. Равны ли эти треугольники по первому признаку?
2. В ∆KNM и ∆PQT KN = PQ, N =Q. Какое ещё условие должно быть выполнено, чтобы треугольники были равны по первому признаку?
2. В ∆ABС и ∆DEF А = D, AC = DF. Какое ещё условие должно быть выполнено, чтобы треугольники были равны по первому признаку?
3. В ∆ABC и ∆DFQ АВ = DF, А =D, В =F. Равны ли эти треугольники по второму признаку?
3. В ∆ABD и ∆MPQ АВ = MP, А =M, В =P. Равны ли эти треугольники по второму признаку?
4. В ∆KNM и ∆PQT KN = PQ, N =Q. Какое ещё условие должно быть выполнено, чтобы треугольники были равны по второму признаку?
4. В ∆ABC и ∆DEF А =D, C =F. Какое ещё условие должно быть выполнено, чтобы треугольники были равны по второму признаку?
5. В ∆ABC и ∆DFQ АВ = DЕ, BC = FQ, AC = DQ. Равны ли эти треугольники по третьему признаку?
5. В ∆ABD и ∆MPQ АВ = MP, AD = MQ, BD = PQ. Равны ли эти треугольники по третьему признаку?
6. Сколько условий должно выполняться, чтобы треугольники были равны по первому признаку? Какие это условия?
6. Сколько условий должно выполняться, чтобы треугольники были равны по второму признаку? Какие это условия?
7. Продолжите предложение: «Второй признак равенства треугольников – это признак равенства по …….»
7. Продолжите предложение: «Третий признак равенства треугольников – это признак равенства по …….»
8. Докажите равенство ∆АВС и ∆МКС.
8. Докажите равенство ∆АВС и ∆МВК.
9. Посмотрите на рисунок. Можно ли воспользоваться для установления равенства треугольников одним из признаков равенства?
9. Посмотрите на рисунок. Можно ли воспользоваться для установления равенства треугольников одним из признаков равенства?
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Признаки параллельности прямых
- Две прямые на плоскости называются параллельными, если …
- Прямая называется секущей, если …
- Внутренними накрест лежащими углами при пересечении двух прямых a и b секущей c (см. рис.) являются углы …
Внешними односторонними являются углы …
- Признак параллельности двух прямых заключается в следующем: …
- Если две прямые параллельны третьей, то …
- Две прямые на плоскости называются не параллельными, если …
- Параллельность прямых обозначается …
- Внешними накрест лежащими углами при пересечении двух прямых a и b секущей c (см. рис.) являются углы …
Внутренними односторонними являются углы …
- Аксиома параллельных прямых заключается в следующем: …
- Если две прямые параллельны третьей, то …
Сумма углов треугольника
Закончи предложение или вычеркни лишнюю информацию.
- Сумма углов треугольника равна …
- Если углы равнобедренного треугольника при основании равны по 50 о , то угол между боковыми сторонами равен…
- Углы равностороннего треугольника равны по…
- Внешним углом треугольника при данной вершине называется…
- Сумма внешнего и внутреннего углов треугольника при данной вершине равна…
- В ∆ КМА внешним является угол…
- Если два внешних угла ∆ АВС равны 100 о и 140 о , то третий внешний угол равен…
- Сумма углов треугольника равна …
- Если в ∆ АВС А = 35 о , B = 55 о , то С =…
- Если угол между боковыми сторонами равнобедренного треугольника равен 100 о , то углы при основании равны по…
- Если сумма двух углов треугольника равна третьему углу, то этот треугольник … ( вид треугольника) .
- При данной вершине можно построить … внешних углов.
- Внешний угол треугольника равен…
- В КМА внешний МАС >…
- Если один из углов треугольника прямой, то треугольник называется …
- Сумма острых углов прямоугольного треугольника равна …
- Сторона треугольника, лежащая против прямого угла, называется …
- Стороны треугольник, прилежащие к прямому углу называются …
- Катет, лежащий против угла в 30 о , равен …
Соотношения между сторонами и углами треугольника
- В ∆ АВС АВ = 10см, ВС = 11см. Сравните углы С и А.
- В равнобедренном треугольнике угол при основании равен 20 о . Чему равен угол при вершине треугольника?
- В ∆ АВС А=40 о , С=41 о . Сравните стороны треугольника ВС и АВ.
- Даны прямоугольные треугольники. По данным рисунка найдите разность NF-N 1 F 1 .
- В ∆ EFK E= K, FM ┴ EK. Сравните EFM и MFK.
- В ∆ АВС А=30 о , В=100 о . Тогда внешний угол при вершине С равен …
- В ∆ АВС А= С. ВD – медиана. Найти BDC.
На рисунке даны прямоугольные треугольники. По данным рисунка найдите отношение АС /А 1 С 1 .
Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Окружность
Видео:7 класс, 14 урок, ТреугольникСкачать

1. Геометрическая фигура, состоящая из множества всех точек, равноудаленных от данной точки?
Видео:ВСЕ ВИДЫ ТРЕУГОЛЬНИКОВ😉 #егэ #огэ #математика #профильныйегэ #shorts #геометрия #образованиеСкачать

2. Хорда, проходящая через центр окружности?
Видео:Миникурс по геометрии. ТреугольникиСкачать

3. Отрезок, соединяющий центр окружности с точкой на окружности?
Видео:Решали пол-урока, а оказалось очень простоСкачать

4. Пересекаются ли окружности с центрами А и В, если АВ = 10 см, а радиусы равны 5 см, и 6 см?
Видео:ТреугольникСкачать

5. Расстояние от центра окружности до точки А равно d, а радиус окружности равен r. Сравните d и r, если точка А лежит вне круга, ограниченного данной окружностью?
Видео:Геометрия. 7 класс. Теоремы. Т5. Первое свойство равнобедренного треугольника.Скачать

6. Расстояние от центра окружности до точки В равно m, а радиус окружности равен r. Сравните m и r, если точка B лежит внутри круга, ограниченного данной окружностью?
По теме: методические разработки, презентации и конспекты
математический диктант по геометрии 9 класс по теме:» Многоугольник.»
Математический диктант по теме «Многоугольник» для 9 класса.
Математический диктант. Площади.Геометрия 8 класс.
Математический диктант-одна из форм быстрой проверки знаний и умений учащихся.
Математический диктант по геометрии 11 класс «Простейшие задачи в координатах»
Математический диктант по теме «Простейшие задачи в координатах» разработан для учащихся 11 классов, изучающих геометрию по учебнику «Геометрия 10-11 классы» автора Л.С. Атанасян.Данная работа п.
Математические диктанты по геометрии для 8 класса (12.01.2016)
Математические диктанты по геометрии для 8 класса по учебнику Л.С.Атанасяна.
Математические диктанты по геометрии для 10 класса (28.02.2016)
Матемактические диктанты по геометрии для 10 класса.
7 класс. Математические диктанты по геометрии
7 класс. Математические диктанты по геометрии.
9 класс. Математические диктанты по геометрии.
9 класс. Математические диктанты по геометрии.
Математические диктанты по геометрии. Тема:»Начальные геометрические сведения» и »Треугольники»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Геометрия 7 класс. По учебнику Л.С.Атанасяна, В.Ф.Бутузова (главы1,2)
1глава. Начальные геометрические сведения
Тема: Прямая и отрезок. Луч и угол.
1. Проведите прямую а , и отметьте точки А, В и С, лежащие на прямой а и точки К, М, Е не лежащие на прямой а .
2. Начертите прямую а , отметьте на ней точки А и В. Отметьте точку М лежащую на прямой а , но не принадлежащую отрезку АВ.
3.Могут ли две прямые иметь две общих точки?
4. Закончите предложение: Угол называется развернутым, если его стороны…
5. Начертите луч АВ и луч АК. Какую фигуру вы получили?
6. Верно ли что: Любая часть прямой — это отрезок?
7. На прямой отмечены четыре точки А, В, С и К. Сколько отрезков получилось?
8. На прямой отметили три точки. Сколько лучей получилось?
9. Закончите предложение: Через любые две точки…
10. Из одной точки провели четыре луча. Сколько углов получилось?
Тема: Измерение отрезков и углов
1. Начертите тупой угол и измерьте его.
2. Верно ли что: тупой угол — это угол, градусная мера которого больше 90°
3. Определите вид угла, если его градусная мера равна 89°.
4. Закончите предложение: Две геометрические фигуры называются равными…
5. Верно ли, что: Луч, исходящий из вершины угла и делящий этот угол на два угла называется биссектрисой угла?
6. Луч ОК – биссектриса угла АОВ. Угол АОК равен 56°. Найдите градусную меру угла АОВ
7. Точка В делит отрезок АС на два отрезка. Найдите отрезок АС, если АВ = 5,6см, ВС= 4,3
8. Точка С – середина отрезка АВ, Точка К – середина отрезка СВ. Найдите длину отрезка АК, если АВ = 12см
9. Закончите предложение: Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называется…
10. Луч ОЕ делит угол АОВ на два угла. Найдите угол АОВ, если угол АОЕ равен 54°, а угол ЕОВ равен 65°
Математический диктант №3
Тема: Перпендикулярые прямые. Смежные и вертикальные углы
1. Начертите острый угол АВС. Начертите смежный с ним угол.
2. Найдите угол смежный с углом АВС, если угол АВС равен 112°
3. Верно ли утверждение: если смежные углы равны, то они прямые?
4. Закончите предложение: Вертикальные углы…
5. Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма трех углов равна 250°
6. Закончите предложение: Две пересекающиеся прямые называются перпендикулярными…
7. Верно ли что: Две прямые перпендикулярные третьей, не пересекаются?
8. Может ли при пересечении двух прямых сумма трех углов быть 180°
9. Верно ли что: два угла называются смежными, если стороны одного угла являются продолжениями сторон другого?
10. Один из смежных углов тупой. Каким является другой угол?
2 глава. Треугольники
Математический диктант №4
Тема: Признаки равенства треугольников
1.Верно ли утверждение: Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны
2.Закончите предложение: Теорема – это…
3.В треугольниках АВС и МКН: АВ=МК, угол А равен углу М, угол В равен углу К. АС=9см. ВС=7см. Найдите МН.
4.Верно ли утверждение: Если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники равны?
5.В треугольниках АВС и КМЕ: АВ=КМ, ВС=МЕ, АС=КЕ. Угол А равен 45°, угол В=100°. Найдите градусную меру угла М
6. Верно ли утверждение: Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны?
7. Закончите предложение: В равных треугольниках против соответственно равных сторон…
8. Отрезки АВ и СМ пересекаются в точке О. АО=ОВ, СО=ОМ. АС=6см, АВ=9см. Найдите ВМ.
9. Верно ли , что два любых прямоугольных треугольника равны?
10. Запишите формулировку второго признака равенства треугольников.
Математический диктант № 5
Тема: Равнобедренный треугольник. Медианы, биссектрисы и высоты треугольника
1. Закончите предложение: Треугольник, у которого две стороны равны называется…
2. В равнобедренном треугольнике АС-основание. АВ=6см, АС=4см. Найдите периметр треугольника АВС.
3.Треугольник АВС – равнобедренный, АВ=ВС. Угол С равен 34°. Найдите угол А.
4. Верно ли что: Медиана треугольника – это отрезок, соединяющий вершину треугольника с противоположной стороной?
5. Верно ли что: В любом треугольнике высоты пересекаются в одной точке?
6. Периметр равностороннего треугольника равен 24см. Найдите сторону этого треугольника.
7. Закончите предложение: В равнобедренном треугольнике, биссектриса, проведенная к основанию…
8. Начертите остроугольный треугольник АВС. Проведите его высоты с помощью чертежного угольника
9. Треугольник АВС – равнобедренный . АС – основание . ВМ – медиана .
ВМ=4см. Периметр треугольника АВС равен 16см. Найдите периметр треугольника АВМ
10. Закончите предложение: Равные стороны равнобедренного треугольника называются…
1. Постройте окружность с центром в точке О и диаметром 6см.
2. Любые две точки окружности делят окружность на две части. Как называют эти части?
3. Закончите предложение: Диаметр окружности – это…
4. Верно ли утверждение: Хорда окружности является ее диаметром
5. АВ – хорда окружности, с центром в точке О. Отрезок ОА равен 5см, найдите длину отрезка ОВ.
6. АВ и МК диаметры окружности с центром в точке О. АМ = 7см. Найдите КВ.
7.Радиус окружности равен17мм. Найдите диаметр окружности.
8. АВ и МК диаметры окружности с центром в точке О. АВ = 10см, АМ =6см. Найдите периметр треугольника АМО.
9. АВ – хорда окружности, с центром в точке О. угол АВО равен 40°, найдите градусную меру угла ВАО.
10. Закончите предложение: Круг – это….
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 1009 человек из 78 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 311 человек из 70 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 678 человек из 74 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 549 475 материалов в базе
Другие материалы
- 18.02.2016
- 339
- 0
- 18.02.2016
- 756
- 0
- 18.02.2016
- 536
- 0
- 18.02.2016
- 378
- 0
- 18.02.2016
- 21244
- 1353
- 18.02.2016
- 581
- 0
- 18.02.2016
- 495
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 18.02.2016 11003
- DOCX 19.6 кбайт
- 174 скачивания
- Рейтинг: 4 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Попова Ольга Алексеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет
- Подписчики: 0
- Всего просмотров: 25802
- Всего материалов: 6
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минобрнауки подготовит государственный рейтинг университетов
Время чтения: 1 минута
В Омской области школы и колледжи перейдут на дистанционное обучение с 7 по 21 февраля
Время чтения: 1 минута
У 76% российских учителей оклад ниже МРОТ
Время чтения: 2 минуты
Петербургская учительница уволилась после чтения на уроке Введенского и Хармса
Время чтения: 3 минуты
Полный перевод школ на дистанционное обучение не планируется
Время чтения: 1 минута
В Самаре и Тольятти часть школьников перевели на дистанционное обучение
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.