Как найти радиан на окружности

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Видео:Тригонометрическая окружность. Как выучить?Скачать

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Видео:Как искать точки на тригонометрической окружности.Скачать

Перевод градусов в радианы и обратно: формулы, примеры

Углы измеряются в градусах или в радианах. Важно понимать связь между этими единицами измерения. Понимание этой связи позволяет оперировать углами и осуществлять переход от градусов к радианам и обратно. В данной статье выведем формулу для перевода градусов в радианы и радианов в градусы, а также разберем несколько примеров из практики.

Видео:Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

Связь между градусами и радианами

Чтобы установить связь между градусами и радианами, необходимо узнать градусную и радианную меру какого-либо угла. Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла необходимо длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π · r . Разделим длину дуги на радиус и получим радианную меру угла: π · r r = π рад.

Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180 ° . Следовательно 180 ° = π рад.

Связь градусов с радианами

Связь между радианами и градусами выражается формулой

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Формулы перевода радианов в градусы и наоборот

Из формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и из градуов в радианы.

Выразим один радиан в градусах. Для этого разделим левую и правую части радиуса на пи.

1 р а д = 180 π ° — градусная мера угла в 1 радиан равна 180 π .

Также можно выразить один градус в радианах.

1 ° = π 180 р а д

Можно произвести приблизтельные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.

1 р а д = 180 π ° = 180 3 , 1416 ° = 57 , 2956 °

Значит, в одном радиане примерно 57 градусов

1 ° = π 180 р а д = 3 , 1416 180 р а д = 0 , 0175 р а д

Один градус содержит 0,0175 радиана.

Формула перевода радианов в градусы

x р а д = х · 180 π °

Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.

Видео:Радианная мера угла. 9 класс.Скачать

Примеры перевода градусов в радианы и радианов в градусы

Пример 1. Перевод из радианов в градусы

Пусть α = 3 , 2 рад. Нужно узнать градусную меру этого угла.

Применим формулу перехода от радианов к градусам и получим:

3 , 2 р а д = 3 , 2 · 180 π ° ≈ 3 , 2 · 180 3 , 14 ° ≈ 576 3 , 14 ° ≈ 183 , 4 °

Аналогично можно получить формулу перевода из градусов в радианы.

Формула перевода из градусов в радианы

y ° = y · π 180 р а д

Переведем 47 градусов в радианы.

Согласно формуле, умножим 47 на пи и разделим на 180.

Видео:Угловая скорость и радианная мера углаСкачать

Тригонометрия простыми словами

Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».

Тригонометрические функции связаны с соотношениями сторон в прямоугольном треугольнике:

• Синус угла – отношение противолежащего катета к гипотенузе;
• Косинус угла – отношение прилежащего катета к гипотенузе;
• Тангенс угла – отношение противолежащего катета к прилежащему;
• Котангенс угла – отношение прилежащего катета к противолежащему.

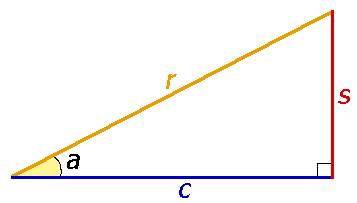
Или в виде формул:

Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).

Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.

Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.

Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.

Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.

Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.

Значения тригонометрических функций
для первой четверти круга (0° – 90°)

0°	30°	45°	60°	90°
sin	0	1	√3	–
ctg	–	√3	1	Принцип повтора знаков тригонометрических функций Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону. В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ. Например, значения тригонометрических функций для углов 270° и -90° равны. Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно. Видео:Что такое радиан?Скачать Тригонометрический круг Углы в радианах Для математических вычислений тригонометрических функций используются углы не в градусах, а в радианах. Что такое радиан? Угол в радианах равен отношению длины дуги окружности к радиусу. Полный круг в 360° соответствует длине окружности 2 π r. Следовательно 360° в радианах равно 2 π , а 180° равно π радиан. Как преобразовывать градусы в радианы? Нужно значение в градусах разделить на 180° и умножить на π . Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций. 🔥 Видео ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать Алгебра 10 класс (Урок№29 - Радианная мера угла.)Скачать Длина окружности. Математика 6 класс.Скачать Перевод радиан в градусы (видео 12) |Окружность и Круг | ГеометрияСкачать 4. Как найти точки на тригонометрической окружности. Положительные углы в радианах.Скачать 5. Как найти точки на тригонометрической окружности. Отрицательные углы в градусах и радианах.Скачать Всё про углы в окружности. Геометрия | МатематикаСкачать Как найти центр и радиус нарисованной окружности #математика #егэ2023 #школа #fyp #shortsСкачать Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать Откуда в окружности 2 Пи радиан?Скачать Длина дуги окружности. 9 класс.Скачать Как запомнить тригонометрический круг специально ничего не выучивая?Скачать Длина окружности. Площадь круга - математика 6 классСкачать Поделиться или сохранить к себе: Смотрите также Ящик тянут по земле по горизонтальной окружности длиной 60 Ящик тянут по земле по горизонтальной окружности длиной 40 Ящик тянут по земле по горизонтальной окружности диаметром 20 Ящик тянут по земле за веревку по горизонтальной окружности длиной Ящик тянут по земле за веревку по горизонтальной окружности диаметром Электрон равномерно движется по окружности в однородном магнитном поле Электрон и протон ускоренные разностью потенциалов движутся по окружности Шарик скатывается по желобу изогнутому в виде дуги окружности