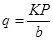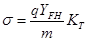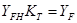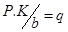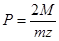Диаметры окружностей вершин цилиндрического колеса (2 видео)

Глава 8. зацепления зубчатые

Содержание

Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.
Расчет основных геометрических параметров цилиндрических прямозубых колес
Выполнение эскиза зубчатого колеса
Определение модуля и числа зубьев
Подсчет основных параметров зубчатого колеса
Выполнение эскиза
Особенности чертежей цилиндрических колес с косыми зубьями
🎬 Видео

Видео:Модуль шестерни и параметры зубчатого колесаСкачать

Зацепления зубчатые относятся к передачам (подвижным соединениям) и передают движение от двигателя к исполнительным механизмам. К составным частям зубчатых передач относятся зубчатые колеса (цилиндрические, конические), червяки, рейки.

Диаметр делительной окружности d является одним из основных параметров, по которому производят расчет зубчатого колеса:

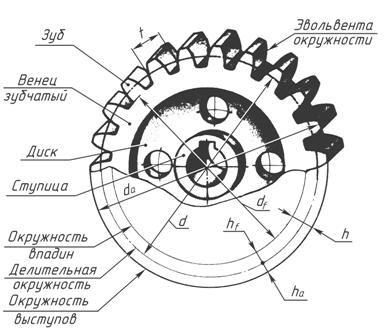
где z – число зубьев;

Модуль зацепления m – это часть диаметра делительной окружности, приходящейся на один зуб:

где t – шаг зацепления.

где h _a – высота головки зуба, h _a = m ; h _f – высота ножки зуба, h _f = 1,25 m .

Диаметр окружности выступов зубьев :

Диаметр окружности впадин :

Служит для передачи вращения при параллельных осях валов.

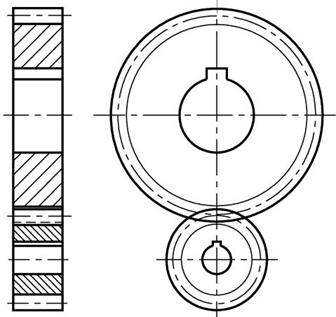
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2 .

Служит для преобразования вращательного движения в возвратно-поступательное.

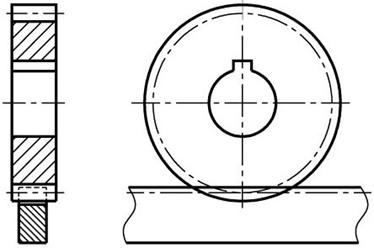
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращательного движения между валами со скрещивающимися осями.

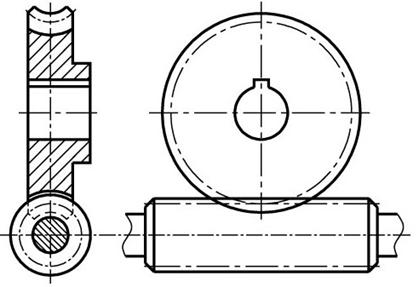
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).

Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …

Ряд 2: … 1,5; 3; 3,5; 6; 7 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращения при пересекающихся осях валов.

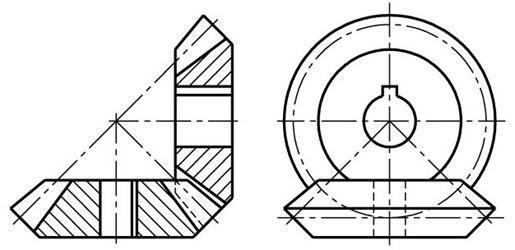
ГОСТ 9563-60 предусматривает два ряда модулей m  = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Видео:6.3 Зубчатые цилиндрические передачиСкачать

Расчет основных геометрических параметров цилиндрических прямозубых колес

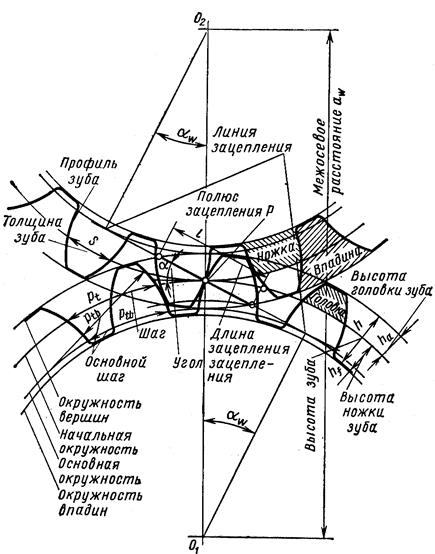
Эвольвентное зацепление двух зубчатых колес характеризуется следующим параметрами (ГОСТ 16530-70) (рис. 13.3).

Начальные окружности (d_w₁ и d_w₂) – воображаемые окружности, которые в процессе работы передачи перекатываются одна по другой без скольжения. Начальные окружности появляются у зубчатых колес в собранной передаче. Для отдельно взятого колеса понятие начальной окружности отсутствует. Оно имеет делительную окружность.

Окружность вершин зубьев (d_α) – окружность ограничивающая головки зубьев.

Окружность впадин (d_f) – окружность, проходящая через основания впадин зубьев.

Основная окружность (d_b₁ и d_b₂) – окружность, при развертке которой получается эвольвента.

Делительная окружность (d₁ и d₂) – окружность зубчатого колеса, по которой обкатывается делительная окружность (прямая) инструмента в процессе нарезания зубьев. Делительная окружность колеса является начальной только в процессе изготовления (нарезания) зубьев. У некорригированных колес и при высотной коррекции начальные и делительные окружности совпадают.

Полюс зацепления (точка “P”) – точка касания начальных окружностей.

Рис. 13.3. Элементы зубчатого зацепления

Окружной шаг зацепления (P_t) – расстояние между одноименными профилями, измеренное по дуге делительной окружности, зубчатого колеса.

Головка зуба (h_α) – часть зуба между делительной окружностью зубчатого колеса и его окружностью вершин зубьев.

Ножка зуба (h_f) – часть зуба между делительной окружностью и его окружностью впадин.

Высота зуба (h) равна сумме высот головки и ножки зуба.

Дуга зацепления (l) – путь по начальной окружности, проходимой точкой профиля за время зацепления пары сопряженных зубьев.

Коэффициент перекрытия (ε) – отношение дуги зацепления к окружному шагу.

Линия зацепления (N₁ и N₂) – линия, по которой перемещается точка касания зубьев. Линия зацепления проходит через полюс зацепления и является касательной к основным окружностям.

Угол зацепления (α_w) – угол между линией зацепления и касательной к начальным окружностям в полюсе зацепления.

Модуль зацепления (m). Все модули стандартизованы в пределах от 0,05 мм до 100 мм.

Рассмотренные параметры составляют определенные кинематические зависимости. В табл. 10 приводятся основные соотношения для цилиндрических некорригированных зубчатых передач внешнего зацепления.

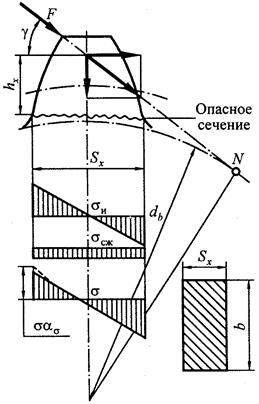
В расчётах зуб зубчатого колеса рассматривают как балку, защемленную одним концом и нагруженную силой (Q_n). Такое положение нагрузки принимается как наиболее опасное.

Наиболее опасное сечение, где наиболее вероятен излом зуба, находится у его корня в зоне наибольшей концентрации напряжений. Максимальное напряжение возникает на стороне сжатия (нерабочая сторона). Однако следует отметить то, что расчет на прочность необходимо производить по напряжению на рабочей стороне, т.к. на этой растянутой стороне зуба здесь может образоваться усталостная трещина.

Основные соотношения для цилиндрических
некорригированных зубчатых передач внешнего зацепления

Параметры зацепления	Формулы
Окружной модуль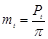
Нормальный модуль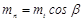
Нормальный шаг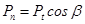
Межосевое расстояние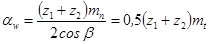
Высота головки зуба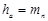
Высота ножки зуба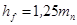
Высота зуба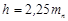
Радиальный зазор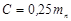
Делительный диаметр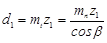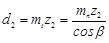
Начальный диаметр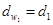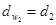
Диаметр основной окружности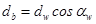
Диаметр вершин зубьев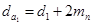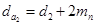
Диаметр впадин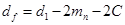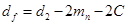
Коэффициент перекрытия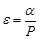

13.3. Расчет зубьев
цилиндрических прямозубых зубчатых колес на изгиб

— для обозначения расчета на изгиб, который проводится по ножке зуба принят индекс F (от термина ножка – Fut – на английском и немецком языках).

— для обозначений расчета на контактную прочность принят индекс H, в честь автора теории расчетов контактных напряжений Г. Герца.

Расчет ведется по расчетной окружной силе (q), отнесенной к единице ширины венца.

где: P – передаваемое окружное усилие;

b – ширина венца зубчатого колеса (длина зуба);

K – коэффициент нагрузки, учитывающий дополнительные вредные явления (удары).

q – расчетная окружная сила, отнесенная к единице ширины венца (b).

Нормальная удельная сила равна:

Перенесем силу давления q_n вдоль линии ее действия (линия зацепления) в точку, расположенную на оси симметрии зуба (рис. 13.4) и разложим на две составляющие: изгибающую зуб (q_ncosα_n), вызывающую в опасном сечении напряжения изгиба (σ_u) и сжимающую зуб (q_nsinα), вызывающую в зубе напряжения сжатия (σ_c_ж). Угол «γ» несколько больше угла профиля «α_w» (γ = α_w = 20˚).

Номинальное напряжение в опасном сечении:

;
;

;
;
.

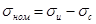
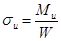
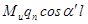
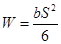
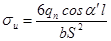
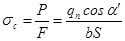
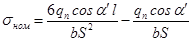
Рис. 13.4. Схема расчета зубьев на изгиб

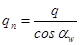
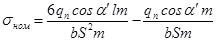
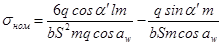
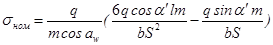
Умножим числитель и знаменатель на модуль «m» и заменим получим:

;

приняв: ;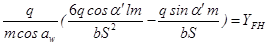

получим: .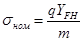

;

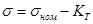
обозначив:

получим: ,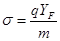

где: K_T – теоретический коэффициент концентрации напряжений;

Y_FHU, Y_F – коэффициенты прочности зубьев соответственно по номинальным и местным напряжениям;

Y_FH – представляет собой номинальное напряжение в опасном сечении зуба при m = 1 и q = 1, а Y_F – местное напряжение при тех же условиях.

Технические расчеты удобно вести по формулам, в которых условия нагружения заданы в форме номинальных крутящих моментов М (ктс.см) или мощности (кВт), частоты вращения n (об/мин) и коэффициента нагрузки К.

;

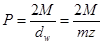
Для технических проверочных расчетов следует умножить P.K и приняв

получим: ;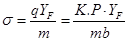

если

то: .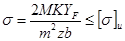

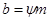
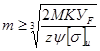
Модуль и ширина зубчатого венца, прежде всего, определяют прочность зуба на изгиб. Приняв и решив последнее уравнение относительно модуля, после преобразований получим:

Наиболее рациональной формой расчет, обеспечивающей равнопрочностъ зубьев по выкрашиванию и излому, является определение модуля по известному межосевому расстоянию “a_w” и ширине зубчатого венца “b” полученным из расчета на конкретную прочность.

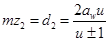
После преобразования получим:

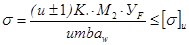
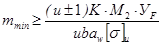
Для большинства редукторов общего назначения:

;

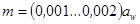
коэффициент нагрузки К можно выразить:

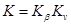
здесь: K_β – коэффициент концентрации нагрузки;

K_v – коэффициент динамичности нагрузки.

Видео:Что такое МОДУЛЬ шестерни? Ты ТОЧНО поймешь!Скачать

Выполнение эскиза зубчатого колеса

Последовательность выполнения эскизов деталей изложена в п. 6.12. Здесь дополнительно рассмотрим лишь то, что относится к зубчатым колесам.

Общий порядок выполнения эскиза зубчатого колеса следующий: определяют модуль и число зубьев; подсчитывают основные параметры зубчатого колеса; выполняют эскиз.

Видео:4 5 расчет зубчатого колесаСкачать

Определение модуля и числа зубьев

При подсчете числа зубьев обычно помечают мелом один из зубьев и от него по окружности подсчитывают их число. Пусть оно равно 68.

Для определения модуля надо воспользоваться приведенной ранее для подсчета диаметра окружности вершин формулой da = m(z + 2), откуда т = da/(z + 2); число зубьев нам известно.

Диаметр окружности вершин измеряют штангенциркулем, как показано на рис. 8.9. Пусть он равен 203 мм.

Рис. 8.9. Измерение диаметра окружности вершин зубьев зубчатого колеса

Подставив в формулу т = da/(z + 2) полученные данные, имеем т = 203/(68 + 2) = 203/70 = 2,9.

Значение модуля сопоставляют со стандартными, приведенными в п. 8.3 в соответствии с ГОСТ 9563–60, и выбирают ближайший, т.е. 3 мм.

Ошибка на 0,1 мм может получиться в результате неточного обмера и износа колеса.

Итак, в нашем примере число зубьев z = 68, а модуль т = 3.

Видео:SolidWorks. Цилиндрические зубчатые колесаСкачать

Подсчет основных параметров зубчатого колеса

Чтобы условно изобразить зубчатый венец, определяют диаметр трех окружностей.

Если при подсчете модуля результат несколько отличался от стандартного вследствие износа поверхности вершин, то тогда необходимо определить диаметр окружности вершин, т.е. наружный диаметр колеса. Подставив в формулу da = m(z + 2) число зубьев и модуль, получим da = 3(68+ 2) = 210 мм.

Диаметр делительной окружности подсчитывают по формуле d. = mz = 3 • 68 = 204 мм.

Диаметр окружности впадин подсчитывают по формуле df = d- 2,5т = 204 – 2,5•3 = 196,5 мм.

Из этих трех размеров на эскизе проставляют, как было указано, лишь диаметр окружности вершин.

Остальные размеры берут с натуры. Когда выполняют чертеж колеса, не имея натуры, эти размеры подсчитывают по соотношениям, приведенным в табл. 8.1. При этом диаметр вала выбирают в соответствии с ГОСТ 6636–69, а размеры шпоночного паза – в зависимости от диаметра вала по ГОСТ 23360-78.

На рабочих чертежах поля допусков и предельных отклонений шпоночных пазов записывают по следующему образцу, например: 10N9(-0,036) или 10Р9(-0,036) – паз вала; 10Is9(±0,018) – паз втулки.

Видео:Зубчатые передачиСкачать

Выполнение эскиза

Эскиз выполняют в соответствии с определенными размерами. Зарисовывают вид слева, проводя три концентрические окружности (рис. 8.10, а), диаметры которых в нашем примере da = 210 мм, d = 204 мм, df = = 196,4 мм. Зарисовывают фронтальный разрез, определяя границы зубьев с помощью линий связи (рис. 8.10, а).

Рис. 8.10. Последовательность выполнения эскиза цилиндрического зубчатого колеса

Зарисовывают на виде слева и разрезе отверстие для вала, шпоночный паз и другие конструктивные элементы. Затем обводят окружности вершин сплошной основной линией, делительную – штрихпунктирной, а впадин – сплошной тонкой линией (рис. 8.10, б). Заштриховывают разрез колеса, оставляя незаштрихованными зубья, на изображении которых проводят штрихпунктирные линии, соответствующие делительной окружности. Наносят размерные линии и размерные числа, обозначение шероховатости поверхностей, предельные отклонения формы и расположения поверхностей, заполняют таблицу параметров, записывают технические требования, заполняют основную надпись. Чертеж зубчатого колеса выполняют аналогично.

Когда выполняют чертеж цилиндрического зубчатого сектора, т.е. колеса, имеющего неполный зубчатый венец, то в таблице параметров помещают данные, характеризующие полное цилиндрическое колесо. Число зубьев указывают тоже для полной окружности. Это делается для выбора зуборезного инструмента, который маркируется модулем и числом зубьев. Фактическое число зубьев в секторе указывают в таблице параметров в третьей, справочной ее части.

Видео:Моделирование цилиндрического зубчатого колеса с прямыми зубьямиСкачать

Особенности чертежей цилиндрических колес с косыми зубьями

Для достижения более плавной передачи вращательного движения применяют зубчатые колеса не с прямыми, а с косыми или шевронными зубьями. Колесо с косыми зубьями нарисовано на рис. 8.5, б. Шевронные колеса можно представить себе как составленные из двух колес с разным направлением зубьев – одно с правым, другое с левым направлением (см. рис. 8.5, в).

Для колес с косыми зубьями различают нормальный модуль (тn) и торцовый (ms). Нормальный модуль определяют по так называемому нормальному сечению зуба, которое получается сечением плоскости, перпендикулярной длине зуба. Торцовый модуль определяют по плоскости торца колеса, т.е. как и у колес с прямым направлением зубьев.

Если угол наклона зуба к оси колеса равен β, то нормальный модуль определяют через торцовый по формуле тn = = mscos β.

Диаметр делительной окружности колеса с косыми зубьями определяют по формуле d = zms или по формуле d = = (zmn)cos β, если дан нормальный модуль.

Высота головки зуба (ha) у косозубых колес равна нормальному модулю (ha = тn), а высота ножки зуба равна 1,2тп нормального модуля (hf = l,2mn).

Диаметр окружности вершин у цилиндрических косозубых колес подсчитывают по формуле da = d+ 2тn, а диаметр окружности впадин – по формуле df=d- 2,4тn.

Зубчатое колесо с косыми зубьями изображено на рис. 8.7. Этот чертеж отличает то, что в таблице параметров приведен модуль нормальной тп, угол наклона зуба β, направление зуба, толщина зуба по хорде в нормальном сечении Sxn, ход винтовой линии Рt.