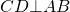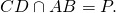- Ваш ответ
- решение вопроса
- Похожие вопросы
- Хорда перепендикулярна диаметру
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,013
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Хорда перепендикулярна диаметру
Если хорда перпендикулярна диаметру, то диаметр проходит через её середину.
Дано : окружность (O;R), AB — диаметр,
Соединим концы хорды CD с точкой O — центром окружности.
Рассмотрим прямоугольные треугольники COP и DOP.
1) OP — общий катет.
2) CO=DO (как радиусы).
Следовательно, треугольники COP и DOP равны (по катету и гипотенузе).
Что и требовалось доказать .
Так как CO=DO (как радиусы), то треугольник COD — равнобедренный с основанием CD, а OP — его высота, проведённая к основанию.
По свойству равнобедренного треугольника, OP является также его медианой.
Таким образом, если диаметр окружности перпендикулярен хорде, то он проходит через её середину.
Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью |
| Свойства хорд и дуг окружности |
| Теоремы о длинах хорд, касательных и секущих |
| Доказательства теорем о длинах хорд, касательных и секущих |
| Теорема о бабочке |
Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||
| Круг |  | |||||||||||||||||||||||||||
| Радиус |  | |||||||||||||||||||||||||||
| Хорда |  | |||||||||||||||||||||||||||
| Диаметр |  | |||||||||||||||||||||||||||
| Касательная |  | |||||||||||||||||||||||||||
| Секущая |  | |||||||||||||||||||||||||||
| Окружность |
|
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Конечная часть плоскости, ограниченная окружностью
Отрезок, соединяющий центр окружности с любой точкой окружности
Отрезок, соединяющий две любые точки окружности
Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности
Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания
Прямая, пересекающая окружность в двух точках
Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
|
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Большая из двух хорд расположена ближе к центру окружности.
У равных дуг равны и хорды.
Дуги, заключённые между параллельными хордами, равны.
Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | ||||||||||||||||
| Пересекающиеся хорды |  | |||||||||||||||||
| Касательные, проведённые к окружности из одной точки |  | |||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки |  | |||||||||||||||||
| Секущие, проведённые из одной точки вне круга |  | |||||||||||||||||
| Пересекающиеся хорды | ||
| ||
| Касательные, проведённые к окружности из одной точки | ||
| ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
| ||
| Секущие, проведённые из одной точки вне круга | ||
| ||
| Пересекающиеся хорды |
|
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.