Диаметр окружности описанной около прямоугольного треугольника совпадает с одной

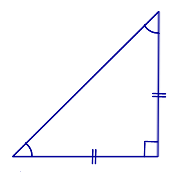Определение равнобедренного прямоугольного треугольника:

Равнобедренным прямоугольным треугольником называют такой прямоугольный треугольник, у которого равны катеты.

Свойство углов прямоугольного треугольника:

Острые углы равнобедренного прямоугольного треугольника равны 45° .

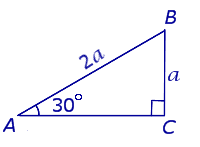Свойство прямоугольного треугольника с углом в 30° :

Катет прямоугольного треугольника, лежащий против угла в 30° , равен половине гипотенузы.

Признак прямоугольного треугольника с углом в 30° :

Если в прямоугольном треугольнике один из катетов равен половине гипотенузы, то этот катет лежит против угла в 30° .

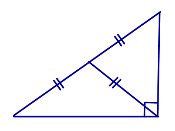Свойство медианы, проведенной к гипотенузе прямоугольного треугольника:

Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы.

Признак прямоугольного треугольника:

Если в треугольнике медиана равна половине стороны, к которой она проведена, то такой треугольник является прямоугольным.

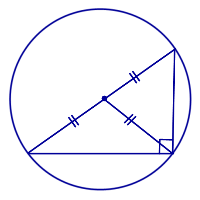Свойство окружности, описанной около прямоугольного треугольника:

Середина гипотенузы прямоугольного треугольника является центром описанной около него окружности.

Признак прямоугольного треугольника:

Если в треугольнике центр описанной окружности лежит на одной из сторон, то этот треугольник является прямоугольным треугольником, а центр описанной окружности совпадает с серединой гипотенузы.

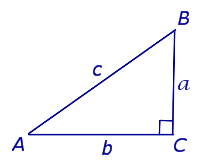В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Обратная теорема Пифагора:

Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник является прямоугольным

Видео:Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу.Скачать

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

Видео:ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ| Радиус окружности, описанной около прямоугольного треугольника, равен 4. НайСкачать

Диаметр окружности описанной около прямоугольного треугольника совпадает с одной

Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность

Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.

Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.

Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.

Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности

• Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.
• В любой треугольник можно вписать окружность, и только одну.
• Радиус вписанной в треугольник окружности равен отношению площади треугольника и его полупериметра: $$r = frac

  $$ , где S — площадь треугольника, а $$p =frac$$ — полупериметр треугольника.

Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.

Окружность называется описанной около треугольника, если она проходит через три его вершины.

• Вокруг любого треугольника можно описать окружность, и только одну.
• В любом треугольнике сторона равна произведению диаметра описанной окружности и синуса противолежащего угла.
• Площадь треугольника равна отношению произведения длин всех его сторон к учетверенному радиусу окружности, описанной около этого треугольника: $$R =frac$$, где S — площадь треугольника.

• Центр вневписанной окружности лежит на пересечении биссектрис внешних углов, при вершинах касаемой стороны, и биссектрисы угла при третей вершине.

Окружность, вписанная в прямоугольный треугольник

• Радиус вписанной окружности находят по формулам: $$r = frac$$, и $$r = frac$$, где a и b катеты прямоугольного треугольника, а c гипотенуза прямоугольного треугольника.

Окружность, описанная около прямоугольного треугольника

• Центр описанной окружности совпадает с серединой гипотенузы.
• Радиус равен половине гипотенузы: $$R = frac$$.
• Радиус равен медиане, проведенной к гипотенузе: $$R = m_$$.

Четырехугольник, вписанный в окружность

• Четырехугольник можно вписать в окружность, если сумма противолежащих углов равна $$180^circ: alpha + beta + gamma +delta = 180^circ$$.
• Если четырехугольник вписан в окружность, то суммы противолежащих углов равны $$180^circ$$.
• Сумма произведений противолежащих сторон четырехугольника ABCD равна произведению диагоналей: $$ABcdot DC + AD cdot BC = BD cdot AC$$.
• Площадь: $$S = sqrt$$, где $$p = frac$$ — полупериметр четырехугольника.

Окружность, вписанная в ромб

• В любой ромб можно вписать окружность.
• Радиус r вписанной окружности: $$r = frac$$, где h — высота ромба или $$r = frac <d_cdot d_>$$, где a — сторона ромба, d₁ и d₂ — диагонали ромба.

📹 Видео

Геометрия Найдите диаметр окружности, описанной около прямоугольного треугольника, если один из егоСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Как найти диаметр окружности, описанной около равнобедренного треугольникаСкачать

Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

ТЕОРИЯ: ОКРУЖНОСТЬ ОПИСАННАЯ ОКОЛО ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА (Кратко)Скачать

Нахождение диаметра описанной окружностиСкачать

Построить описанную окружность (Задача 1)Скачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

Окружность, описанная около прямоугольного треугольника | Геометрия 8-9 классыСкачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

Математика ОГЭ Задание 26 Прямоугольный треугольник Описанная и вписанная окружностиСкачать

Радиус окружности, описанной около прямоугольного треугольника. ЗадачаСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

№704. Окружность с центром О описана около прямоугольного треугольника, а) ДокажитеСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать