Диаметр окружности описанной около прямоугольного треугольника равен

Геометрия | 5 — 9 классы

Диаметр окружности описанной около прямоугольного треугольника равен 18 см найдите длину медианы проведенной из вершины прямого угла этого треугольника.

Все вершины прямоугольного треугольника лежат на описанной окружностигипотенуза равна диаметрумедиана, проведенная из вершины прямого угла попадает прямо в ЦЕНТР окружностиэто РАДИУС окружностиm = R = d / 2 = 18 см / 2 = 9 смответ 9 см.

Диаметр окружности, описанной около прямоугольного треугольника, равен 18 см?

Диаметр окружности, описанной около прямоугольного треугольника, равен 18 см.

Найдите гипотенузу треугольника.

Где расположен центр окружности?

В равнобедренном прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна 7 : √2 см?

В равнобедренном прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна 7 : √2 см.

Найдите площадь треугольника.

Медианы треугольника АВС, проведенные из вершин В и С, пересекаются под прямым углом?

Медианы треугольника АВС, проведенные из вершин В и С, пересекаются под прямым углом.

Найдите длину стороны ВС, если длина медианы треугольника, проведенной из вершины А, равна 18 см.

Один из острых Бугров прямоугольного треугольника равен 48° найдите градусную меру угла между высотой и медианы проведенным из вершины прямого угла?

Один из острых Бугров прямоугольного треугольника равен 48° найдите градусную меру угла между высотой и медианы проведенным из вершины прямого угла.

Найдите углы прямоугольного треугольника, если угол между биссектрисой и высотой проведенными из вершины прямого угла равен 15 градусам?

Найдите углы прямоугольного треугольника, если угол между биссектрисой и высотой проведенными из вершины прямого угла равен 15 градусам.

Угол между биссектрисой и высотой, проведенными из вершины прямого угла прямоугольного треугольника равен 12 градусов?

Угол между биссектрисой и высотой, проведенными из вершины прямого угла прямоугольного треугольника равен 12 градусов.

Найдите острые углы треугольника.

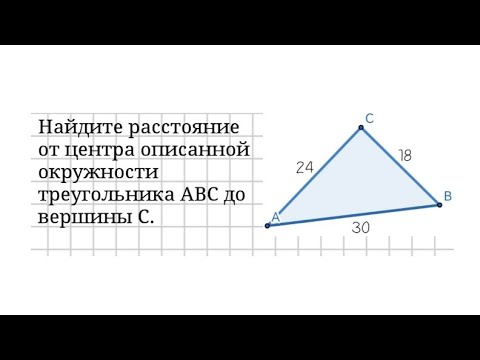
Найдите длину боковой стороны равнобедренного прямоугольного треугольника, если известно, что диаметр описанной около него окружности равен 56?

Найдите длину боковой стороны равнобедренного прямоугольного треугольника, если известно, что диаметр описанной около него окружности равен 56.

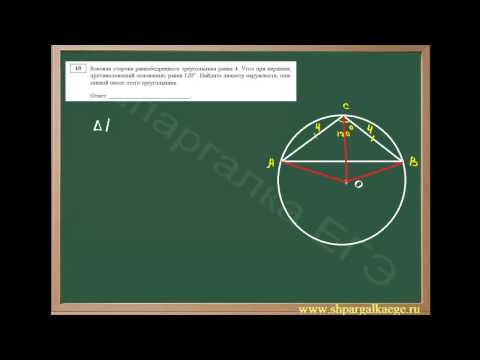
Угол между высотой и биссектрисой, проведенными из вершины прямого угла прямоугольного треугольника, равен 8 градусам?

Угол между высотой и биссектрисой, проведенными из вершины прямого угла прямоугольного треугольника, равен 8 градусам.

Найдите острые углы треугольника.

Один из острых углов прямоугольного треугольника равен 40?

Один из острых углов прямоугольного треугольника равен 40.

Определите острый угол между радиусом описанной окружности, проведенным в вершину прямого угла, и гипотенузой.

Угол между высотой прямоугольного треугольника проведенной из вершины прямого угла, и биссектрисой прямого угла равен 12 градусов найти острые углы прямоугольного треугольника?

Угол между высотой прямоугольного треугольника проведенной из вершины прямого угла, и биссектрисой прямого угла равен 12 градусов найти острые углы прямоугольного треугольника.

Вы открыли страницу вопроса Диаметр окружности описанной около прямоугольного треугольника равен 18 см найдите длину медианы проведенной из вершины прямого угла этого треугольника?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Вот посмотри если в первом что то не понятно мне все равно я свое дело сделал.

Значит так, у нас есть смежные и верти кальные углы смежные в сумме дают 180 градусов, а вертикальные равны если ты нарисуешь крестик , то верхние углы смежные значит 180 — 94 ты получаешь 2 угол вертикальные углы это 1. 2 + 3. 4. Углы 3 и 2 , и4 и..

Сумма двух углов по одной стороне параллелограмма = 180° 1) если один угол = х°, то другой = 2х (по условию) х + 2х = 180 3х = 180 х = 60 2х = 120 Противолежащие углы параллелограмма равны, ⇒ углы параллелограмма = 60° ; 120° ; 60° ; 120° — — — — — -..

Пусть это пирамида будет PABCD, тогда диагональ прямоугольнтка будет равна АСквадрат = АDквадр + DCквадр ; АС = 12 ; пусть высота будет РО , и тогда она равна половине диагонали — 12 : 2 = 6 ; РОквадр = АРквад — АОквадр ; высота = 8.

6×6 = 36 значит ответ 6см его сторона.

Дано : шар ; AC = R = 13 см ; AB = 5 см. S (ω, B, BC) — ? Решение : · рассмотрим треугольник ABC — прямоугольный ; · по теореме Пифагора : BC² = AC² — AB², BC (см). BC = r (ω, B, BC) = 12 см ; · площадь сечения (окружности) : S = πr² = BC²π, S = 1..

Углы равны. Бесиктрисса делит угол на две равные части. Угол BCA = углу BAC.

Через прямую (а) и не лежащуюна ней точку (В) можно провести плоскость, притом только одну. Точки А и В лежат и в плоскостиα, и в плскостиβ. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. Все точки прямой АВ п..

X + 50 + x + 50 + x + x = 360 4x + 100 = 360 4x = 260 x = 65 — углы AOD и BOC 65 + 50 = 115 — углы AOB и DOC.

Так как угол CDK = 45 и угол СКД равен 90, то по теореме о сумме углов угол КСД равен 45, поэтому треугольник СКД равнобедренный и стороны СК и КД равны QA = CK = КД = 6 как отрезки, заключенные между параллельными прямыми QAKC — прямоугольник, поэто..

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов

Серединный перпендикуляр к отрезку

Окружность описанная около треугольника

Свойства описанной около треугольника окружности. Теорема синусов

Доказательства теорем о свойствах описанной около треугольника окружности

Серединный перпендикуляр к отрезку

Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.

Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.

Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .

Докажем, что отрезок AE длиннее отрезка EB . Действительно,

Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,

Полученное противоречие и завершает доказательство теоремы 2

Окружность, описанная около треугольника

Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .

Свойства описанной около треугольника окружности. Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Фигура	Рисунок	Свойство
Серединные перпендикуляры к сторонам треугольника		Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство
Окружность, описанная около треугольника		Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство
Центр описанной около остроугольного треугольника окружности		Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центр описанной около прямоугольного треугольника окружности		Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство
Центр описанной около тупоугольного треугольника окружности		Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Теорема синусов
Площадь треугольника
Радиус описанной окружности

Серединные перпендикуляры к сторонам треугольника

Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Окружность, описанная около треугольника

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центр описанной около прямоугольного треугольника окружности

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Теорема синусов

Для любого треугольника справедливы равенства (теорема синусов):

,

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Площадь треугольника

Для любого треугольника справедливо равенство:

где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Радиус описанной окружности

Для любого треугольника справедливо равенство:

где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.

Доказательства теорем о свойствах описанной около треугольника окружности

Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).

Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:

Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:

Следовательно, справедливо равенство:

откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.

Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).

При доказательстве теоремы 3 было получено равенство:

из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.

Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

.

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:

l = 2Rsin φ .

(1)

Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.

Формула (1) доказана.

Из формулы (1) для вписанного треугольника ABC получаем (рис.7):

Радиус описанной окружности около прямоугольного треугольника онлайн

С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус описанной окружности около прямоугольного треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Открыть онлайн калькулятор

1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника

Пусть известна гипотенуза c прямоугольного треугольника (Рис.1). Найдем радиус описанной окружности около треугольника.

На странице Радиус окружности описанной около треугольника формула радиуса описанной окружности около треугольника по стороне и противолежащему углу имеет вид:

( small R=frac )

где C − угол противолежащий гипотенузе прямоугольного треугольника. Поскольку угол, противолежащий гипотенузе − прямой, то получим:

( small R=frac=frac, )

( small R=frac. )

(1)

Пример 1. Известна гипотенуза ( small с=frac ) прямоугольного треугольника. Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (1).

Подставим значение ( small c=frac ) в (1):

Ответ:

2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника

Пусть известны катеты a и b прямоугольного треугольника. Найдем радиус описанной окружности около треугольника (Рис.2).

Из теоремы Пифагора запишем формулу гипотенузы, выраженная через катеты:

( small c=sqrt. )

(2)

Подставляя (2) в (1), получим:

( small R=frac=frac<large sqrt>, )

( small R=frac<large sqrt>. )

(3)

Пример 2. Катеты прямоугольного треугольника равны: ( small a=15 , ; b=3.) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (3). Подставим значения ( small a=15 , ; b=3) в (3):

Ответ:

3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника

Формула для вычисления радиуса окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника аналогична формуле вычисления радиуса описанной окружности около произвольного треугольника (см. статью на странице Радиус описанной окружности около треугольника онлайн):

(4)

4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника

Пусть известны катет a и прилежащий острый угол B прямоугольного треугольника (Рис.4). Найдем радиус описанной окружности около треугольника.

Так как треугольник прямоугольный, то сумма острых углов треугольника равна 90°:

( small angle A+angle B=90°. )

( small angle A=90°-angle B. )

(5)

Подставляя (5) в (4), получим:

( small R=frac=frac) ( small =frac )

( small R=frac. )

(6)

Пример 3. Катет прямоугольного треугольника равен: ( small a=15 ,) а прилежащий угол равен ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.

Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (6). Подставим значения ( small a=15 , ; angle B=25° ) в (6):

Ответ: