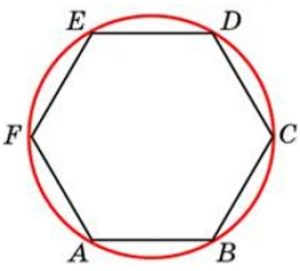
Диаметр окружности через периметр шестиугольника (4 видео)

Диаметр окружности через периметр шестиугольника

Задание 6. Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.

Если периметр равен 72, то одна сторона шестиугольника равна

Известно, что центр описанной окружности O вокруг правильного шестиугольника с одной из его сторон, например, ED образуют равносторонний треугольник, то есть треугольник EOD – равносторонний. Радиус описанной окружности равен стороне шестиугольника ED=12, а диаметр 24.

Содержание

Решение №2077 Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.
Формулы для расчета периметра шестиугольника
Описание фигуры
До начала вычислений
Первый вариант
Правильный шестиугольник
Иные варианты расчета
Видео
Видео

Видео:Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.Скачать

Решение №2077 Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.

Найдем сторону шестиугольника:

108:6 = 18

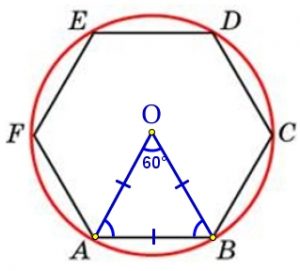
Рассмотрим треугольник AOB. Он равносторонний, т.к. ∠АОВ = 360°/6 = 60°, АО = ОВ. Тогда радиус равен стороне шестиугольника:

АВ = ОВ = r = 18

Найдём диаметр:

d = 2·r = 2·18 = 36

Ответ: 36.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.

Видео:Радиус и диаметрСкачать

Формулы для расчета периметра шестиугольника

Иногда возникает необычная для учащегося задача по нахождению периметра шестиугольника. Не всегда на этот вопрос можно ответить сразу. В этой статье мы рассмотрим подробным образом, как найти периметр шестиугольника согласно формулам, а также вычислить и находить его другими способами.

Видео:Периметр правильного шестиугольника равен 150. Найдите диаметр описанной около него окружности (ЕГЭ)Скачать

Описание фигуры

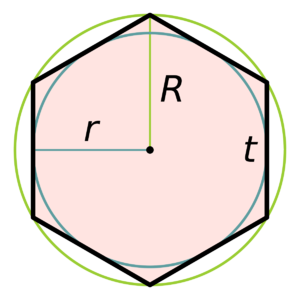
Непосредственно шестиугольник представляет собой плоскую фигуру, состоящую из шести отрезков, с расположением под углом 120 градусов относительно друг друга. Имеет научное название гексагон. Вокруг него или внутри можно вписать либо описать окружность. Между собой радиус и сторона многоугольника соотносятся по следующим формулам:

Гексагон является очень популярной фигурой, ее имеют гайки, карандаши, соты, снежинки и многое другое. Является оптимальным вариантом для того, чтобы без пробелов замостить все пространство. Одним из примеров этого является Мостовая гигантов, образовавшаяся в результате соединения более чем 40 тысяч базальтовых колонн в результате извержения древнего вулкана и элегантно замостившая поверхность побережья в Северной Ирландии.

Поиски вышеописанного параметра гексагона являются простой, но в то же время довольно интересной задачей. Найдя периметр, можно убедиться в правильности замощенного пространства и отсутствии пробелов при составлении будущей документации.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

До начала вычислений

Всем известно, что периметр плоской фигуры, к которой относится шестиугольник, является ничем иным, как длиной ограничивающей линии. Для нахождения периметра такой фигуры как гексагон, достаточно будет найти и сложить длины всех его сторон. Чтобы произвести эту процедуру, нужно измерить длины всех составляющих его отрезков. Значительно облегчается задача, если данная фигура имеет правильную форму. Разберем далее, как нужно искать периметр шестиугольника.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Первый вариант

Инструментарий достаточно простой. Понадобятся всего лишь циркуль и линейка. Вычислять периметр гексагона нужно следующим образом: измерить линейкой длину каждой из 6 сторон и сложить полученные значения. Все измерения длин сторон должны иметь единую систему единиц, тогда достаточно будет сложить числовые значения. То есть, единица измерения параметра шестиугольника совпадет с аналогичными параметрами длин отрезков.

Например, имеются следующие отрезки: 2 сантиметра, 5,4,3,2 и 1 миллиметр. В этом случае нужно перевести 2 сантиметра в миллиметры из расчета 1 сантиметр равняется 10 миллиметрам и суммируете P=20+5+4+3+2+1=35 миллиметров. Таким образом рассчитывается периметр большинства видов шестиугольников.

Видео:Геометрия - Построение шестиугольникаСкачать

Правильный шестиугольник

В случае, если шестиугольник имеет правильную форму, то расчет нужного параметра становится гораздо проще.

Умножьте длину его стороны на 6 и вы получите нужное значение по формуле P=a*6, где a — сторона правильного шестиугольника.
Например, у нас имеется фигура со стороной длиной 10 сантиметров, умножаем 10 на 6 и получаем в итоге 60 сантиметров в периметре.
Также правильная фигура имеет уникальное свойство: радиус окружности, который описан вокруг такого шестиугольника, равен длине его стороны. Если вам известен радиус описанной окружности, то достаточно воспользоваться формулой в виде P=R*6, где R — радиус описанной окружности.

Например, известен прямоугольник, вписанный в окружность, имеющую диаметр 20 сантиметров. Тогда радиус будет в два раза меньше и составит 10 сантиметров. Полученную величину умножаем на 6 сторон и получаем периметр.

Видео:Длина окружности. Математика 6 класс.Скачать

Иные варианты расчета

Если известен радиус вписанной в многоугольник окружности, рекомендуется использовать формулу P=4sqrt (3)*r, в которой r является радиусом вписанной окружности.

Можно высчитать периметр многоугольника, если в условии известна площадь. Площадь находится по формуле: S=3/2*sqrt (3)*a 2 , где S является площадью правильного шестиугольника. Далее находим из формулы a=sqrt (2/3*S/sqrt (3)). Найдя a, можно отыскать периметр, а именно P=6*a=6*sqrt (2/3*S/sqrt (3))=2*sqrt (2*s*sqrt (3)).

Другие способы измерения периметра шестиугольника можно найти в специализированной литературе и на особых порталах.

Шестиугольник относят к очень эффективной фигуре. Она встречается как в реальности, так и среди природных явлений. Если же вы боитесь, что не сможете правильно сами посчитать заданную величину, на помощь придут специальные онлайн-калькуляторы, в которых можно ввести необходимые данные для вычисления периметра. Удачной математической работы с поисками периметра для гексагона.

Видео:Периметр правильного шестиугольника равен 222. Найдите диаметр описанной окружности.Скачать