Диаметр окружности через хорду и расстояние от центра

Бывают ситуации, когда необходимо измерить диаметр чего-либо, например, трубопровода, но нет возможности измерить длину окружности (из-за изоляции или температуры).

В этом случае можно применить метод вычисления диаметра по хорде. Для этого метода необходим только штангенциркуль.

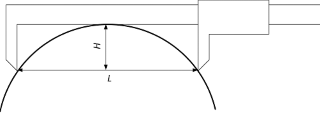
1. Прикладываем его, как показано на рис. 1;
2. измеряем длину L;
3. измеряем высоту губок штангенциркуля Н;
4. вычисляем диаметр по формуле D = (L 2 ⁄ 4H) + H или
5. вычисляем радиус по формуле r = (L 2 + 4H 2 ) ⁄ 8H

Рисунок 1

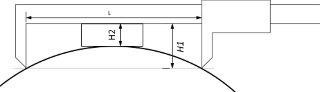
Если под рукой только «штангель» с длинными губками или не хватает его измеряемого диапазона можно применить какую-нибудь «проставку». В идеале подойдёт плоскопараллельная концевая мера… 😉 Её надо вставить, как показано на рисунке 2, и при вычислении, от длины губок отнять высоту этой «проставки». Н = Н1 — Н2

Рисунок 2

Точность этого метода зависит, только от инструмента, который Вы будете применять.

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

Как найти диаметр окружности

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.

Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.

Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.

Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.

Радиус — отрезок, который соединяет центр окружности и любую точку на ней.

Как узнать диаметр. Формулы

В данной теме нам предстоит узнать три формулы:

1. Общая формула.

Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.

2. Если перед нами стоит задача найти диаметр по длине окружности

D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.

Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.

3. Если есть чертеж окружности

• Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.

• Отметить точки пересечения прямой и окружности.

• Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.

• Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.

• Теперь осталось измерить диаметр круга при помощи линейки. Получилось!

Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.

📹 Видео