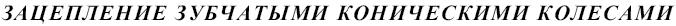Диаметр начальной окружности зубчатого колеса

Видео:Что такое МОДУЛЬ шестерни? Ты ТОЧНО поймешь!Скачать

Зацепления зубчатые относятся к передачам (подвиж­ным соединениям) и передают движение от двигателя к ис­полнитель­ным механизмам. К составным частям зубчатых передач отно­сятся зубчатые колеса (цилиндрические, кони­ческие), червяки, рейки.

Диаметр делительной ок­ружности d является од­ним из основных параметров, по кото­рому произ­водят расчет зубча­того ко­леса:

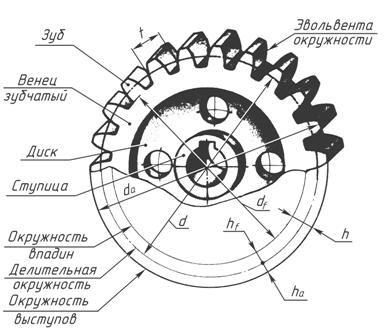
где z – число зубьев;

Модуль зацепления m – это часть диаметра делительной ок­ружности, приходящейся на один зуб:

где t – шаг зацепления.

где h _a – высота головки зуба, h _a = m ; h _f – высота ножки зуба, h _f = 1,25 m .

Диаметр окружности выступов зубьев :

Диаметр окружности впадин :

Служит для передачи вращения при параллельных осях валов.

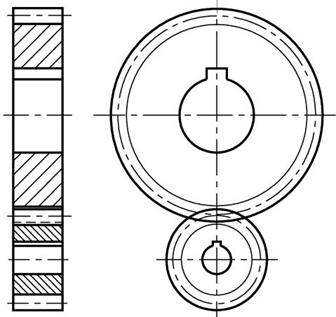
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2 .

Служит для преобразования вращательного движения в возвратно-посту­пательное.

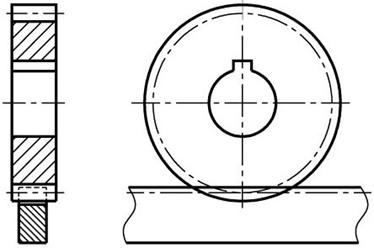
ГОСТ 9563-60 предусматривает два ряда модулей m = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращательного движения между валами со скрещивающимися осями.

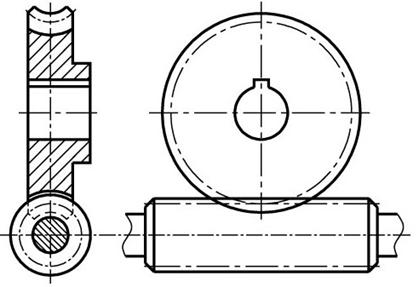
ГОСТ 19672-74 устанавливает два ряда значений модулей m (мм).

Ряд 1: … 1; 1,25; 1,6; 2; 2,5; 3,15; 4; 5; 6,3; 8; 10 …

Ряд 2: … 1,5; 3; 3,5; 6; 7 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Служит для передачи вращения при пересекающихся осях валов.

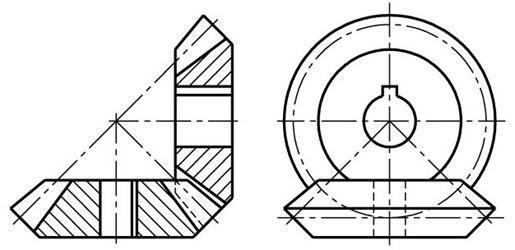
ГОСТ 9563-60 предусматривает два ряда модулей m  = 0,05…100 мм.

Ряд 1: … 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16 …

Ряд 2: … 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14 …

Примечание. Ряд 1 следует предпочитать ряду 2.

Видео:SolidWorks. Создание параметрического зубчатого колесаСкачать

Детали машин

Видео:Модуль шестерни и параметры зубчатого колесаСкачать

Геометрические параметры эвольвентного зацепления

Эвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие.

В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:

• w – начальной;
• b – основной;
• a – вершин зубьев;
• f – впадин зубьев.

Параметрам, относящимся к делительной окружности, индекс не присваивается.

При обозначении параметров пары зубчатых колес индекс «1» присваивается шестерне, «2» — колесу.

Начальные окружности

Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О₁ и О₂ до полюса П ) при неизменном межосевом расстоянии О₁О₂ тоже остается неизменным.
При изменении межосевого расстояния a_w меняются и диаметры d_w начальных окружностей шестерни и колеса, т. е. у пары зубчатых колес может быть множество начальных окружностей.
У отдельно взятого колеса начальной окружности не существует – по определению этот параметр образуется в зацеплении, т. е. в зубчатой передаче.

Межосевое расстояние определяется по формуле:

Делительная окружность

Окружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным.

Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.

У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.:

Исключение составляют передачи с угловой модификацией.

Окружной шаг зубьев

Расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1).
Для пары зацепляющихся зубчатых колес окружной шаг зубьев должен быть одинаковым.

Основной шаг

Этот параметр, обозначаемый p_b , относится к основной окружности. На основании второго и четвертого свойств эвольвенты расстояние по нормали между одноименными сторонами двух соседних зубьев равно шагу p_b .
Из треугольника О₂ВП (см. рис. 1) диаметр основной окружности d_b2 = 2 r_b2 = d₂ cos α_w , откуда основной шаг может быть определен по формуле:

Окружная толщина зуба и окружная ширина впадины

Окружная толщина зуба s_t и окружная ширина впадины e_t по дуге делительной окружности колеса передачи без смещения теоретически равны. Однако при изготовлении зубчатых колес на теоретический размер s_t назначают такое расположение поля допуска, при котором зуб получается тоньше, чем и гарантируется боковой зазор j (рис. 1), необходимый для нормального зацепления. По делительной окружности всегда s_t + e_t = p .

Окружной модуль зубьев

Из определения окружного шага следует, что длина делительной окружности зубчатого колеса πd = pz , где z – число зубьев. Следовательно,

Шаг зубьев p , так же как длина окружности, включает в себя трансцендентное число π , а поэтом шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число p/π , которое называют модулем зубьев , обозначают m и измеряют в миллиметрах:

d = mz или m = d/z .

Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.

Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм.
В соответствии со стандартным рядом I модуль может принимать следующие значения: 1,0, 1,25, 1,5, 2,0, 2,5, 3,0, 4,0, 5,0, 6,0, 8,0, 10,0.
Стандартный ряд II значительно расширяет диапазон применяемых на практике модулей ( m = 1,125, 1,375, 1,75 и т. д.).

При выборе модулей из стандартных рядов первый ряд следует предпочитать второму.

Высота головки и ножки зуба

Делительная окружность делит зуб по высоте на головку h_a и ножку h_f . Для создания радиального зазора с (см . рис. 1) необходимо

Для передачи без смещения h_a = m .

Длина активной линии зацепления

При вращении зубчатых колес точка зацепления S (см. рис. 1) пары зубьев перемещается по линии зацепления NN . Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S» пересечения линии зацепления с окружностью вершин шестерни.
Отрезок S’S» линии зацепления называют длиной активной линии зацепления и обозначают g_α . Длину g_α легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S» и замеряют g_α .

Коэффициент торцового перекрытия

Коэффициентом торцового перекрытия ε_α называют отношение длины активной линии зацепления к основному шагу:

где z₁ и z₂ – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса.

Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи.

За период работ пары зубьев точка их зацепления проходит путь, равный по длине g_α (см. рис. 1), а расстояние между профилями соседних зубьев по линии зацепления равно основному шагу p_b . При g_α > p_b необходимое перекрытие зубьев обеспечивается.

По условию непрерывности зацепления должно быть ε_α > 1. С увеличением количества зубьев z увеличивается и коэффициент торцового перекрытия ε_α .

Видео:Построение эвольвентного зацепленияСкачать

2.3. ЭВОЛЬВЕНТНЫЕ ЗУБЧАТЫЕ КОЛЕСА И ИХ ПАРАМЕТРЫ

Рисунок 3. Параметры эвольвентного зубчатого колеса.

К основным геометрическим параметрам эвольвентного зубчатого колеса относятся: модуль m, шаг p, угол профиля α, число зубьев z и коэффициент относительного смещения x.

Виды модулей: делительный, основной, начальный.

Для косозубых колес дополнительно различают: нормальный, торцевой и осевой.

Для ограничения числа модулей ГОСТом установлен стандартный ряд его значений, которые определяются по делительной окружности.

Модуль − это число миллиметров диаметра делительной окружности зубчатого колеса, приходящееся на один зуб.

Делительная окружность − это теоретическая окружность зубчатого колеса, на которой модуль и шаг принимают стандартные значения

Делительная окружность делит зуб на головку и ножку.

Начальная окружность – это теоретическая окружность зубчатого колеса, принадлежащая его начальной поверхности.

Головка зуба – это часть зуба, расположенная между делительной ок-ружностью зубчатого колеса и его окружностью вершин.

Ножка зуба – это часть зуба, расположенная между делительной окружностью зубчатого колеса и его окружностью впадин.

Сумма высот головки ha и ножки hf соответствует высоте зубьев h:

Окружность вершин – это теоретическая окружность зубчатого колеса, соединяющая вершины его зубьев.

Окружность впадин – это теоретическая окружность зубчатого колеса, соединяющая все его впадины.

Согласно ГОСТ 13755-81 α = 20°, С* = 0,25.

Коэффициент уравнительного смещения Δу:

Окружной шаг, или шаг p − это расстояние по дуге делительной окружности между одноименными точками профилей соседних зубьев.

Угловой шаг − это центральный угол, охватывающий дугу делительной окружности, соответствующий окружному шагу

Шаг по основной окружности − это расстояние по дуге основной ок-ружности между одноименными точками профилей соседних зубьев

Толщина зуба s по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей одного зуба

S = 0,5 · ρ + 2 · х · m · tg α

Ширина впадины e по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей со-седних зубьев

Толщина зуба Sb по основной окружности − это расстояние по дуге основной окружности между разноименными точками профилей одного зуба.

Толщина зуба Sa по окружности вершин − это расстояние по дуге ок-ружности вершин между разноименными точками профилей одного зуба.

Угол профиля α − это острый угол между касательной t – t к профилю зуба в точке, лежащей на делительной окружности зубчатого колеса и радиус-вектором, проведенным в данную точку из его геометрического центра

🌟 Видео

6.3 Зубчатые цилиндрические передачиСкачать

Как определить шестернюСкачать

#SolidWorks - Зубчатые колёсаСкачать

Зубчатые передачиСкачать

Расчёт ведущего колеса танка.Скачать

4 5 расчет зубчатого колесаСкачать

SolidWorks. Цилиндрические зубчатые колесаСкачать

Подборка САМЫХ "УМНЫХ" водителей #946Скачать

Механические передачи. Часть 1. История. Геометрия зубчатых колесСкачать

Форма зубьев колеса в зависимости от коэффициента смещенияСкачать

SolidWorks. Создание параметрического косозубого и шевронного зубчатого колесаСкачать

Геометрические параметры зубчатых колёс. Перекрытие. Смещение.Скачать

Зубчатые колесаСкачать

Зубчатое колесо в Компас 3DСкачать

Лекция «Цилиндрические зубчатые передачи. Основные параметры»Скачать

Построение параметрической модели зубчатого колесаСкачать