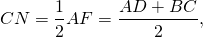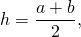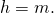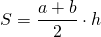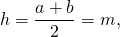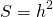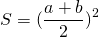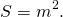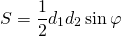Формат ответа: цифра или несколько цифр, слово или несколько слов. Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
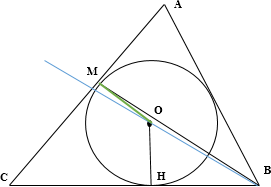
В треугольнике ABC угол ABC равен 60°. Окружность, вписанная в треугольник, касается стороны AC в точке M.
а) Докажите, что отрезок BM не больше утроенного радиуса вписанной в треугольник окружности.
б) Найдите sin∠BMC, если известно, что отрезок BM в 2,5 раза больше радиуса вписанной в треугольник окружности.
а) Проведем радиусы $OHperp BC$ и $OMperp AC$ с длинной $R.$ Так как центр вписанной окружности находится в точке пересечения биссектрис, то $angle OBH=30^.$ Катет, лежащий против угла в $30^$ равен половине гипотенузы $Rightarrow OB=2OH=2R.$ По неравенству треугольника для $OBM$ имеем $BM < OM+OB=3R.$
б) Запишем теорему косинусов для треугольника $OBM:$
$OB^=OM^-2OMcdot BMcos angle BMO,$
cos$angle BMO=displaystyle frac=0,65.$
Так как $angle OMC=90^,$ то $sin angle BMC=sin (90^+angle BMO)=cos angle BMO=0,65.$
Точка B лежит на отрезке AC. Прямая, проходящая через точку A, касается окружности с диаметром BC в точке M и второй раз пересекает окружность с диаметром AB в точке K. Продолжение отрезка MB пересекает окружность с диаметром AB в точке D.
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK=3 и MK=12.
а) Треугольники $ABD$ и $BMC$ — прямоугольные, так как опираются на диаметры окружностей. Тогда $AD$ и $CM$ перпендикулярны одной и той же прямой $DM$. Следовательно, $ADparallel MC.$
б) Пусть $O$ — центр окружности с диаметром $AB.$ Тогда отрезок $OM$ перпендикулярен $AM.$
Так как угол $AKB$ — вписанный, опирающийся на диаметр, то отрезок $KB$ перпендикулярен $AM.$ Значит, $ KBparallel OM $ и треугольники $AKB$ и $AOM$ подобны по двум углам:
$displaystyle frac=displaystyle frac=displaystyle frac=displaystyle frac,$
Проведем высоту $BP$ в треугольнике $BOP:$
Рассмотрим треугольники $ACM$ и $DCM.$ Они имеют одинаковые основания $MC$ и высоту $DM,$ а, значит, и равные площадию
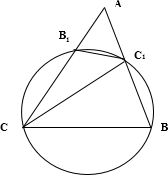
Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках C1 и В1 соответственно.
а) Докажите, что треугольник АВC подобен треугольнику АВ1С1.
б) Вычислите длину стороны ВС и радиус данной окружности, если ∠ А = 45∘, В1С1 = 6 и площадь треугольника АВ1С1 в восемь раз меньше площади четырёхугольника ВСВ1С1.
a) В треугольниках $ABC$ и $AB_C_$ $angle A$ — общий. $AC$ и $AB$ — секущие, проведениные из одной точки, следовательно, $displaystyle frac<AB_>=displaystyle frac<AC_>.$ Тогда треугольники $ABC$ и $ AB_C_$ подобны по двум сторонам и углу между ними.
б) Отношение площадей подобных фигур равно квадрату линейного отношения соответсвенных элементов данных фигур:
$displaystyle frac<S_<AB_C_>><S_>=left( displaystyle frac<B_C_>right)^=left( displaystyle frac<AC_>right) ^=left( displaystyle frac<AB_>right)^=displaystyle fracRightarrow BC=3B_C_=18.$
По теореме косинусов в треугольнике $ACC_:$
По теореме синусов $ACC_:$
Искомый радиус совпадает с радиусом окружности, описанной около треугольника $BCC_.$ по теореме синусов из треугольника $BCC_:$
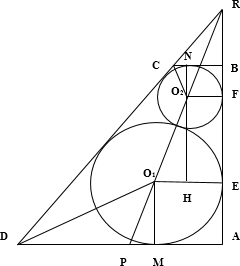
В прямоугольной трапеции ABCD с прямым углом при вершине A расположены две окружности. Одна из них касается боковых сторон и большего основания AD, вторая — боковых сторон, меньшего основания BC и первой окружности.
а) Прямая, проходящая через центры окружностей, пересекает основание AD в точке P. Докажите, что $displaystyle frac=sin angle D$.
б) Найдите площадь трапеции, если радиусы окружностей равны $displaystyle frac$ и $displaystyle frac$ .
а) Продолжим стороны $AB$ и $CD$ до пересечения в точки $R$. Окружности вписаны в угол, следовательно, их центры лежат на биссектрисе этого угла. Точка $P$ лежит на одной прямой с центрами окружности, значит, $RP$ — биссектриса треугольника $ARP.$
По теореме о биссектрисе угла треугольника $displaystyle frac=displaystyle frac=sin angle D.$
б) Введем обозначения. Пусть окружность с центром $O_$ и радиусом $displaystyle frac$ касается сторон $AB$ и $AD$ в точках $E$ и $M,$ а окружность в цетре $O_$ и радиусом $displaystyle frac$ касается сторон $AB$ и $BC$ в точках $F$ и $N.$ Проведем перпендикуляр $O_H$ к отрезку $O_E.$ Так как радиус, проведенный в точку касания, перпендикулярен касательной, то $HO_FE$ — прямоугольник, а $AEO_M$ и $BNO_F$ — квадраты. Получим:
$O_H=O_E-HE=O_E-O_F=displaystyle frac-displaystyle frac=1,$
$O_O_=displaystyle frac+displaystyle frac=displaystyle frac.$
По теореме Пифагора из трегугольника $O_O_H:$
Прямые $O_H$ и $EF$ параллельны, значит треугольники $O_O_H$ и $O_RE$ подобны по признаку подобия по двум углам ($angle REO_=angle O_HO_=90^,$ $angle RO_E$ — общий). Тогда обозначим $angle O_O_H=angle O_RE=alpha .$
Из прямоугольного треугольника $O_O_H:$
$tg alpha =displaystyle frac<O_H><O_H>=displaystyle frac.$
Тогда $angle BRC=2alpha ,$ $angle BCD=angle CRB+angle RBC=90^+2alpha $ как внешний угол треугольника и $angle O_CN=displaystyle fracangle BCD=45^+2alpha $ так как центр вписанной в угол окружности лежит на биссектрисе этого угла.
Из треугольника $O_CN$ находим:
Значит, $BC=BN+NC=displaystyle frac+displaystyle frac=displaystyle frac.$
Аналоично, $angle O_DM=tg(45^-alpha )$ и
$AD=AM+MD=displaystyle frac+displaystyle frac=displaystyle frac.$
Так как $AB=AE+EF+FB=displaystyle frac+displaystyle frac+displaystyle frac=3,$ то $S_=displaystyle fraccdot AB=displaystyle frac<displaystyle frac+displaystyle frac>cdot 3=displaystyle frac.$
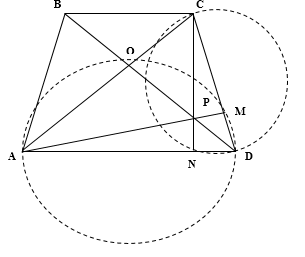
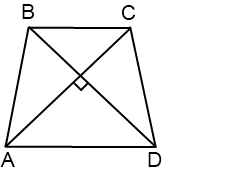
Диагонали равнобедренной трапеции ABCD с основаниями BC и AD перпендикулярны. Окружность с диаметром AD пересекает боковую сторону CD в точке M, а окружность с диаметром CD пересекает основание AD в точке N. Отрезки AM и CN пересекаются в точке P.
а) Докажите, что в четырёхугольник ABCP можно вписать окружность.
б) Найдите радиус этой окружности, если BC = 7, AD = 23.
а) Пусть $O$ — точка пересечения диагоналей трапеции. Так как $AD$ и $CD$ — диаметры окружностей, то $angle AMD=angle CND=90^.$ По условию $ACperp BDRightarrow ACperp BO,$ следовательно , $CN,$ $AM$ и $DO$ — высоты треугольноки $ACD.$ Они пересекаются в одной точке $P.$
Трапеция равнобедренная, а ее диагонали перпендикулярны, поэтому треугольник $BOC$ и $AOD$ — равнобедренные и прямоугольные, следовательно, $angle CBD=angle CAD=45^.$ Так как $ADperp CN,$ то $BCperp CN.$ Значит, в прямоугольных треугольниках $BCP$ и $CAN$ углы при основании равны $45^$ и треугольники являются равнобедренными, поэтому $BC=CP$ и $AN=CN.$
Прямая $CO$ является серединным перпендикуляром к отрезку $BD$. Точка $A$ принадлежит этой прямой, поэтому $AB=AP.$
Тогда верно, что $BC+AP=AB+CP$ (то есть суммы противоположных сторон равны), следовательно, в четырехугольнике $ABCP$ можно вписать окружностью.
б) Так как $N$ — основание высоты в равнобедренной трапеции, то
$DN=displaystyle frac=displaystyle frac=8,$
По теореме Пифагора из треугольника $ACN$ $AC=sqrt<CN^+AN^>=23sqrt.$
Аналогично из треугольника $BCP$ $BP=7sqrt,$ из треугольника $CND$
Выразим площадь четырехугольника $ABCP$ двумя способами:
$S_=displaystyle fracACcdot BPcdot sin 90^=displaystyle fracP_cdot r,$
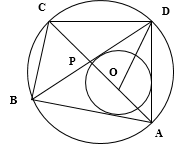
Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекаются в точке P, причём BC = CD.
а) Докажите, что $displaystyle frac=displaystyle frac$.
б) Найдите площадь треугольника COD, где O — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 5, а BC = 5√2.
а) Вписанные углы $BAC$ и $DAC$ равны, как опирающиеся на равные хорды, значит, $AC$ — биссектриса угла $BAD. $
Вписанные углы $ADB$ и $ACB$ опираются на одну и ту же дугу, поэтому они тоже равны. Значит, треугольники $ADP$ и $ACB$ подобные по двум углам. Следовательно, $displaystyle frac=displaystyle frac.$
б) Точки $A$ и $C$ принадлежит окружности с диаметром $BD$, значит, треугольники $ABD$ и $BCD$ прямоугольные. По условию треугольник $BCD$ равнобедренный, поэтому $BD=BCsqrt=10$ и углы при основании равны $45^.$
Катет $AB$ прямоугольного треугольника $ABD$ равен половине гипотенузы $BD,$ следовательно, $angle ADB=30^,angle ABD=60^.$
Так ка центр окружности, вписанной в треугольник, — точка пересечения его биссектрис, то точка $O$ лежит на биссектрисе $AC$ угла $BAD$ и на биссектрисе угла $ADB.$ Тогда $angle ACD=angle ABD=60^$ (как опирающиеся на одну хорду) и $angle ODB=displaystyle fracangle ADB=15^. $ Получаем, что $angle ODC=angle ODB+angle BDC=15^+45^=60^.$
Значит, треугольник $COD$ — равностронний со стороной $5sqrt.$
В ответе необходимо записать полученное значение пункта б), умноженное на √3, то есть 37,5.
Видео:Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.Скачать
Узнать ещё
Знание — сила. Познавательная информация
Видео:Геометрия Трапеция ABCD вписана в окружность с диаметром AD. Найдите высоту трапеции, если радиусСкачать

В равнобедренной трапеции диагонали перпендикулярны
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
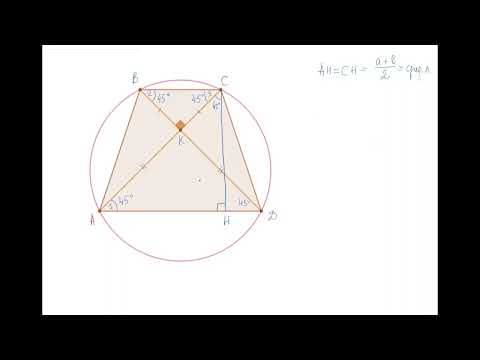
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
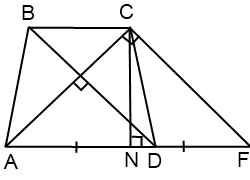
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм ( BC ∥ DF как основания трапеции, BD ∥ CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
sin 90 º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
Видео:В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12.Скачать

Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Видео:№552. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите:Скачать

Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и
, образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и
, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Видео:8 класс, 6 урок, ТрапецияСкачать

Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Видео:Геометрия Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром OСкачать

Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка —
и
, то
Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Площадь
или
где
– средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
💡 Видео
Диагонали трапеции и точка их пересеченияСкачать

Задание 25_Признак равнобедренной трапецииСкачать

Задание 26 Равнобедренная трапеция Окружности, вписанные в треугольникиСкачать

Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать

Геометрия Диагональ равнобокой трапеции перпендикулярна боковой стороне, а угол между большимСкачать

ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

№390. Один из углов равнобедренной трапеции равен 68°. Найдите остальные углыСкачать

Замечательное свойство трапеции | ЕГЭ по математике 2020Скачать

№438. В трапеции ABCD с большим основанием AD диагональ АС перпендикулярна к боковой стороне CDСкачать

№ 501-600 - Геометрия 8 класс МерзлякСкачать

Диагональ равнобокой трапеции перпендикулярна боковой стороне гиа егэ огэ решениеСкачать

Задание второй части реального варианта ЕГЭ 2015 Планиметрия #3Скачать