Диагонали km и ln четырехугольника klmn вписанного в окружность

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Ваш ответ

Видео:3 правила для вписанного четырехугольника #shortsСкачать

решение вопроса

Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,036
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Применение теоремы Вариньона к решению задач

2. 2. Применение теоремы Вариньона к решению задач.

Рассмотрим применение теоремы Вариньона к решению планиметрических задач повышенной трудности. Дело в том, что планиметрические задачи на олимпиадах встречаются значительно чаще.

Мы будем называть параллелограмм KLMN параллелограммом Вариньона, а отрезки КМ и LN, соединяющие середины противоположных сторон четырёхугольника АВСD — средними линиями этого четырёхугольника.

Задача 1. В выпуклом пятиугольнике ABCDE середины сторон AB и CD, BC и DE соединены отрезками. K, L – середины этих отрезков. Доказать, что отрезок KL параллелен пятой стороне AE и составляет ¼ от неё.

Решение: отрежем четырёхугольник ABCD и пусть Р-середина AD, тогда по теореме Вариньона A1B1C1P – параллелограмм, А1С1 – его диагональ и К – середина А1С1, значит, К – середина и второй

диагонали параллелограмма В1Р. Значит, KL – средняя линия треугольника PB1D1, поэтому KL||PD1 и KL=1/2 PD1, но PD1 – средняя линия треугольника ADE, значит, PD1||AE и PD1=1/2AE, поэтому KL||AE и KL=1/4 AE.

Задача 2. Верно ли, что можно составить треугольник из любой средней линии треугольника и отрезков, вдвое меньших его диагоналей?

Решение: верно, так как параллелограмм Вариньона существует для любого выпуклого четырёхугольника. Например, условию задачи удовлетворяют треугольники KLM и LMN на рис. 10. рис. 10

Задача 3. Средние линии четырёхугольника ABCD равны a и b, а угол между ними 60˚. Найдите диагонали четырёхугольника.

Решение: пусть KM=a, LN=b, (рис. 10). Тогда NM=, а LT=.

Из треугольника LTM по теореме косинусов . Но LM= BD, поэтому , откуда BD=. Аналогично из треугольника TNM найдём MN, потом вычислим AC: AC=.

Ответ: ;

Задача 4. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.

Доказательство: в параллелограмме Вариньона, как и в любом другом параллелограмме, сумма квадратов рис. 11 диагоналей равна сумме квадратов всех его сторон, т. е. Учитывая, что KL=1/2 AC и LM= 1/2 BD (рис. 11), получим: KM2+LN2=1/2(AC2+BD2), AC2+BD2=2(KM2+LN2).

Задача 5. Докажите, что площадь параллелограмма Вариньона равна половине площади четырёхугольника ABCD.

Доказательство: (рис. 12).

Учитывая, что , KL=1/2 AC и KN=1/2 BD, получим: рис. 12

.

Задача 6. Докажите, что все четырёхугольники, имеющие общие середины

Доказательство: действительно, для всех таких четырёхугольников определён один и тот же параллелограмм Вариньона. Его площадь равна половине площади каждого из исходных четырёхугольников (задача 5), тем самым их равновеликость доказана.

Задача 7. Докажите, что если диагонали четырёхугольника равны, то его площадь равна произведению средних линий.

Доказательство: в случае равенства диагоналей AC и BD параллелограмм Вариньона KLMN является ромбом (рис. 13), а рис. 13

площадь ромба равна половине произведения диагоналей:

, тогда .

Задача 8. Диагонали четырёхугольника ABCD равны d1 и d2, а средние линии равны между собой. Найдите площадь четырёхугольника.

Решение: из условия задачи следует, что в параллелограмме Вариньона диагонали KM и LN равны (рис. 12). Значит, KLMN – прямоугольник и SKLMN=1/2 d1d2, а с другой стороны, SKLMN=1/2 SABCD, следовательно, SABCD=1/2d1d2.

Ответ: SABCD=1/2d1d2.

Задача 9. Докажите, что площадь четырёхугольника равна произведению средней линии на одну из диагоналей и на синус угла между ними.

Доказательство: согласно рис. 14 необходимо доказать, рис. 14

что . Треугольник KLN представляет собой половину параллелограмма Вариньона. (). Так как KL=1/2AC, то , значит, , а с другой стороны, (см. задачу 8), тогда .

Задача 10. Докажите, что сумма квадратов сторон четырёхугольника равна сумме квадратов его диагоналей, сложенной с учетверённым квадратом отрезка, соединяющего середину его диагоналей.

Доказательство: согласно рис. 11 надо доказать, что. Для медианы ET треугольника ELN имеем: , где , , откуда . Аналогично, выразив медиану FT треугольника KFM и учитывая, что и , получим: .

Кроме того, (задача 7).

Итак, получаем: , откуда:

Задача 11. Постройте трапецию по диагоналям, одному из углов и отрезку, соединяющему середины оснований.

Решение: пусть в трапеции ABCD, которую необходимо построить, известны длины диагоналей AC и BD, отрезка LN и величина угла А (рис. 15).

Поскольку и , нетрудно построить по трём рис. 15

сторонам треугольник KLN. Далее построим его до параллелограмма Вариньона. Затем на отрезке KN построим сегмент, вмещающий угол А, и проведём через точку N параллельно KM прямую, она пересечёт сегмент в точке А. Дальнейшее построение очевидно.

В ходе работы мы прорешали более двадцати пяти задач, формулировки и решения наиболее интересных из них дополнительно приведены в приложении. Мы убедились в том, что теорема Вариньона помогает красиво, оригинально решать задачи, открывать и доказывать новые свойства четырёхугольников.

Видео:Вписанный в окружность четырёхугольник.Скачать

Окружность радиуса 6 вписана в четырехугольник KLMN с диагоналями KM = 14, LN = 24?

Геометрия | 5 — 9 классы

Окружность радиуса 6 вписана в четырехугольник KLMN с диагоналями KM = 14, LN = 24.

Известно, что LM = MN.

Найдите площадь треугольника KLN.

Ответ получается : 12

Видео:Геометрия Теорема Птолемея Произведение диагоналей вписанного в окружность четырехугольника равноСкачать

Прямоугольные треугольник вписан в окружность радиуса 5см?

Прямоугольные треугольник вписан в окружность радиуса 5см.

В треугольник вписана окружность радиуса 1 см.

Найдите площадь треугольника.

Видео:11 класс, 43 урок, Вписанный четырехугольникСкачать

Прямоугольный треугольник вписан в окружность радиуса 5см в треугольник вписана окружность радиуса 1см найдите площадь треугольника?

Прямоугольный треугольник вписан в окружность радиуса 5см в треугольник вписана окружность радиуса 1см найдите площадь треугольника.

Видео:Геометрия Найдите углы четырехугольника MNKP, вписанного в окружность, если угол MKP = 58, угол MPNСкачать

Известны стороны четырехугольника, вписанного в окружность : 3, 4, 5, 6?

Известны стороны четырехугольника, вписанного в окружность : 3, 4, 5, 6.

Найдите его площадь.

Видео:ЕГЭ Задание 16 Признак вписанного четырехугольникаСкачать

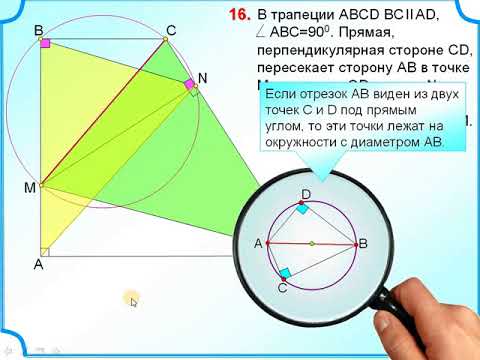
Во вписанном четырехугольнике KLMN стороны LM и MN равны?

Во вписанном четырехугольнике KLMN стороны LM и MN равны.

Окружность Z с центром M касается отрезка LN.

Точка O – центр вписанной окружности треугольника KLN.

Докажите, что прямая, проходящая через O параллельно KL, касается Z.

Видео:Вписанный угол, который опирается на диаметрСкачать

Найдите длину окружности описанной около правильного четырехугольника, если радиус вписанной в этот четырехугольник окружности равен 4см?

Найдите длину окружности описанной около правильного четырехугольника, если радиус вписанной в этот четырехугольник окружности равен 4см.

Видео:ОПИСАННЫЕ И ВПИСАННЫЕ ОКРУЖНОСТИ ЧЕТЫРЕХУГОЛЬНИКА . §10 геометрия 8 классСкачать

Правильный треугольник вписан в окружность, радиуса 6 см ?

Правильный треугольник вписан в окружность, радиуса 6 см .

Найдите периметр треугольника и радиус вписанной в него окружности.

Видео:Вписанные четырехугольники. Метод вспомогательной окружностиСкачать

Радиус окружности равен 6?

Радиус окружности равен 6.

Найдите площадь правильного треугольника, вписанного в эту окружность.

Видео:Вписанный четырёхугольник | ЕГЭ-2018. Задание 16. Математика. Профильный уровень | Борис ТрушинСкачать

Найдите радиус окружности, вписанной в прямоугольный треугольник, если известны радиусы и окружностей, вписанных в два треугольника, на которые высота, проведенная из вершины прямого угла, делит этот ?

Найдите радиус окружности, вписанной в прямоугольный треугольник, если известны радиусы и окружностей, вписанных в два треугольника, на которые высота, проведенная из вершины прямого угла, делит этот треугольник.

Видео:#58. Олимпиадная задача о четырехугольникеСкачать

В окружность с радиусом R, вписан правильный треугольник?

В окружность с радиусом R, вписан правильный треугольник.

Найдите радиус окружности, вписанной в этот треугольник.

Видео:Вписанные и описанные четырехугольники | Дядя Артем | ОГЭ по математикеСкачать

Найдите площадь правильного треугольника, если радиус вписанной в него окружности равен 4?

Найдите площадь правильного треугольника, если радиус вписанной в него окружности равен 4.

Вы открыли страницу вопроса Окружность радиуса 6 вписана в четырехугольник KLMN с диагоналями KM = 14, LN = 24?. Он относится к категории Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Геометрия, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Т. к. Треугл р / б то углы при основании равны(по 40°) значит тупой угол = 180 — (40 + 40) = 100°.

Проведем высоты из вершин В и С Средняя линия = (АD + BC) / 2 = (AE + EF + FD + BC) / 2 Т. К. трапеция равнобедренная, то FD = AE BC = EF Ср. Линия = (AE + EF + AE + EF) / 2 = AE + EF = AF а AF можно найти из треугольника ACF AF = AC / Корень(2) = ..

Решение на фото . Надеюсь всё поймешь.

8. 360 — 230 = 130 — сумма углов А и Д 130 / 2 = 65 — угол С.

Ответ с решением приведён на данном изображении.

Т. к. AB = BC, треугольник равнобедренный, это значит, что угол BAC = углу BCA. Сумма углов в треугольнике = 180. Поэтому BCA + BAC + ABC = 180, но BAC = BCA 2BCA + 148 = 180 2BCA = 180 — 148 2BCA = 32 BCA = 16.

1) 6 * 12 = 72 (м2) — площадь участка 2) 6 * 7 = 42 (м2) — площадь участка, засаженного газонной травой 3) 72 — 42 = 30 (м2) — площадь участка, отведённого под розы.

1) Т. К ∠AOC центральный, то ∪AC = 80° 2) Т. К ∠ABC вписанный, то ∠ABC = 1 / 2∪AC = 40° 3) Доп. Построение : АС Т. К ΔАВС равнобедренный, то ∠BAC = ∠BCA = (180° — 40°) : 2 = 70° Т. К ∠BAC вписанный, то ∪АВ = 2∠ВАС = 70° * 2 = 140° Ответ : ∠АВС =..

Сумма углов треугольника 180° 5 : 1 : 3 Т. Е. всего частей 5 + 1 + 3 = 9 частей 180° : 9 = 20° одна часть Углы треугольника соотносятся как 5 * 20° : 20° : 20° * 3 100° : 20° : 60°.

🎦 Видео

САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

ЧЕТЫРЕХУГОЛЬНИК и ОКРУЖНОСТЬ | ЕГЭ Математика | @matematikajСкачать

Диагонали четырехугольника равны 4 и 5.Скачать

Пробный ЕГЭ 2013 В6 диагональ прямоугольника ABCD #6Скачать

найти сторону четырехугольника, в который вписана окружностьСкачать