Диагональ равнобокой трапеции перпендикулярна боковой стороне найдите радиус окружности

Видео:Геометрия Диагональ равнобокой трапеции перпендикулярна боковой стороне которая равна 15 см НайдитеСкачать

Ваш ответ

Видео:Геометрия Диагональ равнобокой трапеции перпендикулярна боковой стороне, а угол между большимСкачать

решение вопроса

Видео:Геометрия Диагональ равнобокой трапеции перпендикулярна боковой стороне, а меньшее основание равноСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 607,049
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Геометрия Основания равнобокой трапеции равны 9 см и 21 см а высота 8 см Найти радиус окружностиСкачать

Диагональ равнобокой трапеции перпендикулярна боковой стороне найдите радиус окружности

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.^$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям — подобны.

$$ 4.^$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.^$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.^$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.^$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.^$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.^$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.^$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

$$ 4.^$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` — диагональ, `c` — боковая сторона, `a` и `b` основания.

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.^$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.^$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Докажем, например, утверждение $$ 4.^$$ .

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«||«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.^$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` — его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` — её точка пересечения с прямой `BC` (рис. 30б).

По построению `ACKD` — параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`

(т. к. угол `BDK` — это угол между диагоналями трапеции).

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Пусть `BC=a`, `AD=b`, и пусть `h` — высота трапеции (рис. 31). По свойству $$ 4.^$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Трапеция равнобокая, по свойству $$ 4.^$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.^$$

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.^$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

$$ 4.^$$. Если `S_1` и `S_2` — площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.

$$ 4.^$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` — какая-то сторона (или диагональ трапеции), `alpha` — смотрящий на неё вписанный угол.

Видео:Геометрия Диагональ равнобокой трапеции перпендикулярна боковой стороне и образует с основаниемСкачать

Около окружности радиуса корень из 3 описана равнобокая трапеция с большим основанием 6?

Геометрия | 10 — 11 классы

Около окружности радиуса корень из 3 описана равнобокая трапеция с большим основанием 6.

Боковые стороны трапеции продолжены до их пересечения.

Найти длину боковой стороны полученного равнобедренного треугольника.

Прикрепляю решение фотографией.

Видео:Геометрия Диагональ равнобокой трапеции перпендикулярна боковой стороне, которая равна 12 смСкачать

Диагональ равнобедренной трапеции перпендикулярна боковой стороне?

Диагональ равнобедренной трапеции перпендикулярна боковой стороне.

Найдите радиус окружности, описанной около трапеции если диагональ равна 12 см а боковая сторона 9см.

Видео:№438. В трапеции ABCD с большим основанием AD диагональ АС перпендикулярна к боковой стороне CDСкачать

Равнобедренная трапеция с основания 5 и 9 описана около окружности?

Равнобедренная трапеция с основания 5 и 9 описана около окружности.

Найдите боковую сторону трапеции.

Видео:Диагональ равнобокой трапеции перпендикулярна боковой стороне гиа егэ огэ решениеСкачать

Диагональ, боковая сторона и большее основание равнобокой трапеции соответственно равны 40, 13, 51 см?

Диагональ, боковая сторона и большее основание равнобокой трапеции соответственно равны 40, 13, 51 см.

Найти радиус описанной окружности.

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Около равнобокой трапеции, основания которой 7см и 25см, а боковые стороны 15см, описана окружность?

Около равнобокой трапеции, основания которой 7см и 25см, а боковые стороны 15см, описана окружность.

Найти радиус окружности.

Видео:Геометрия Диагональ равнобокой трапеции является биссектрисой ее острого угла и перпендикулярнаСкачать

Диагональ равнобедренной трапеции перпендикулярна боковой стороне?

Диагональ равнобедренной трапеции перпендикулярна боковой стороне.

Найти диагональ трапеции если радиус описанной окружности равен 13см, а боковая сторона 10см.

Видео:Геометрия Диагональ AC равнобокой трапеции ABCD (BC ll AD) равна 8 см угол CAD = 38 угол BAD = 72Скачать

Около окружности описана равнобокая трапеция АВСD?

Около окружности описана равнобокая трапеция АВСD.

Угол между основаниями АD и боковой стороной АВ равен 60 градусов.

Найти боковую сторону и основания трапеции, если радиус окружности равен 4 см.

ПОЖАЛУЙСТА С ОБЪЯСНЕНИЕМ!

Видео:Малоизвестные свойства равнобедренной трапеции. Разбор задачи 17 ЕГЭ профиль.Скачать

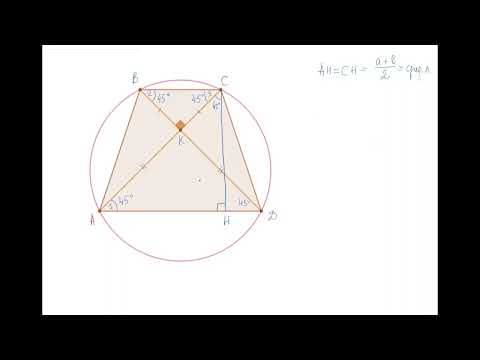
Диагональ, боковая сторона и большее основание равнобедренной трапеции равны соответственно 40, 13, 51 см?

Диагональ, боковая сторона и большее основание равнобедренной трапеции равны соответственно 40, 13, 51 см.

Найдите радиус окружности, описанной около трапеции.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Диагональ равнобедренной трапеции перпендикуляона боковой стороне?

Диагональ равнобедренной трапеции перпендикуляона боковой стороне.

Найдите радиус окружности описанной около трапеции , если диагональ равна 12см , а боковая сторона — 9см.

Видео:8 класс, 6 урок, ТрапецияСкачать

Диагональ равнобедренной трапеции перпендикулярна боковой стороне?

Диагональ равнобедренной трапеции перпендикулярна боковой стороне.

Найдите радиус окружности, описанной около трапеции, если диагональ равна 12 см, а боковая сторона — 9 см Диагональ равнобедренной трапеции перпендикулярна боковой стороне.

Найдите диагональ трапеции, если радиус описанной окружности равен 13 см, а боковая сторона — 10 см.

Видео:Г: Найдите диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12 см, еслиСкачать

Найти радиус окружности описанной около равнобедренной трапеции с основаниями 2 и 14 и боковой стороной 10?

Найти радиус окружности описанной около равнобедренной трапеции с основаниями 2 и 14 и боковой стороной 10.

Вы находитесь на странице вопроса Около окружности радиуса корень из 3 описана равнобокая трапеция с большим основанием 6? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 10 — 11 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Рисунок 3, основание это радиус круга, соответственно диаметр равен 4, а высота 3 она же образующая.

5 + 5 + 7 = 17 (см) ₽ 5 + 5 + 5 = 15(СМ) ₽.

Рассмотрим BKC, КЕ биссектриса т. Е делит угол пополам значит ВКЕ = СКЕ.

Ответ : |BC| = a = 2√3. |2AO + 2CO| = 4. |AС — (3 / 2) * ОС| = 3. Объяснение : В равностороннем треугольнике центр описанной окружности лежит на пересечении высот треугольника, которые являются и биссектрисами и медианами. АО — радиус описанной о..

Привет, BD — выстота = >BDC = 90° найдем угол DBC = 180 — (90 + 42) = 48° Треугольники авd и abd равны = >ABD = 48 ABC = 48 + 48 = 96°.

Пусть A1 — начало координат Ось X — A1B Ось Y — A1D1 Ось Z — A1A A1D1 (0 ; 1 ; 0) M(1 ; 1 ; 0. 5) D(0 ; 1 ; 1) Уравнение A1MD ax + by + cz = 0 подставляем координаты точек a + b + 0. 5c = 0 b + c = 0 Пусть с = — 2 тогда b = 2 a = — 1 — x + 2y — 2z ..

Р = а + в + с (68 — 16) : 2 = 26(см) боковая сторона треугольника.

68 — 16 = 52приходится на две стороны, так как треугольник равнобедренный то стороны равные 52 : 2 = 26 боковая сторона.

36 : 2 = 18 — отрезок КВ 18 : 2 = 9 — отрезок МК.

1) Точки в пл. АДД1 : А , Д Д1 , А1 . Точки в пл. АВС : А , В , С , Д . 2) MS лежит в пл. АВСД МД в пл. АВСД и АА1Д1Д АВ в пл. АВСД и АА1В1В 3) АА1 , ВВ1 , СС1 , ДД1 перпендикулярны пл. АВСД 4) прямой АД параллельны пл. ВВ1С1С и А1В1С1Д1 5) ..

📽️ Видео

№527. В равнобедренной трапеции диагональ равна 10 см, а высота равна 6 см. Найдите площадь трапецииСкачать

№ 501-600 - Геометрия 8 класс МерзлякСкачать

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12.Скачать

Боковая сторона равнобедренной трапеции равна ее меньшему основаниюСкачать

Геометрия Диагональ равнобокой трапеции равна 14 см и образует с основанием угол 60. Найдите среднююСкачать