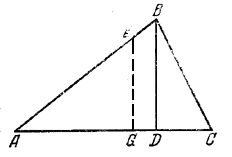
Площади S1 и S2 треугольников ADB и СВD, имеющих общую высоту, относятся как основания, т. е.
Следовательно, S1= 18 /25 S, гдеS = S1 + S2 есть площадь треугольника ABC. По условию прямая EG делит пополам площадь S; значит, эта прямая пересечет основание АС между точками А и D (а не между D и С). Получим треугольник AGE; его площадь S3 равна 1 /2S. Так как площади подобных треугольников AGE и ADB относятся как квадраты сторон AG и AD, то
18 /25 S : 1 /2S = 36 2 : AG 2 .
Видео:Площадь треугольника. Как найти площадь треугольника?Скачать
Медиана делит площадь треугольника пополам
Медиана делит площадь треугольника пополам
Два треугольника называются равновеликими. Если они имеют одинаковую площадь.
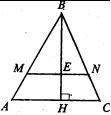
Теорема 1. Медиана делит треугольник на два равновеликих треугольника.
Пусть ВМ – медиана треугольника АВС. Докажем, что
.
Проведем высоту BH треугольника АВС. Тогда
,
.
Так как ВМ – медиана треугольника АВС, то АМ=МС, поэтому
.
,
.
Что и требовалось доказать.
Теорема 2. Медианы треугольника разбивают его на шесть равновеликих треугольников.
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Из теоремы, в частности следует, что если точку пересечения медиан треугольника соединить со всеми его вершинами, то треугольник разобьется на три равновеликие части.
Задача 1 Две медианы треугольника взаимно перпендикулярны и равны соответственно 3 и 4. Найти площадь треугольника.
Пусть в треугольнике АВС медианы АМ и ВЕ равны 3 и 4 соответственно, 
, К – точка пересечения медиан.
,
.
Так как треугольник АВК прямоугольный с прямым углом ВКА, то 
.
Так как медиан делят треугольник на 6 равновеликих частей, то 
.
Задача 2 Медианы треугольника равны 6, 8 и 10, найти площадь треугольника.
Пусть медианы АM, BE и CD данного треугольника соответственно равны 6, 8 и 10, К – точка их пересечения. Отложим на продолжении луча ВЕ за точку Е отрезок EF=KE. Соединим точки С, F и A.
Рассмотрим треугольник KAF.
,
то 
.
Далее, 
, так как CKAE – параллелограмм (по признаку параллелограмма: ели диагонали четырехугольника делятся точкой пересечения пополам, до данный четырехугольник параллелограмм), получаем 
.
Так как 
, то есть 
, то по обратной теореме Пифагора (если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный) треугольник KAF – прямоугольный и 
.
Вычислим площадь треугольника AKF:
.
Теперь сравним площади треугольников AKF и АВС: так как AE – медиана треугольника AKF, то
, 
,
.
.
Отметим, что задачу можно решить по-другому, если воспользоваться тем фактом, что:
площадь треугольника, образованного медианами данного треугольника составляет 
от площади самого треугольника.
Доказательство можно посмотреть, например, в методическом пособии «Опорные задачи по планиметрии».
Вопросы для самопроверки:
1. Какие треугольники называются равновеликими?
2. Площадь треугольника равна S. Чему равна площадь каждого из треугольников, на которые его разбивает медиана, проведенная к какой-либо стороне этого треугольника?
3. На сколько равновеликих частей разбивают треугольник проведенные в нем три медианы?
4. Площадь треугольника равна S. Цент тяжести этого треугольника соединили с его вершинами. Чему равна площадь каждого из получившихся треугольников?
5. Площадь треугольника равна 48, чему равна площадь треугольника, составленного из медиан этого треугольника?
6. Площадь треугольника, составленного из медиан некоторого треугольника равна 24, чему равна площадь треугольника?
Задачи для самостоятельного решения:
1. Две медианы треугольника взаимно перпендикулярны и равны соответственно 6 и 8. Найти площадь треугольника.
2. Медианы треугольника равны 3, 4 и 5 найти площадь треугольника.
3. Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку М пересечения медиан треугольника с вершинами треугольника. Найти площадь треугольника ВМС.
4. Две стороны треугольника равны 10 и 12, а медиана, проведённая к третьей, равна 5. Найдите площадь треугольника.
Видео:Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать
№ 51. Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна А.
Решебник по геометрии за 9 класс (А.В.Погорелов, 2001 год),
задача №51
к главе «§14. Площади фигур».
Выделите её мышкой и нажмите CTRL + ENTER
Большое спасибо всем, кто помогает делать сайт лучше! =)
Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.
🔥 Видео
Биссектриса прямого угла делит медиану пополам! Найти площадь треугольника.Скачать
Площади | Задачи 1-8 | Решение задач | Волчкевич | Уроки геометрии 7-8 классыСкачать
Высота, биссектриса, медиана. 7 класс.Скачать
8 класс, 14 урок, Площадь треугольникаСкачать
Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать
Как найти площадь треугольника без формулы?Скачать
Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать
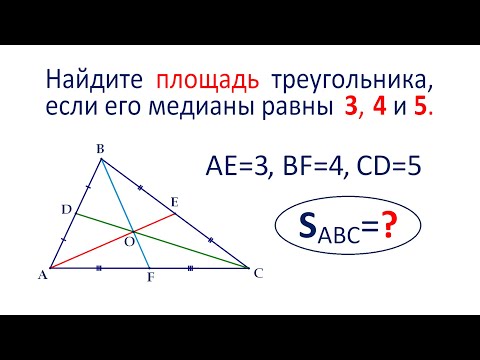
Найдите площадь треугольника, если его медианы равны 3, 4 и 5Скачать
Геометрия Длина основания треугольника равна 36 см. Прямая, параллельная основанию, делит площадьСкачать
Задача по геометрии № 25 ОГЭ на отношение площадейСкачать
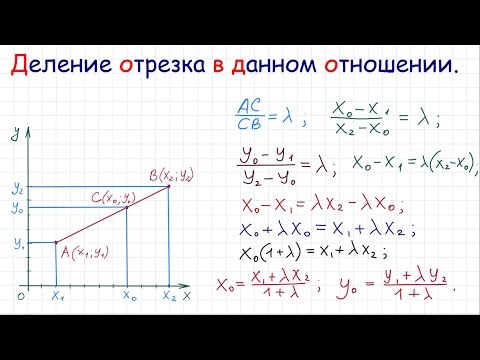
Деление отрезка в данном отношенииСкачать
найти площадь треугольника. Формула Герона. Известны 3 стороны.Скачать
Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать
ВЫСОТА ПРЯМОУГОЛЬНОГО ДЕЛИТ БИССЕКТРИСУ НА ОТРЕЗКИ 9 И 6! Найти площадь.Скачать
Площади треугольникаСкачать
КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать
ПЛОЩАДЬ ТРЕУГОЛЬНИКА формула 9 класс геометрия АтанасянСкачать
Задача из ОГЭ на площадь треугольника #математика #огэматематика #огэ #семенСкачать
