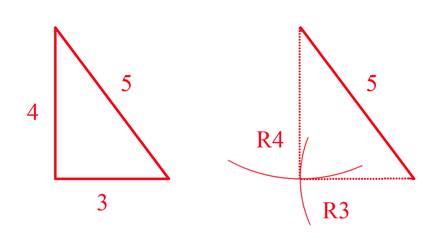Деление отрезка пополам окружности (5 видео)

Деление отрезка пополам при помощи циркуля

Имеется отрезок произвольной длины. Необходимо разделить его пополам, пользуясь только циркулем и не прибегая к помощи линейки.

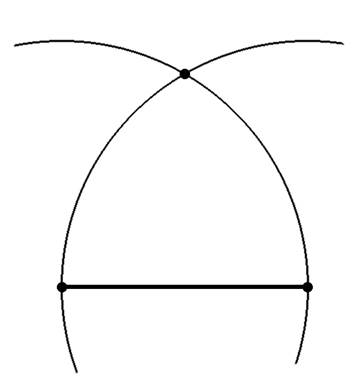
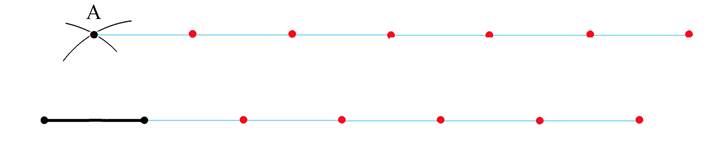
По сути, всё, что можно сделать сначала – это прочертить

Из концов отрезка две окружности радиусом равным длине отрезка.

Концы отрезка и точка пересечения окружностей образуют

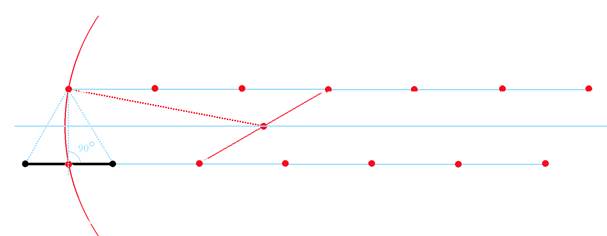
Пользуясь этим методом можно построить сетку из вспомогательных точек сколь угодно большого размера. Нам потребуется всего два ряда точек лежащие на прямой, являющейся продолжением отрезка и параллельной ей прямой проходящей через вершину построенного нами первого треугольника.

В равностороннем треугольнике любая высота (перпендикуляр, проведенный из вершины к противоположной стороне) является одновременно медианой (линией соединяющей вершину и середину противоположной стороны) а значит, чтобы получить

середину отрезка, достаточно провести через вершину треугольника окружность, центр которой лежит на прямой, равноудаленной от прямой, являющейся продолжением исходного отрезка и параллельной ей прямой проходящей через вершину треугольника. Центром окружности может служить середина отрезка, концы которого расположены на вышеупомянутых прямых

Но, по условию задачи, пользоваться линейкой мы не можем

(все линии на рисунках начерчены лишь для пояснения), а значит

в окончательном построении нам придется пользоваться лишь точками из верхнего и нижнего рядов или точкой из верхнего ряда и точкой лежащей на исходном отрезке. Концы вспомогательного отрезка соединить линией мы тоже не сможем, поэтому его центр нам придется получать тоже с помощью единственно циркуля.

Тут нам на помощь придет теорема Пифагора, а точнее её частный случай со сторонами треугольника 3,4 и 5.Угол между сторонами

3 и 4 – прямой, и, следовательно, если мы возьмем отрезок, равный

5 и из одного конца прочертим окружность радиусом 3, а из другого радиусом 4, получим прямоугольный треугольник.

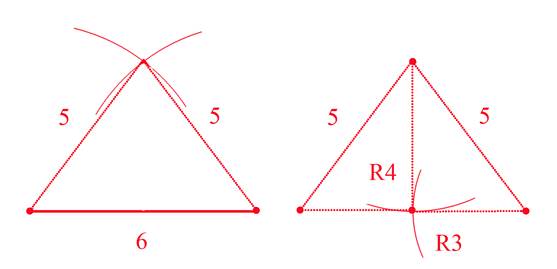
И как следствие мы можем, зная это, получить середину отрезка длиной 6, пользуясь только циркулем.

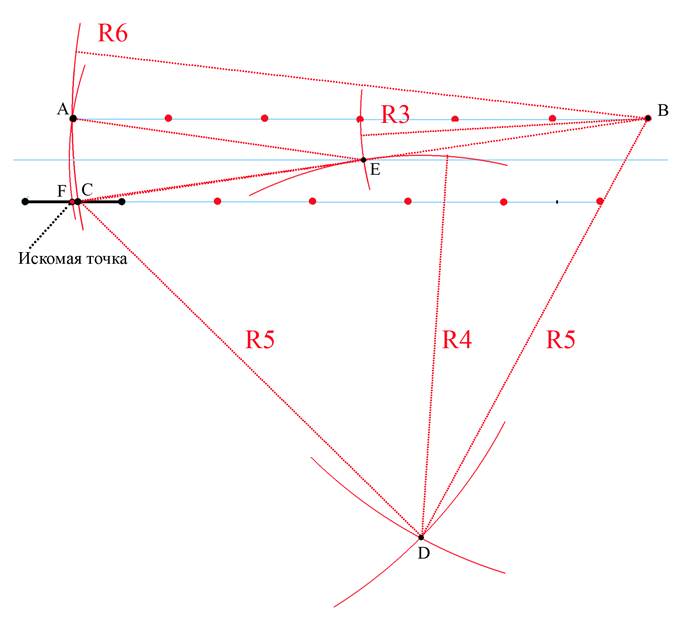
Применив эти построения к нашему случаю, получим такую методу:

1.Проведя из концов исходного отрезка дуги окружностей радиусом

равным длине отрезка получим на их пересечении точку A– вершину равностороннего треугольника.

2.Сходным образом построим два ряда точек, обозначенных на

рисунке красным. Расстояние между двумя соседними точками равно длине исходного отрезка – условной единице. Точки верхнего ряда лежат на одной прямой и нижнего ряда – аналогично.

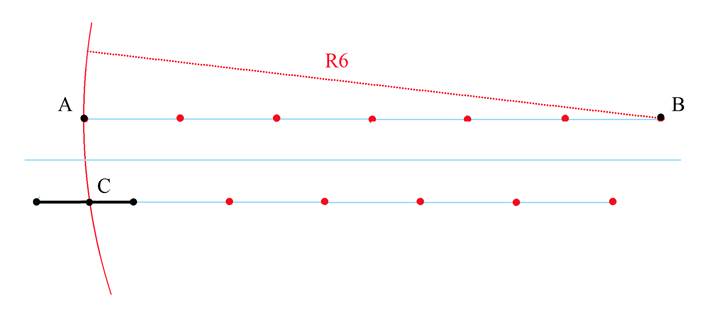
3.Отсчитав от точки А шестую точку, обозначим ее B.

Из точки B проведем дугу окружности радиусом BA= 6

На пересечении этой дуги с исходным отрезком отметим точку C.

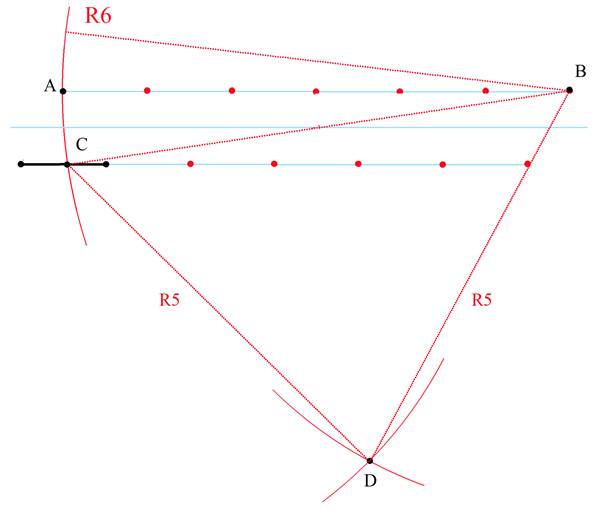
4.Отложим от точки В пять точек и этим радиусом проведем дугу окружности. Этим же радиусом проведем дугу из точки С.

Точку пересечения этих дуг обозначим D.

DC=DB, треугольник CDB – равнобедренный

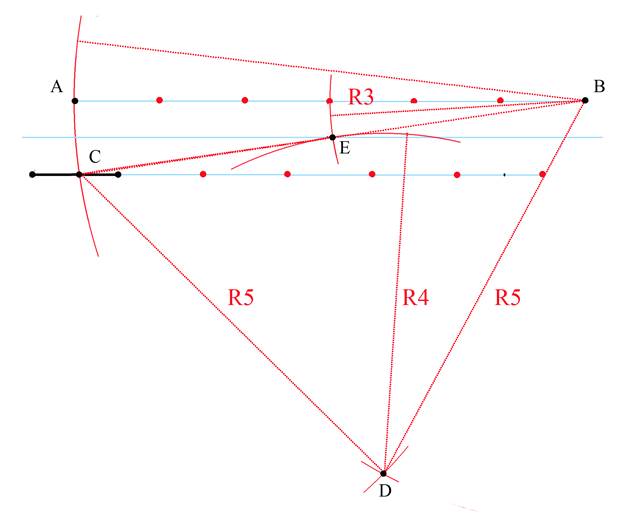
5. Из точки В проведем дугу радиусом 3 а из точки D радиусом 4.

На пересечении дуг получим точку Е – середину отрезка ВС.

Как мы ранее обосновали, точка Е, являясь серединой отрезка ВС,

(как следствие теоремы Пифагора), лежит на прямой , равноудаленной от прямой, являющейся продолжением исходного отрезка и параллельной ей прямой, проходящей через точку А,

а значит равноудалена от точки А и искомой точки, являющейся серединой исходного отрезка. Следовательно, приняв ее за центр

и проведя окружность через точку А, на пересечении этой окружности с исходным отрезком получим искомую точку.

6. Что мы и сделаем.

Точка F и есть искомая точка – середина исходного отрезка

Таким образом, задача деления отрезка пополам решается при помощи одного лишь циркуля.

Это станет видно, когда мы уберем из рисунка вспомогательные лини, с помощью которых иллюстрировалось объяснение и

покажем окружности, использовавшиеся для построения промежуточных точек, ранее не показанные, чтобы не отвлекать от объяснения.

Содержание

Учебно-методическое пособие «Техника выполнения геометрических построений» для выполнения графических работ
1. Деление отрезков и углов
1.1. Деление отрезка пополам
1.2. Деление отрезка на n равных частей
1.3. Деление угла пополам
2. Деление окружности на равные части и построение правильных многоугольников
2.1. Деление окружности на три равные части
2.2. Деление окружности на шесть равных частей
2.3. Деление окружности на пять равных частей
2.4. Деление окружности на семь равных частей
Литература
Деление отрезка
Задачи на построение
📸 Видео

Видео:7 класс - Геометрия - Задачи на построение. Окружность. Деление отрезка пополам.Скачать

Учебно-методическое пособие «Техника выполнения геометрических построений» для выполнения графических работ

При изучении дисциплины «Начертательная геометрия и инженерная графика» студенты должны усвоить правила и последовательность выполнения геометрических построений и сопряжений.

В этом отношении лучшим способом приобретения навыков построения являются задания по вычерчиванию контуров сложных деталей.

Прежде чем приступить к выполнению контрольного задания, нужно изучить технику выполнения геометрических построений и сопряжений по методическому пособию.

Видео:Деление отрезка на 2,4,8 равных частей с помощью циркуля и линейкиСкачать

1. Деление отрезков и углов

Видео:Деление отрезка пополамСкачать

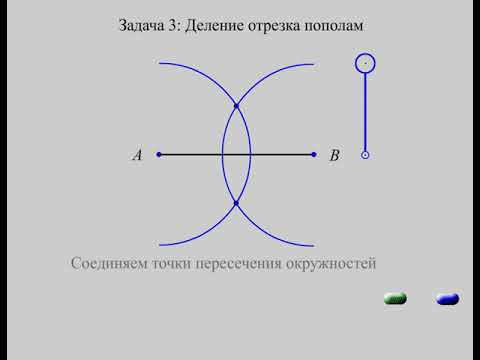
1.1. Деление отрезка пополам

Разделить заданный отрезок АВ пополам.

Из концов отрезка АВ, как из центров, проведем дуги окружностей радиусом R, размер которого должен быть несколько больше, чем половина отрезка АВ (Рис. 1). Эти дуги пересекутся в точках M и N, найдем точку С, в которой пересекаются прямые АВ и MN. Точка С разделит отрезок АВ на две равные части.

Примечание. Все необходимые построения должны и могут выполняться только с помощью циркуля и линейки (без делений).

Видео:Деление отрезка пополамСкачать

1.2. Деление отрезка на n равных частей

Разделить заданный отрезок на n равных частей.

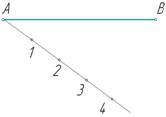
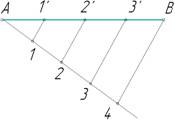
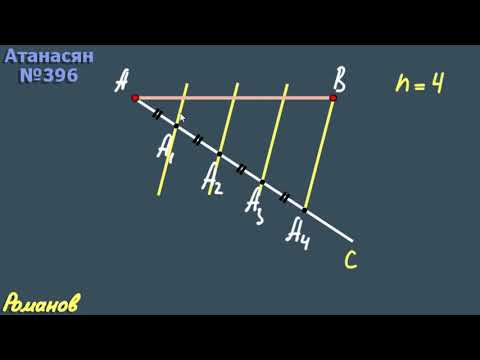
Из конца отрезка – точки А проведем вспомогательный луч под произвольным углом α.(рис.2 а) На этом луче отложим 4 равных отрезка произвольной длины (рис.2б). Конец последнего, четвертого, отрезка (точку 4) соединим с точкой В. Далее из всех предыдущих точек 1…3 проведем отрезки, параллельные отрезку В4 до пересечения с отрезком АВ в точках1′, 2′, 3′. Полученные таким образом точки разделили отрезок на равные четыре отрезка

Видео:Деление отрезка в данном отношенииСкачать

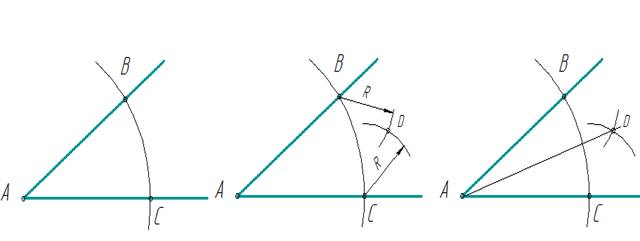
1.3. Деление угла пополам

Разделить заданный угол ВАС пополам.

Из вершины угла А произвольным радиусом проводим дугу до пересечения со сторонами угла в точках В и С (рис.3 а). Затем из точек В и С проводим две дуги радиусом, большим половины расстояния ВС, до их пересечения в точке D (рис.3 б). Соединив точки А и D прямой, получаем биссектрису угла, которая делит заданный угол пополам (рис.3 в)

Видео:ДЕЛЕНИЕ ОТРЕЗКА ПОПОЛАМ С ПОМОЩЬЮ ЦИРКУЛЯ И ЛИНЕЙКИ (БАЗОВАЯ ЗАДАЧА). ЗАДАЧИ | ГЕОМЕТРИЯ 7 классСкачать

2. Деление окружности на равные части и построение правильных многоугольников

Видео:Методы деления отрезка пополам и золотого сеченияСкачать

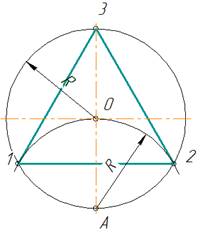
2.1. Деление окружности на три равные части

Из конца диаметра, например, точки А (рис.4) проводят дугу радиусом R, равным радиусу заданной окружности. Получают первое и второе деление – точки 1 и 2. Третье деление точка 3, находится на противоположном конце того же диаметра. Соединив точки 1,2,3 хордами, получают правильный вписанный треугольник.

Видео:Деление отрезка на равные части, перпендикуляр к прямой.Урок 4.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

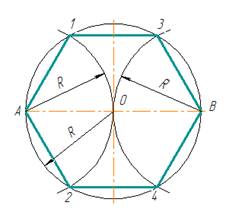
2.2. Деление окружности на шесть равных частей

Из концов какого-либо диаметра, например АВ (рис.5), описывают дуги радиусом R окружности. Точки А, 1,3,В,4,2 делят окружность на шесть равных частей. Соединив их хордами, получают правильный вписанный шестиугольник.

Примечание. Вспомогательные дуги проводить полностью не следует, достаточно сделать засечки на окружности.

Видео:Деление отрезка пополамСкачать

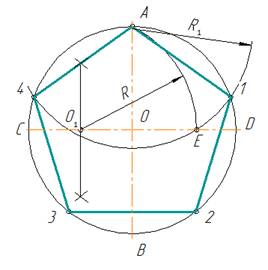
2.3. Деление окружности на пять равных частей

Проводят два взаимно перпендикулярных диаметра АВ и CD (рис.6). Радиус ОС в точке О₁делят пополам.
Из точки О1, как из центра, проводят дугу радиусом О1А до пересечения ее с диаметром CD в точке Е.
Отрезок АЕ равен стороне правильного вписанного пятиугольника, а отрезок ОЕ – стороне правильного вписанного десятиугольника.
Приняв точку А за центр, дугой радиуса R1 = АЕ на окружности отмечают точки 1 и 4. Из точек 1 и 4, как из центров, дугами того же радиуса R1 отмечают точки 3 и 2. Точки А, 1, 2, 3, 4 делятокружность на пять равных частей.

Видео:Деление отрезка пополамСкачать

2.4. Деление окружности на семь равных частей

Из конца диаметра, например, точки А проводят дугу радиуса R, равного радиусу окружности (рис.7). Хорда CD равна стороне правильного вписанного треугольника. Половина хорды CD с достаточным приближением равняется стороне правильного вписанного семиугольника, т.е. делит окружность на семь равных частей.

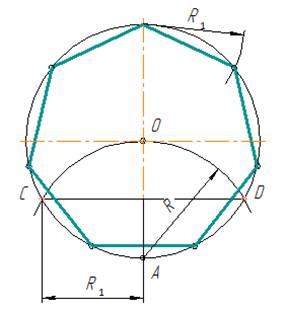
Рис. 7

Видео:Построение серединного перпендикуляра. Деление отрезка пополамСкачать

Литература

Боголюбов С.К. Инженерная графика: Учебник для средних специальных учебных заведений. – 3-е изд., испр. И доп. — М.: Машиностроение, 2006. – с.392: ил.
Куприков М.Ю. Инженерная графика: учебник для ССУЗов – М.: Дрофа, 2010 – 495 с.: ил.
Федоренко В.А., Шошин А.И. Справочник по машиностроительному черчению Л.: Машиностроение. 1976. 336 с.

Поддержка
(495) 589-87-71

Сервис «Комментарии» — это возможность для всех наших читателей дополнить опубликованный на сайте материал фактами или выразить свое мнение по затрагиваемой материалом теме.

Редакция Информио.ру оставляет за собой право удалить комментарий пользователя без предупреждения и объяснения причин. Однако этого, скорее всего, не произойдет, если Вы будете придерживаться следующих правил:

Не стоит размещать бессодержательные сообщения, не несущие смысловой нагрузки.
Не разрешается публикация комментариев, написанных полностью или частично в режиме Caps Lock (Заглавными буквами). Запрещается использование нецензурных выражений и ругательств, способных оскорбить честь и достоинство, а также национальные и религиозные чувства людей (на любом языке, в любой кодировке, в любой части сообщения — заголовке, тексте, подписи и пр.)
Запрещается пропаганда употребления наркотиков и спиртных напитков. Например, обсуждать преимущества употребления того или иного вида наркотиков; утверждать, что они якобы безвредны для здоровья.
Запрещается обсуждать способы изготовления, а также места и способы распространения наркотиков, оружия и взрывчатых веществ.
Запрещается размещение сообщений, направленных на разжигание социальной, национальной, половой и религиозной ненависти и нетерпимости в любых формах.
Запрещается размещение сообщений, прямо либо косвенно призывающих к нарушению законодательства РФ. Например: не платить налоги, не служить в армии, саботировать работу городских служб и т.д.
Запрещается использование в качестве аватара фотографии эротического характера, изображения с зарегистрированным товарным знаком и фотоснимки с узнаваемым изображением известных людей. Редакция оставляет за собой право удалять аватары без предупреждения и объяснения причин.
Запрещается публикация комментариев, содержащих личные оскорбления собеседника по форуму, комментатора, чье мнение приводится в статье, а также журналиста.

Претензии к качеству материалов, заголовкам, работе журналистов и СМИ в целом присылайте на адрес

Информация доступна только для зарегистрированных пользователей.

Уважаемые коллеги. Убедительная просьба быть внимательнее при оформлении заявки. На основании заполненной формы оформляется электронное свидетельство. В случае неверно указанных данных организация ответственности не несёт.

Видео:Высота, биссектриса, медиана. 7 класс.Скачать

Деление отрезка

Видео:Построение угла, равного данному. 7 класс.Скачать

Задачи на построение

Деление отрезка пополам

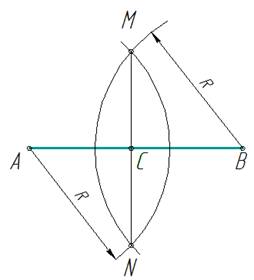
Деление отрезка пополам выполняется следующим образом. На отрезке AB необходимо, из точки А, отложить дугу большую половине этого отрезка. Далее, не меняя значения циркуля, из точки В построим засечки, пересекающие нашу дугу. Пересечение дуги и засечек образуют точки E и D, затем проводим прямую через эти точки, которая и поделит наш отрезок АВ ровно на две части. Если продолжить деление полученных частей пополам можно таким же способом разделить отрезок на 4, 8, 16 и т.д., т.е. на число кратное 2.

Соединим точки Е и D с концами отрезка AB. По построению AD = AE = DB = EB. Поэтому равнобедренные треугольники DAE и DBE равны по трем сторонам. Отсюда следует равенство углов ADO и BDO. В равнобедренном треугольнике ABD, DO- биссектриса, проведенная к основанию, следовательно, она медиана и высота. Отсюда AO = OB, и точка O — середина отрезка AB.

Деление отрезка прямой на пропорциональные части

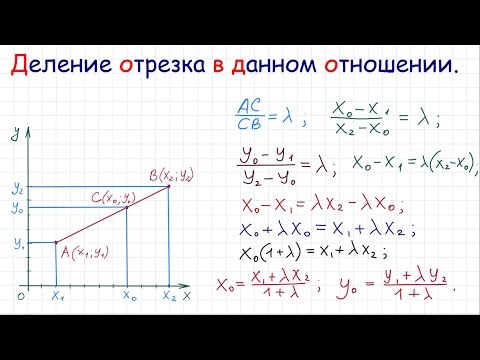
Существует теорема Фалеса, которая звучит следующим образом: «если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки». Используя данную теорему мы можем произвести деление отрезка прямой на пропорциональные части. Разберем как выполняется данное деление.

Для того чтобы разделить отрезок АВ в соотношении например 3:2 (отсчитывая от точки А), необходимо под произвольным углом из точки А провести вспомогательную прямую. Затем на этой прямой отложить 5 произвольных, но равных между собой отрезков. Далее соединить прямой точки В и 5 и из точки 3 параллельно прямой В5 провести прямую до пересечения ее с отрезком АВ, полученная точка пересечения D разделит отрезок АВ в соотношении 3:2. Мы получим отношение AD:DB = 3:2

Рассмотрим треугольники АСВ и AEB. Данные треугольники подобны по двум углам (?A- общий, ?ACD=?AEB- соответственные). Следовательно, отношения сторон треугольников равны. По построению =, значит и =. Значит, отрезок АВ поделен в заданном отношении.

Деление отрезка в крайнем и среднем отношении

На рисунке отрезок АО разделен так, что отношение отрезка АО к отрезку АК равно отношению отрезка АК к отрезку КО (АО : АК=АК : КО). Такое деление известно под названием золотое сечение или золотое отношение. Правило золотого сечения получило популярность благодаря своим применениям в живописи и, особенно, в архитектуре, а также обнаружению этой пропорции (и тесно связанных с ней чисел Фибоначчи) в живой природе.

Графическое построение золотого сечения выполняется следующим образом: отрезок АО делим на две равные части (точка С); в точке О строим перпендикуляр к отрезку АО, на перпендикуляре откладываем отрезок ОМ который равен отрезку ОС; точки А и М соединяют прямой. Далее на этой прямой от точки М откладывают отрезок MN = ОМ и на отрезке АО от точки А откладывают отрезок АК из точки N. Точка К и будет являться результирующей точкой которая делит отрезок АО в крайнем и среднем отношении.