Содержание

Глава 3. Некоторые геометрические построения
§ 16. Деление окружности
Инженерная графика
Практические задания по инженерной графике
Деление окружности на равные части
Графическая работа № 2
Рекомендации по выполнению работы
Инженерная графика деление окружностей на
§ 16. Деление окружности
Инженерная графика
Практические задания по инженерной графике
Деление окружности на равные части
Графическая работа № 2
Рекомендации по выполнению работы
Деление окружности на равные части с примерами и образцами выполнения
Деление окружности на пять, десять и семь равных частей
💥 Видео

Глава 3. Некоторые геометрические построения

Глава 3Общие сведенияДеление отрезка прямойДеление окружностиСкругление угловСопряжение дуг окружностей прямой линиейСопряжение дуг окружностей третьей дугойСопряжение дуги окружности и прямой линии второй дугойОвалыЛекальные кривыеВопросы

Видео:Деление окружностей на равные частиСкачать

§ 16. Деление окружности

Чтобы разделить окружность на четыре равных части , проводят два взаимно перпендикулярных диаметра: на пересечении их с окружностью получаем точки, разделяющие окружность на четыре равные части (рис. 31, а).

Чтобы разделить окружность на восемь равных частей , дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 31, б).

Чтобы разделить окружность на двенадцать равных частей , ее делят на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D и разделяют окружность на двенадцать равных частей (рис. 31, в). Пользуясь радиусом, нетрудно разделить окружность на 3 и 6 равных участков.

Деление окружности на пять и десять равных частей (рис. 31, г). Проведя два взаимно перпендикулярных диаметра AB и CD, делят радиус 0D пополам в точке Е; из точки Е как из центра проводят дугу радиусом АЕ до пересечения ее с диаметром CD в точке F. Отрезок AF равен стороне вписанного пятиугольника, т.е. делят окружность на пять равных частей. Отрезок 0F равняется стороне десятиугольника и делит окружность на десять равных частей.

Другой способ деления окружности на пять и десять равных частей показан на рис. 31,е. Делят радиус, например ОС, пополам в точке D и проводят прямую DB. Откладывают на ней от точки D отрезок DE=D0. Тогда BE равняется стороне десятиугольника, а хорда KL — стороне пятиугольника.

Деление окружности на семь равных частей (рис.31,ж). Проводится вспомогательная дуга радиусом R, определяющая хорду MN, равную стороне правильного вписанного треугольника. Половина хорды MN=R₁ с достаточным приближением равняется стороне правильного вписанного семиугольника, т.е. делит окружность на семь равных частей.

Видео:Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Инженерная графика

Практические задания по инженерной графике

Видео:Деление окружности на равные частиСкачать

Деление окружности на равные части

Графическая работа № 2

Графическая работа № 2, рекомендуемая для выполнения обучающимися инженерной графике, имеет целью освоение навыков вычерчивания окружности, деления ее на равные части и выполнение чертежа контура детали с помощью изученных приемов деления окружности.
В процессе выполнения работы обучающийся должен выполнить рамку чертежа, построить несколько окружностей произвольного радиуса и разбить их при помощи циркуля и линейки на 3, 4, 5, 6, 7 и 8 равных частей (по усмотрению преподавателя это задание может быть выполнено, также, треугольником) .
Второе задание Графической работы №2 заключается в выполнении чертежа детали, контуры которой требуют при вычерчивании использование приемов деления окружности на равные части.
Образец выполнения Графической работы №2 представлен на рисунке ниже.

Для использования образца выполнения Графической работы №2 в качестве раздаточного материала на уроке, его можно скачать здесь.

Работа выполняется на чертежной бумаге формата А4 (297×210 мм). Размещение листа во может быть альбомным или книжным (по усмотрению студента, выполняющего работу) .

Рекомендации по выполнению работы

Выполнение работы следует начинать с определения масштаба изображения, разметки листа и вычерчивания осевых линий для окружностей и симметричных элементов, чтобы обеспечить гармоничность и наглядность работы.
Масштаб изображения подбирается из стандартного ряда таким образом, чтобы поле чертежного листа было заполнено не менее, чем на 60%.
Осевые (штрихпунктирные) линии являются базовыми — они являются исходными элементами для определения положения других линий контура на чертеже. Осевая линия должна пересекаться в центре окружности только штрихами; заканчивается она тоже не точками, а только штрихами. Осевые линии удалять во время выполнения задания, а также по окончании работы нельзя — они являются необходимым элементом любого чертежа.

При делении окружностей на равные части вспомогательные линии и элементы необходимо выполнять тонкими линиями с помощью твердого карандаша (Т или 2Т) .
После выполнения построений вспомогательные линии удалять не следует!

При выполнении первого задания — деление окружности на равные части циркулем, необходимо внимательно ознакомиться с порядком выполнения построений, который подробно представлен на образце Графической работы (см. рисунок внизу) .

Деление окружности на 4 части осуществляется по точкам пересечения с осевыми линиями. При делении на 8 частей необходимо вспомнить прием деления отрезка прямой с помощью циркуля пополам, известный из средней школы, и разделить отрезки (стороны квадрата), полученные при делении окружности на 4 части (см. рис. 1) . При этом все стороны квадрата делить пополам не обязательно — достаточно разделить лишь две соседние стороны, и полученные точки соединить через центр окружности до противоположной стороны.

Деление окружности на 6 частей осуществляется с использованием приема, основанного на том, что по длине окружности можно уложить 6 радиусов этой окружности. Т. е. тем же раствором циркуля, которым вычерчивалась окружность, следует отложить на ней 6 последовательных отрезков. Соединив полученные точки между собой, получим правильный шестиугольник, а если соединить точки через одну, получим правильный треугольник, т. е. разобьем таким образом окружность на три равные дуги.

Некоторую сложность может вызвать деление окружности на 5 и 7 равных частей. Построения здесь выполняются в два этапа: сначала с помощью циркуля определяют длину отрезка, который будет делить окружность на соответствующее количество равных дуг (5 или 7) . Порядок определения длины этих отрезков изображен на левой окружности (перед красной стрелкой), а на правой окружности показан результат деления с помощью полученного отрезка.

При выполнении Графической работы №2 следует обратить внимание на соответствие толщины линий чертежа требованиям ГОСТ, а также на одинаковую толщину одноименных линий чертежа.
На результаты оценивания работы влияют, также, опрятность выполнения работы и гармоничность размещения отдельных изображений и видов на поле листа — необходимо соблюдать требуемые отступы между изображениями и рамкой; поле листа чертежа должно быть использовано на 60. 75%.

Скачать образец работы для последующей печати и использования в качестве раздаточного материала можно здесь.

Для устойчивого закрепления практических навыков деления окружности на равные части, рекомендуется выполнить Графическую работу № 2а, которую можно скачать или распечатать здесь.

Видео:1 2 2 деление окружности на 5 равных частейСкачать

Инженерная графика деление окружностей на

Видео:1 2 1 деление окружностиСкачать

§ 16. Деление окружности

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Инженерная графика

Практические задания по инженерной графике

Видео:Деление окружности на n- равные частиСкачать

Деление окружности на равные части

Графическая работа № 2

Деление окружности на равные части с примерами и образцами выполнения

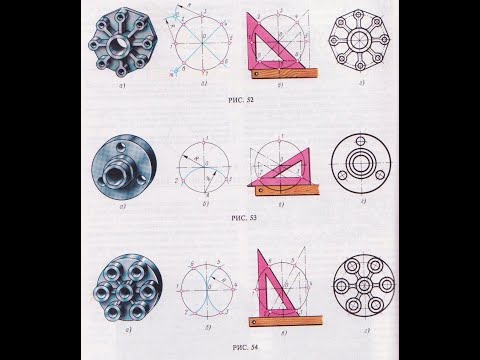
Некоторые детали имеют элементы, равномерно расположенные по окружности, например, детали на рис. 52. 59. При выполнении чертежей подобных деталей необходимо уметь делить окружность на равные части.

Деление окружности на четыре и восемь равных частей. На рис. 52, а показана крышка, в которой имеется восемь отверстий, равномерно расположенных по окружности. При построении чертежа контура крышки (рис. 52, г) необходимо разделить окружность на восемь равных частей.

Два взаимно перпендикулярных диаметра окружности делят ее на четыре равные части (точки 1. 3, 5. 7 на рис. 52. б). Чтобы разделить окруж- ность на восемь равных частей, применяют известный прием деления прямого угла с помощью циркуля на две равные части. Получают точки 2. 4, 6, 8. Это можно сделать с помощью угольника с углами 45 0 (рис. 52, в), гипотенуза угольника должна проходить через центр окружности, или построением.

Деление окружности на три, шесть и двенадцать равных частей. Во фланце (рис. 53, а) имеется три отверстия, равномерно расположенных по окружности. При выполнении чертежа контура фланца (рис. 53, г) нужно разделить окружность на три равные части.

Для нахождения точек, делящих окружность радиуса В на три равные части, достаточно из любой точки окружности, например точки А, провести дугу радиусом В. Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет находиться на пересечении оси окружности, проведенной из точки А, с окружностью (рис. 53, б).

Разделить окружность на три равные части можно также угольником с углами 30 и 60” (рис. 53. в), гипотенуза угольника должна проходить через центр окружности.

На рис. 54, б показано деление окружности циркулем на шесть равных частей. В этом случае выполняется то же нестроение, что на рис. 53, б, но дугу описывают не один, а два раза, из точек 1 и 4 радиусом R, равным радиусу окружности.

Разделить окружность на шесть равных часто! можно и угольником с углами 30 и 60” (рис. 54, в). На рис. 54, а показана крыш ка, при выполнении чертежа которой необходимо выполнить деление окружности на шесть частей.

Чтобы выполнить чертеж детали (рис. 55, а), которая имеет 12 отверстий, равномерно расположенных по окружности, нужно разделить окружность на 12 равных частей (рис. 55, г).

При делении окружности на 12 равных частей с помощью циркуля можно использовать тот же прием, что и при делении окружности на шесть равных частей (рис. 54, б), но дуги радиусом В описывать четыре раза из точек 1, 7, 4 и 10 (рис. 55, б).

Используя угольник с углами 30 и 60 0 с последующим поворотом его на 180 0 . делят окружность на 12 равных частей (рис. 55, в).

Видео:Видеоуроки по КОМПАС 3D. Урок 1 Деление окружности на равные частиСкачать

Деление окружности на пять, десять и семь равных частей

В плашке (рис. 56, а) имеется пять отверстий, равномерно расположенных по окружности. Выполняя чертеж плашки (рис. 56, в), необходимо разделить окружность на пять равных частей. Через намеченный центр О (рис. 56, б) с помощью рейсшины и угольника проводят осевые линии и из точки О циркулем описывают окружность заданного диаметра. Из точки А радиусом R, равным радиусу данной окружности, проводят дугу, которая пересечет окружность в точке n. Из точки n опускают перпендикуляр на горизонтальную осевую линию, получают точку С. Из точки С радиусом R₁ равным расстоянию от точки С до точки 1, проводят дугу, которая пересечет горизонтальную осевую линию в точке т. Из точки 1 радиусом R₂, равным расстоянию от точки 1 до точки т, проводят дугу, пересекающую окружность в точке 2. Дуга 12 является 1/5 длины окружности. Точки 3, 4 и 5 находят, откладывая циркулем отрезки, равные m1.

Деталь ’’звездочка” (рис. 57, а) имеет 10 одинаковых элементов, равномерно расположенных по окружности. Чтобы выполнить чертеж звездочки (рис. 57, в), следует окружность разделить на 10 равных частей. В этом случае следует применить то же построение, что и при делении окружности на пять частей (см. рис. 56, б). Отрезок п₁ будет равняться хорде, которая делит окружность на 10 равных частей.

На рис. 58, а изображен шкив, а на рис. 58, в — чертеж шкива, где окружность разделена на семь равных частей.

Деление окружности на семь равных частей показано на рис. 58, б. Из точки А проводится вспомогательная дуга радиусом R,равным радиусу данной окружности, которая пересечет окружность в точке п. Из точки п опускают перпендикуляр на горизонтальную осевую линию. Из точки 1 радиусом, равным отрезку nс, делают по окружности семь засечек и получают семь искомых точек.

Деление окружности на любое число равных частей. С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (табл. 10).

Зная, на сколько частей (n) следует разделить окружность, находят по таблице соответствующий коэффициент к. При умножении коэффициента к на диаметр окружности D получают длину хорды l, которую циркулем откладывают на окружности n раз.

При построении чертежа кольца (рис. 59, а) необходимо окружность диаметра D= 142 мм разделить на 32 равные части. Зная число n, по таблице находим коэффициент к = 0,098. Подсчитав длину хорды I = Dk= 142*0,098 — 13,9 мм, циркулем откладывают ее 32 раза (рис. 59, би в).

Значение коэффициента k при делении окружности на n равных частей