Деление окружности на части с помощью транспортира

Во время ремонта часто приходится иметь дело с окружностями, особенно если хочется создать интересные и оригинальные элементы декора. Также часто приходится делить их на равные части. Чтобы сделать это есть несколько методов. Например, можно нарисовать правильный многоугольник или использовать известные всем еще со школы инструменты. Так, для того чтобы разделить окружность на равные части понадобятся сама окружность с четко определенным центром, карандаш, транспортир, а также линейка и циркуль.

Видео:Деление окружности на 12 равных частейСкачать

Деление окружности при помощи транспортира

Разделение окружности на равные части при помощи вышеупомянутого инструмента является, пожалуй, самым простым. Известно, что окружность – это 360 градусов. Разделив это значение на нужное количество частей можно узнать, сколько будет занимать каждая часть (см. фото).

Далее, начиная с любой точки, можно сделать пометки, соответствующие проведенным расчетам. Этот метод хорош, когда окружность нужно разделить на 5, 7, 9 и т.д. частей. Например, если фигуру необходимо разделить на 9 частей, отметки будут находиться на 0, 40, 80, 120, 160, 200, 240, 280 и 320 градусах.

Видео:Деление окружности на 3; 6; 12 равных частейСкачать

Деление на 3 и 6 частей

Чтобы правильно разделить окружность на 6 частей можно использовать свойство правильного шестиугольника, т.е. его самая длинная диагональ должна составлять две длины его стороны. Для начала циркуль необходимо растянуть на длину равную радиусу фигуры. Далее оставляя одну из ножек инструмента в любой точке окружности, второй необходимо сделать засечку, после чего повторяя манипуляции, получится сделать шесть точек, соединив которые можно получить шестиугольник (см. фото).

Соединив вершины фигуры через одну, можно получить правильный треугольник, а соответственно фигуру можно поделить на 3 равные части, а соединив все вершины и проведя через них диагонали можно разделить фигуру на 6 частей.

Видео:1 2 2 деление окружности на 5 равных частейСкачать

Деление на 4 и 8 частей

Если окружность необходимо поделить на 4 равные части, прежде всего, необходимо начертить диаметр фигуры. Это позволит получить сразу две из нужных четырех точек. Далее нужно взять циркуль, растянуть его ножки по диаметру, после чего одну из них оставить на одном из концов диаметра, а другой сделать засечки за пределами круга снизу и сверху (см. фото).

То же необходимо сделать и для другого конца диаметра. После этого полученные за пределами круга точки соединяются при помощи линейки и карандаша. Полученная линия будет вторым диаметром, который будет идти четко перпендикулярно первому, в результате чего фигура будет поделена на 4 части. Для того чтобы получить, например, 8 равных частей, полученные прямые углы можно разделить пополам и провести через них диагонали.

Правильно подобранный анатомический матрас – залог здоровья и комфортного сна. Его основная задача – обеспечить правильную поддержку позвоночника во время.

Сложно представить более простой и абсолютно здоровый способ тепловой обработки еды, чем готовка с помощью электрического гриля. Благодаря уникальному устройству.

Видео:Деление окружности на 3 частиСкачать

Деление окружности на любое число равных частей

Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.

Видео:Деление окружности на 6 равных частейСкачать

Деление окружности на 4 и 8 одинаковых частей

Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

Видео:Измерение угла с помощью транспортираСкачать

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Видео:Деление окружности на равные части с помощью циркуляСкачать

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Видео:Построение угла с помощью транспортираСкачать

Деление окружности

Радиолюбителям, конструкторам, строителям разного рода моделей и вообще любителям мастерить своими руками иной раз приходится задумываться над такой практической

Вырезать из данной пластинки правильный многоугольник с заданным числом сторон.

Эта задача сводится к такой:

разделить окружность на п равных частей, где п — целое число.

Оставим пока в стороне очевидное решение поставленной задачи при помощи транспортира — это всс-таки решение «на глаз» — и подумаем о геометрическом решении: при помощи циркуля и линейки.

Прежде всего возникает вопрос: на сколько равных частей можно теоретически точно разделить окружность при помощи циркуля и линейки? Этот вопрос математиками решен полностью: не на любое число частей.

Можно: на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17. 257. частей.

Нельзя: на 7, 9, 11, 13, 14. частей.

Плохо еще и то, что нет единого способа построения; прием деления, допустим, на 15 частей не такой, как на 12 частей, и т.д., а все способы и не запомнишь.

Практику нужен геометрический способ — пусть приближенный, но достаточно простой и общий для деления окружности на любое число равных дуг.

В учебниках геометрии, к сожалению, еще не уделяют этому вопросу никакого внимания, поэтому приведем здесь один любопытный прием приближенного геометрического решения поставленной задачи.

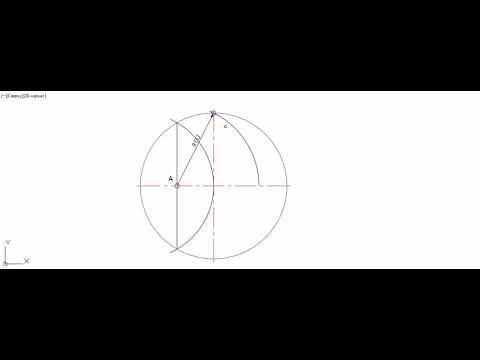
Пусть, например, требуется разделить данную ок

Рис. 148. Приближенный геометрический способ деления окружности на п равных частей

ружность (рис. 148) на девять равных частей. Построим на каком-либо из диаметров АВ окружности равносторонний треугольник ЛСВ и разделим диаметр АВ точкой D в отношении AD : АВ = 2 : 9 (в общем случае AD :АВ = 2:п).

Соединим точки С и D отрезком и продолжим его до пересечения с окружностью в точке Е. Тогда дуга АЕ будет составлять при-

мерно — окружности (в общем случае АЕ =-) или

хорда АЕ будет стороной правильного вписанного девятиугольника (/1-угольника).

Относительная погрешность при этом около 0,8%.

Если выразить зависимость между величиной центрального угла АОЕ, образующегося при указанном построении, и числом делений п, то получится следующая точная формула:

которую для больших значений п можно заменить приближенной формулой

С другой стороны, при точном делении окружности на п равных частей центральный угол должен быть равен 360° 360°

-. Сравнивая угол — с углом АОЕ, получим вели-

чину погрешности, которую мы делаем, считая дугу АЕ 1

— частью окружности. п

Получается такая таблица для некоторых значений п.

📺 Видео

Деление онружности на 5 равных частей циркулем - (Devidin a circle into 5 parts)Скачать

Деление окружности на 5 частей с помощью циркуляСкачать

Построение угла с помощью транспортира. 5 клСкачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Как разделить окружность на 10 частей How to divide a circle into 10 partsСкачать

Как разделить окружность на 5 частей How to divide a circle into 5 partsСкачать

Деление окружности на n- равные частиСкачать

1 2 3 деление окружности на 7 равных частейСкачать

Деление окружности на 3 равные частиСкачать

Деление круга на части без транспортираСкачать

Деление окружности на 4 частиСкачать