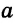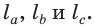Даны прямая а и отрезок ав постройте прямую р параллельную прямой а

Видео:№149. Даны прямая а, точка В, не лежащая на ней, и отрезок PQ. Постройте точку М на прямой a такСкачать

ТЕМА6. Перпендикулярность прямой и плоскости, двух плоскостей или множества геометрических элементов

Задача № 31 Через точку А провести плоскость, параллельную данной.

Задача № 32 Через прямую а провести плоскость, перпендикулярную к плоскости бета, заданной прямыми LK и KM

Задача № 33 На прямой MN найти точку, равноудаленную от точек A и B

Задача № 34 Построить горизонтальную проекцию прямой АВ, пересекающейся с прямой CD при условии, что угол между ними прямой.

Задача № 35 Построить на плоскости треугольника CDE множество точек равноудаленных от концов отрезка AB

Задача № 36 Через точку А провести прямую пересекающую отрезок CD и параллельную плоскости треугольника KLM.

Задача № 37 Через точку А построить прямую параллельную двум плоскостям, заданным следами.

Задача № 38 Провести плоскость параллельную плоскости треугольника АВС, и удаленную от нее на 30 мм.

Видео:Точка, прямая и отрезок. 1 часть. 7 класс.Скачать

Задачи по начертательной геометрии

Ответы на вопросы по заказу заданий по начертательной геометрии:

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?

• Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?

• Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?

• Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! Я стараюсь быть всегда онлайн.

Содержание:

Принятые обозначения

1. Точки, расположенные в пространстве, обозначаются прописными буквами латинского алфавита A,B,C,D,…L,N,…

2. Линии общего положения обозначаются строчными буквами латинского алфавита a,b,c,d,…l,n,…

3. Линии уровня обозначаются: h – горизонталь; f – фронталь.

4. Поверхности обозначаются прописными буквами греческого алфавита

5. Плоскости проекций обозначаются: П₁ — горизонтальная плоскость проекций; П₂ — фронтальная плоскость проекций; П₃ — профильная плоскость проекций. 6. Проекции точек, линий, поверхностей обозначаются теми же буквами, что и оригинал с добавлением индекса плоскости проекций: — горизонтальные проекции; — фронтальные проекции; — профильные проекции.

Символы, обозначающие отношения между геометрическими фигурами: 1. — совпадают: – прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки C и D. 2. – конгруэнтны: — горизонтальная проекция отрезка конгруентна его натуральной длине. 3. — параллельны: – прямая а параллельна прямой b. 4. — перпендикулярны: прямая m перпендикулярна прямой n. 5. — скрещиваются: ,прямые a и b скрещиваются.

Возможно, вас также заинтересует эта ссылка:

Обозначения теоретико-множественных и логических операций:

1. — принадлежит, является элементом: — точка А лежит на прямой m; – прямая n проходит через точку В. 2. — включает, содержит: – прямая а принадлежит плоскости Г; – плоскость проходит через прямую b. 3. — объединение множеств: – ломаная линия АВС есть объединение отрезков 4. — пересечение множеств: – точка К есть результат пересечения прямых а и b. 5. — конъюнкция предложений; соответствует союзу «и». 6. — дизъюнкция предложений; соответствует союзу «или». 7. — импликация – логическое следствие: — если прямые а и b параллельны, то их одноименные проекции также параллельны.

Возможно, вас также заинтересует эта ссылка:

Задачи с решениями

Задача 1.

Определить натуральную длину отрезка АВ(А₁В₁; А₂В₂) и углы его наклона к плоскостям проекций (рис.1, рис.2).

Строим прямоугольный треугольник по двум катетам (см. рис.1). За один катет принимаем фронтальную проекцию А₂В₂ отрезка АВ, за другой катет – отрезок, равный разности расстояний концов отрезка до плоскости П₂. В₀В₂ = А₁А₁ / . Угол β — угол наклона АВ к плоскости проекций П₂. Можно найти длину отрезка АВ, строя прямоугольный треугольник не на фронтальной проекции А₂В₂, а на горизонтальной проекции А₁В₁ (рис.2). Тогда вторым катетом будет разность расстояний концов отрезка до плоскости П₁. В₁В₀ = В₂В₂ / . Угол α — угол наклона отрезка АВ к плоскости проекций П₁.

Задача 2.

На прямой l(l₁, l₂) от точки А(А₁, А₂) отложить отрезок длиной 30 мм (рис.3).

Выделяем на прямой l произвольный отрезок АМ и определяем его натуральную длину. Для этого строим прямоугольный треугольник по двум катетам А₁М₁ и М₁М₀ = М₂М₂ / .

На гипотенузе А₁М₀ построенного треугольника откладываем отрезок А₁С₀ = 30 мм. Опустив из точки С₀ перпендикуляр на горизонтальную проекцию прямой, получаем горизонтальную проекцию А₁С₁ , а по ней и фронтальную А₂С₂ проекции искомого отрезка.

Задача 3.

Через прямую l (l₁, l₂) (рис.11а) провести фронтально проецирующую плоскость ∆ (рис.4).

Признаком принадлежности прямой l фронтально проецирующей плоскости является принадлежность (совпадение) фронтальной проекции l₂ , прямой l с фронтальной проекцией ∆₂ плоскости ∆ , т.е. если (рис.4б).

Задача 4.

Построить проекции линии пересечения двух плоскостей Г(АВС) и (рис.5а).

Плоскость ∆ ( ∆ 2) – фронтально проецирующая. Фронтальная проекция плоскости ∆ обладает собирательным свойством, поэтому фронтальная проекция N₂M₂ искомой линии пересечения совпадает с ∆ ₂. Пользуясь условием, что искомая прямая MN принадлежит и плоскости Г (АВС), находим по фронтальной проекции её горизонтальную проекцию M₁N₁ (рис.5б).

Задача 5.

Построить проекции точки пересечения прямой l (l₁, l₂) с плоскостью Г(АВС). Определить видимость прямой l (l₁, l₂) относительно плоскости Г (рис.6а).

Для решения задачи следует последовательно выполнить следующие три операции (рис.6б). 1-я операция. Через прямую l провести фронтально проецирующую плоскость ∆ (∆ ₂ ) (см. задачу 3). 2-я операция. Построить проекции линии пересечения обеих плоскостей – данной Г и вспомогательной ∆, т.е. MN (M₁N₁; M₂N₂) (см. задачу 4). 3-я операция. В пересечении проекций данной прямой l и построенной MN отметить проекции (К₁, К₂) искомой точки.

Найдя точку пересечения, перейти к определению видимости прямой l . Для определения видимости прямой l на горизонтальной проекции (вид сверху) рассматриваем две горизонтально конкурирующие точки По фронтальной проекции видим, что точка 1 лежит по отношению к плоскости П₁ выше, чем точка 2. Это значит, что сверху видимой является точка 1, а точка 2 закрыта ею. Следовательно, на виде сверху отрезок прямой l , на котором лежит точка 2, является невидимым. На фронтальной проекции видимость можно определить, например, при помощи фронтально конкурирующих точек и

Сравниваем расстояние их по отношению к плоскости П₂ . Сравнение показывает, что точка 3 прямой l , а следовательно, отрезок 3К, спереди не виден.

Задача 6.

В плоскости провести горизонталь и фронталь

Известно, что фронтальная проекция h₂ горизонтали h всегда параллельна оси XO. Поэтому построение горизонтали начинаем с проведения (рис.7б). Горизонтальную проекцию находим из условия принадлежности горизонтали h плоскости Г. Фронтальная проекция горизонтали пересекает фронтальные проекции данных прямых l₂ и m₂ в точках 1₂ и 2₂ , которым соответствуют горизонтальные проекции 1₁ и 2₁. Через них и пройдет горизонтальная проекция h₁ искомой горизонтали h . На (рис.7б) в плоскости Г построена и фронталь f (f₁; f₂). Это построение выполнено аналогично построению горизонтали.

Задача 7.

Даны плоскость и точка D(D₁; D₂). Опустить перпендикуляр из точки на эту плоскость (рис.8). Известно, что если прямая перпендикулярна плоскости, необходимо, чтобы горизонтальная проекция прямой была перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция – фронтальной проекции фронтали плоскости.

Проводим горизонталь h (h₁; h₂ ) и фронталь f ( f₁; f₂) (см. задачу 6). Затем проводим проекции перпендикуляра: горизонтальную n₁ – через D₁ перпендикулярно горизонтальной проекции горизонтали h₁ , и фронтальную n₂ – через D₂ перпендикулярно проекции фронтали f₂ .

Задача 8.

Из произвольной точки плоскости восстановить перпендикуляр (нормаль) к плоскости (рис.9а).

Признаки перпендикулярности прямой и плоскости позволяют строить на чертеже проекции нормали к плоскости. На рис.16б дано построение нормали n ( n₁; n₂) в точке К (К₁ ; К₂) к плоскости Г (l ∩ m). Проекции нормали перпендикулярны соответствующим проекциям линий уровня плоскости Г.

Задача 9.

Даны плоскость и точка D; требуется определить расстояние от точки D до плоскости, заданной двумя пересекающимися прямыми l и m (рис. 10).

Порядок решения задачи: 1. Опустить перпендикуляр из точки D на плоскость (см. задачу 7). 2. Определить точку пересечения перпендикуляра с плоскостью и отделить видимый участок перпендикуляра от невидимого, считая плоскость непрозрачной (см. задачу 5). 3. Определить натуральную величину расстояния от точки D до плоскости Г (см. задачу 1).

Задача 10.

Дана точка К(К₁;К₂) и плоскость Г (АВС) провести через точку К плоскость, параллельную заданной плоскости Г (рис. 11). Построение эпюра параллельных плоскостей основано на известном из стереометрии признаке: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Проводим через точку К(К₁;К₂) прямые l (l1, l2) и m (m₁ ; m₂), параллельно сторонам АВ(А₁В₁,А₂В₂) и АС(АС₁,АС₂).Плоскости параллельны, т.к. их пересекающиеся прямые удовлетворяют условию:

Задача 11.

Построить плоскость параллельную плоскости Г (АВС) и отстоящую от неё на расстоянии 40 мм (рис. 12). План решения задачи: 1. Из произвольной точки С (С₁;С₂) заданной плоскости восстановить перпендикуляр к ней и ограничить его точкой N(N₁;N₂) (см. задачу 8). 2. Определить натуральную величину отрезка перпендикуляра по его проекции C₁N₁ и C₂N₂ (см. задачу 1).

3. На действительной величине отрезка перпендикуляра найти точку М₀ на заданном расстоянии, считая от плоскости, и построить проекции этой точки М(М₁;М₂) на проекциях перпендикуляра (см. задачу 2).

4. Задать искомую плоскость, соблюдая условие параллельности плоскостей (см. задачу 10).

Задача 12.

Через прямую l (l₁,l₂) провести плоскость ∆, перпендикулярную к плоскости (рис.13).

Если плоскость содержит в себе перпендикуляр к другой плоскости, то эти плоскости взаимно перпендикулярны. Чтобы провести через прямую l (l₁, l₂) искомую плоскость, надо из какой-либо точки прямой, например, А(А₁;А₂), провести перпендикуляр к данной плоскости. Строим проекции горизонтали h(h₁;h₂) и фронтали f(f₁;f₂) плоскости Затем, проведя получим проекции перпендикуляра к

плоскости Г. Этот перпендикуляр АВ (А₁В₁; А₂В₂) совместно с данной прямой l (l₁, l₂) определяют искомую плоскость

Задача 13.

Построить линию пересечения двух плоскостей Г(АВС) и ∆(DEF) и отделить видимые их части от невидимых (рис.14).

Первая часть задачи сводится к построению линии пересечения двух плоскостей. Известно, что линией пересечения двух плоскостей является прямая линия, для построения которой достаточно определить две точки, общие обеим плоскостям. В данном случае общие точки для обеих плоскостей найдены как точки пересечения: М – стороны DE треугольника DEF с плоскостью Г(АВС); N – стороны ВС треугольника АВС с плоскостью ∆(DEF). Точка М определена с помощью вспомогательной фронтально проецирующей плоскости θ(θ₂), точка N – посредством горизонтально проецирующей плоскости Σ(Σ₁) проведенных через DE и BC соответственно. Линия пересечения плоскостей ограничена отрезком MN прямой, заключённым между точками встречи контура одной фигуры с ограниченной плоскостью другой.

Найдя линию пересечения, переходим к отделению видимых участков пластинок от невидимых, начав с горизонтальной проекции (вид а сверху). С этой целью рассмотрим две горизонтально конкурирующие точки

Сравнивая расстояния фронтальных проекций этих точек по отношению к плоскости П₁. замечаем, что точка 6 пластинки DEF, а следовательно, и участок стороны DE, находится под плоскостью пластинки АВС. В точке М происходит переход невидимого участка прямой DE к видимому. Аналогичными рассуждениями при помощи фронтально конкурирующих точек определяем видимость на фронтальной проекции.

Задача 14.

Дана точка А(А₁;А₂). Найти её проекции в системе П₁/П₄ (рис.15а). На рис. 15 показаны те построения, которые надо произвести на эпюре, чтобы от проекций точки А(А₁;А₂) в системе П₁/П₂ перейти к проекциям (А₁;А₄) той же точки в системе П₁/П₄.. 1.Опускаем из А₁ перпендикуляр на новую ось проекций П₁/П₄. На построенном перпендикуляре откладываем (от новой оси) отрезок А₄А_х ‘ =А₂А_х. Полученная таким образом точка А₄ является проекцией точки А(А₁;А₂) на новую плоскость проекции П₄.

Задача 15.

Дана точка А(А₁;А₂) найти её проекции в системе П₂/П₄ (рис.15б). На рис.15б показаны те построения, которые надо произвести на эпюре, чтобы от проекции (А₁;А₂) точки А в системе П₁/П₂ перейти к проекциям (А₂; А₄) той же точки в системе П₂/П ₄ .

Для построения на эпюре новой проекции точки при замене одной из плоскостей проекций надо опустить перпендикуляр на новую ось из той же проекции точки, которая не меняется, и отложить на нем от новой оси в соответствующую сторону расстояние от заменяемой проекции до старой оси.

Задача 16.

Преобразовать горизонтально проецирующую плоскость Г(АВСD) в плоскость уровня (рис.16).

Плоскость Г – горизонтально проецирующая. Для преобразования ее в плоскость уровня достаточно взамен плоскости проекции П₂ ввести новую плоскость П₄ , параллельную плоскости Г(АВСD). Линию пересечения плоскостей П₁ и П₄ принимаем за новую ось проекций X₁.

Новая ось X₁ параллельна вырожденной проекции Г₁ плоскости Г, т.к. плоскость П₄ параллельна данной плоскости Г. Построив проекции точек А, В, С и D в новой системе П₁ П₄ и соединив их, получим проекцию четырехугольника А₄В₄С₄D₄, отображающего свои натуральные размеры.

Задача 17.

По данной фронтальной проекции К₂ точки К построить горизонтальную проекцию К₁, исходя из условия, что точка К принадлежит грани SАС (рис.17). Построение точки на поверхности выполняется как построение точки на плоскости грани.

На грани SАС при помощи прямой 1–2 (1₁2₁ ; 1₂2₂) по данной фронтальной проекции К₂ точки К построена горизонтальная проекция К₁ , исходя из условия, что точка К должна лежать в грани SАС. На рис.18 показано построение К₁ на грани SВС при помощи прямой, проведенной через вершину S пирамиды.

Задача 18.

Задать на поверхности конуса произвольную точку А (рис.19).

1-й способ (рис.19а). На основании конуса задаем произвольную точку К(К₁ , К₂) и проводим вспомогательную образующую через точки S и К. На этой образующей берем точку А, которая и лежит на заданной поверхности. 2-й способ (рис.19б). На поверхности конуса проводим вспомогательную параллель; ее фронтальная проекция является отрезком прямой, параллельным оси проекций XO, а горизонтальная проекция – окружностью. На этой параллели берем точку А , которая и лежит на поверхности.

Задача 19.

Построить горизонтальную проекцию линии на поверхности конуса по заданной фронтальной проекции (рис.20).

Построение горизонтальной проекции заданной линии начинаем с того, что отмечаем точки, принадлежащие очерковым образующим. Эти точки называют характерными. Точка 3 принадлежит передней образующей, 8 – задней, 2 – правой, 1 – левой и точка 10 – основанию конуса. Между этими точками отмечают так называемые случайные точки, помогающие установить характер линии. Точки 4, 5, 6, 7 и 9 – случайные. Горизонтальные проекции всех отмеченных точек находим из условия принадлежности их конусу (см. задачу 16). При соединении точек следует учитывать их видимость. В нашем примере все точки сверху видимы, поэтому и линия, соединяющая их, видима сверху.

Задача 20.

Построить проекции линии пересечения пирамиды SАВСD с проецирующей плоскостью Г(Г₂) (рис.21).

Известно, что любая поверхность пересекается плоскостью по некоторой линии, точки которой принадлежат как поверхности, так и пересекающей плоскости. Общим приемом построения проекций линии пересечения поверхности плоскостью является построение отдельных точек, принадлежащих этой линии, с последующим соединением их в определенной последовательности. Линия пересечения поверхности любого многогранника плоскостью будет ломаная линия, которая состоит из отрезков прямых, являющихся линиями пересечения отдельных граней рассматриваемого многогранника с указанной плоскостью. Характерными точками этой линии будут ее вершины, расположенные на ребрах многогранника. В нашем примере пирамида пересекается фронтально проецирующей плоскостью это значит, что фронтальная проекция искомой линии пересечения непосредственно задана на чертеже и совпадает с фронтальной проекцией всей плоскости Г₂ . При помощи линии связи находим горизонтальные проекции сечения. Натуральная величина сечения определена способом замены плоскостей проекций (см. задачу 14). За новую горизонтальную плоскость проекций взята сама плоскость Г. Новой осью проекций является Г₂ .

Возможно, вас также заинтересует эта ссылка:

Задача 21.

Построить в прямоугольной изометрии сечение пирамиды фронтально проецирующей плоскостью. Пирамида задана своими ортогональными проекциями (рис.22).

Через точку О₁ проводим прямые x , y, z , которые принимаем за оси натуральной системы координат (рис.29а). Вычерчиваем аксонометрические оси координат с углами в 120 0 между ними (рис.22б). По координатам, определенным непосредственным измерением ортогонального чертежа, строим аксонометрическую и вторичную горизонтальную проекции пирамиды. В нашем примере основание пирамиды АВСDЕ лежит на плоскости XOY, поэтому ее вторичная проекция совпадает с аксонометрической проекцией и обозначена Далее по координатам X и Y вершин сечения строим вторичную горизонтальную проекцию сечения Затем из точек проводим проецирующие прямые, параллельные оси до пересечения с соответствующими ребрами пирамиды в точках Соединяя найденные точки, получим фигуру сечения пирамиды фронтальнопроецирующей плоскостью. Для решения задачи на построение линии пересечения двух фигур, одна из которых занимает проецирующее положение, достаточно выделить на чертеже уже имеющуюся проекцию линии пересечения, которая совпадает с вырожденной проекцией проецирующей фигуры. Вторую проекцию линии пересечения надо построить, исходя из условия ее принадлежности фигуре, занимающей общее положение.

Для решения этой задачи необходимо знать решение задач 18, 19, 20, а также нижеследующие задачи.

Возможно, вас также заинтересует эта ссылка:

Задача 22.

Построить горизонтальную проекцию плоской линии, принадлежащей поверхности конуса (рис.23). Определяем плоскую кривую. Так как плоскость, в которой находится кривая, параллельна образующей конуса, то кривая – парабола . Строим характерные точки А , М , N , — они находятся на известных линиях поверхности. Случайные точки 1 , 2, 3 , 4 строим с помощью параллелей конуса (см. задачу 18).

Задача 23.

Построить фронтальную проекцию плоской линии, принадлежащей поверхности конуса (рис.24). Кривая – гипербола, т.к. расположена в плоскости, параллельной двум образующим конуса.

Строим характерные точки: А (вершина гиперболы); N , M – конечные точки гиперболы; Т – точка видимости фронтальной проекции линии. Случайные точки строим с помощью параллелей конуса.

Задача 24.

Построить фронтальную проекцию плоской линии, принадлежащей поверхности сферы (рис.25). Кривая – окружность , которая проецируется на фронтальную плоскость проекций в эллипс, т.к. плоскость окружности наклонена к П₂ . Характерные точки кривой — А , В и С , D (определяющие большую и малую оси эллипса), а также К и Т — точки видимости. Случайные точки — 1 , 2. Фронтальную проекцию точек строим с помощью окружностей, параллельных фронтальной плоскости.

Задача 25.

Построить горизонтальную проекцию линии, принадлежащей поверхности пирамиды (рис.26). Характерные точки К , Т , N , D , принадлежащие ребрам пирамиды, и М , R – крайняя левая и самая низкая.

Горизонтальные проекции точек определяем с помощью прямых, параллельных основанию пирамиды.

Возможно, вас также заинтересует эта ссылка:

Задача 26.

Построить пересечение конуса и призмы (рис.27). Призма занимает проецирующее положение по отношению к фронтальной плоскости проекций, поэтому фронтальная проекция искомой линии пересечения совпадает с вырожденной проекцией призмы в пределах очерка конуса. Линия пересечения будет состоять из части эллипса и части окружности радиуса R . Характерными точками будут А , С , D и M , N для эллипса и M , N , K для окружности; CD – малая ось эллипса; M , N – точки излома; K – крайняя правая точка окружности, определяющая радиус окружности R . Случайные точки – 1 , 2, 3 , 4 . Горизонтальные проекции точек определяем с помощью параллелей конуса. Определяем видимость кривой, учитывая, что проекция линии пересечения видима, если она принадлежит видимой части одной и второй поверхности.

Задача 27.

Построить развертку пирамиды SABC (рис.28). Гранями пирамиды являются треугольники, для построения которых достаточно определить натуральные длины их сторон – ребер пирамиды.

Основание пирамиды параллельно плоскости П₁,поэтому подлежат определению только натуральные величины боковых ребер пирамиды. Строим развертку боковой поверхности пирамиды, используя натуральные величины ребер. Для этого по трем сторонам строим контур одной грани, к ней пристраиваем следующую и т.д.

Задача 28.

Построить на развертке цилиндра линию, принадлежащую поверхности цилиндра (рис.29).

• Строим развертку цилиндра – прямоугольник, у которого одна сторона – высота цилиндра, другая – длина окружности основания. Выделяем образующие на поверхности цилиндра и наносим их на развертку. Строим точки, лежащие на образующих и принадлежащие кривой.

Задача 29.

Построить точки пересечения прямой с поверхностью (рис. 30): а) поверхность коническая; б) поверхность сферическая.

• Через прямую проводим секущую плоскость так, чтобы она пересекла конус или сферу по окружности. Точки пересечения прямой и линии сечения К и Т являются точками пересечения прямой с поверхностью.

Задача 30.

Построить пересечение двух поверхностей (рис.31). Для решения задачи такого типа применяется метод секущих плоскостей. Секущие плоскости – посредники выбираются так, чтобы при пересечении с каждой из поверхностей образовывались удобные для построения линии (прямые или окружности). В данном примере в качестве посредников выбираем горизонтальные плоскости, которые рассекают тор и сферу по окружностям. Строим характерные точки А, В, К, Т. Для определения К и Т используем плоскость – посредник Г.

Случайные точки определяем с помощью плоскостей Определяем видимость кривой пересечения, учитывая, что на горизонтальной проекции видима только верхняя половина сферы.

Возможно, вас также заинтересует эта ссылка:

Задача 31.

Построить пересечение соосных поверхностей вращения цилиндра и сферы, конуса и сферы (рис. 32).

Соосные поверхности пересекаются по общим параллелям (окружностям), плоскости которых, как известно, перпендикулярны осям вращения. Определяем характерные точки А, В как точки пересечения очерков. Строим линии пересечения поверхностей.

Задача 32.

Построить пересечение двух поверхностей вращения, оси которых пересекаются в точке О (рис.33). Используем секущие сферы, центры которых находятся в точке О.

• Каждая сфера-посредник соосна с обоими пересекающимися цилиндрами. Линии пересечения сферы и цилиндра пересекаются между собой и определяют точки, принадлежащие линии пересечения двух цилиндров. Для определения радиусов максимальной и минимальной секущих сфер решаем следующие задачи.

R_max есть величина, равная расстоянию от О₂ до самой далекой характерной точки А₂. Для определения R_min вписываем сферы в каждую из пересекающихся поверхностей R₁ и R₂ . Минимальным радиусом секущей сферы ( R_min ) будет больший из двух радиусов вписанных сфер — R₂ = R_min .

Задача 33.

Через прямую АВ (А₆ , В₆ ) (рис.34а) провести плоскость Σ , уклон которой Строим сетку углового масштаба и с его помощью определяем интервал плоскости l (рис. 34 б). Сторона каждого квадрата сетки углового масштаба соответствует 1 м.

• Так как прямая АВ является горизонтальной прямой, то она является одной из горизонталей искомой плоскости.
• Проводим перпендикулярно горизонтали искомой плоскости направление масштаба уклонов на котором от заданной прямой откладываем отрезки, равные интервалу l, определенному с помощью углового масштаба. Через полученные отметки проводим ряд горизонталей плоскости

Задача 34.

Через прямую АВ (А₅ , В₆) провести плоскость уклон которой масштаб 1 : 200 (рис.35).

• Строим сетку углового масштаба и определяем интервал плоскости (в масштабе 1:200 сторона каждого квадрата сетки – 0,5 см).
• Вычерчиваем вспомогательный конус, вершина которого расположена на заданной прямой в точке, имеющей целую отметку (например В₆), а уклон образующей равен уклону искомой плоскости. Плоскость эта должна проходить через заданную прямую АВ и касаться конуса.

Радиус R основания конуса равен интервалу плоскости L , высота конуса равна 1м. Из точки В₆ чертежа радиусом R = L проводим окружность – горизонталь поверхности конуса, имеющую отметку 5. Касательная АК (А₅ , К₅) является горизонталью искомой плоскости. Направление масштаба уклона плоскости перпендикулярно горизонтали АК.

Задача 35.

Через заданную на чертеже дугу BCD окружности, лежащую в горизонтальной плоскости, провести коническую поверхность (рис.36). Уклон образующих i = 3 : 4, масштаб 1 : 200. Из центра дуги проводим нормаль, и от места её пересечения с дугой (внутрь или наружу) откладываем отрезки, равные интервалу конической поверхности. На рис. 36 а представлен фрагмент насыпи, а на рис. 36 б – фрагмент выемки.

Задача 36.

Построить линию пересечения двух плоскостей откоса дна котлована с бровками АВ и ВС. Уклон откосов i = 2:3, масштаб 1 : 200 (рис.37а).

• Заданные прямые АВ и ВС являются горизонталями плоскостей откоса. Проводим масштаб уклона перпендикулярно АВ с интервалом L , определённым из углового масштаба, Аналогично строим масштаб уклонов (рис.37б).
• Строим горизонтали плоскостей откосов, Через точки пересечения горизонталей с одинаковыми отметками проводим линию пересечения плоскостей откосов BD.

Строим горизонтали плоскости Ʃ и дуги окружностей – горизонталей конической поверхности. Находим точки пересечения одноименных горизонталей и соединяем их плавной кривой, которая является искомой линией пересечения

Задача 38.

Определить линию пересечения топографической поверхности с плоскостью заданной масштабом уклонов (рис. 39).

Решение сводится к определению точек пересечения горизонталей плоскости и топографической поверхности, имеющих одинаковые отметки, которые соединяются между собой отрезками ломанной линии.

Задача 39.

Определить линию пересечения конической и топографической поверхности (рис. 40). Аналогично предыдущей задаче находим точки пересечения одноименных горизонталей и соединяем их отрезками ломаной линии. Для уточнения контура, поскольку тридцать пятые горизонтали не пересекаются, дополнительно проводим (штриховой линией) горизонтали с отметкой 34,5, проведенные интерполяцией.

Задача 40.

Построить профиль 1-1 топографической поверхности (рис. 41а). Точки пересечения горизонталей поверхности с вертикально проецирующей плоскостью при помощи полоски бумаги с рис. 41а переносим на рис. 41б на горизонтальную линию. Из полученных точек восставляются перпендикуляры до пересечения с горизонтальными линиями, имеющими такие же отметки, как и отмеченные точки. Линия, соединяющая полученные точки пересечения, представляет собой профиль топографической поверхности.

Задача 41.

Определить границы земляных работ на прямолинейном горизонтальном участке дороги с отметкой 20. Уклоны откосов выемок 1:1, уклон откосов насыпей 1:1,5 (рис.42).

Так как дорога имеет отметку 20, то точки нулевых работ находятся в пересечении горизонталей с отметкой 20 с бровками дороги — точки 0. В этих точках соприкасаются границы земляных работ выемки и насыпи.

Анализируя положение горизонталей на плане местности с отметкой полотна дороги, можно заметить, что левые точки нулевых работ часть дороги будет находится в выемке, так как в этом направлении рельеф местности повышается (горизонтали топографической поверхности имеют большие отметки, чем полотно дороги), а справа – на насыпи (рельеф местности на этом участке понижается). С помощью углового масштаба уклонов определяем интервалы откосов выемки и откосов насыпей. Перпендикулярно бровкам дороги проводим масштабы уклонов плоскостей откосов выемки и масштабы уклонов плоскостей откосов насыпи

Проведя горизонтали плоскостей откосов, определяем точки пересечения этих горизонталей с одноименными горизонталями топографической поверхности. Линии, соединяющие полученные точки, являются границами земляных работ.

Задача 42.

Определить линию пересечения откоса насыпи с топографической поверхностью в случае, когда их горизонтали не пересекаются (рис.43)

В рассматриваемом примере горизонтали с отметками 8 и 10 плоскости откоса насыпи не пересекаются с горизонталями 9 и 10 топографической поверхности. Для определения точки, принадлежащей линии пересечения, проводим в плоскости откоса произвольную прямую А₁₀В₉ и определяем точку ее пересечения с топографической поверхностью, проводя для этого через прямую вспомогательную плоскость ( эта плоскость определяется параллельными прямыми AD и BC). Линия пересечения D₁₀C₉ вспомогательной плоскости с топографической поверхностью определяет в пересечении с прямой А₁₀В₉ искомую точку К. Вторая общая точка для плоскости откоса к топографической поверхности – точка L определена аналогично.

Задача 43.

По ортогональным проекциям построить прямоугольную изометрию (рис.44а).

Построение изометрии необходимо проводить в такой последовательности: а) на ортогональном чертеже задать проекции осей натуральной системы координат (рис.44б);

б) задать аксонометрические оси и построить вторичную проекцию (аксонометрию плана) (рис.44в); в) построить аксонометрию всей фигуры (рис.44г).

Задача 44.

Построить собственные и падающую тень призмы на горизонтальную плоскость (рис.45). Прежде, чем строить падающую тень призмы, определяем контуры собственной тени, рассматривая положение граней относительно направления лучей света. В тени находятся правая, задняя и нижняя грани призмы. Контур собственной тени призмы при заданном направлении световых лучей представляет собой ломаную линию АВСDЕ, составленную из ребер призмы.

От контура собственной тени строим контур падающей тени. Так как ребро АВ перпендикулярно горизонтальной плоскости, то направление тени от отрезка АВ на горизонтальной плоскости параллельно вторичной проекции светового луча

(проекции луча на этой плоскости). Отрезки ВС и DC параллельны горизонтальной плоскости, поэтому тени этих отрезков на эту плоскость параллельны самим отрезкам.

Задача 45.

Построить тень, падающую от отрезка АВ на призму (рис. 46).

Тень от вертикального отрезка на землю (горизонтальную плоскость) совпадает с направлением вторичной проекции светового луча. Но она действительна до точки так как эта точка лежит на линии пересечения плоскости земли с гранью призмы. В этой точке тень от отрезка преломляется на грань призмы. Тень от отрезка АВ , упавшая на вертикальную грань призмы, изобразится вертикальной прямой так как АВ параллелен этой грани. Тень от отрезка АВ, упавшая на верхнюю грань призмы, совпадает с направлением вторичной проекции светового луча, т.е.

Задача 46.

Построить собственные и падающие тени заданных призм (рис. 47). Определяем грани, находящиеся в собственной тени, и контуры этих теней. Это – правые, задние и нижние грани призм.

Построение падающих теней от ребер на горизонтальную плоскость выполнено аналогично с построениями в примере 46 (см. рис.47). Построение падающей тени вертикального отрезка EF аналогично построениям, выполненным при решении задачи 46. Тень от ребра FK падает на вертикальную (переднюю грань) и горизонтальную (верхняя грань) плоскости. Тень от отрезка FK по вертикальной плоскости будет направлена от точки в точку 1 / (точку пересечения ребра FK с этой вертикальной плоскостью) на участке Тень от отрезка FK на горизонтальной плоскости будет параллельна самому отрезку Тень от отрезка МК падает на горизонтальную плоскость, и поэтому параллельна самому отрезку.

Задача 47.

По ортогональному чертежу прямой l построить перспективу (рис.48а).

Выполним предварительные построения на ортогональном чертеже. Задаем основание главного луча S₁P₁ ,проведя (рис.48б). Определяем картинный след прямой (точку пересечения прямой с картиной) — Для построения точки схода F прямой l проводим через S₁ прямую и отмечаем точку являющуюся основанием точки схода. Выполним предварительные построения на картине (рис.48в). Зададим линии hh и OO , расстояние между которыми равно высоте точки зрения, т.е. расстоянию от S₂ до оси X на ортогональном чертеже. На hh , примерно посередине, проведем главную линию картины

Затем приступаем к построению перспективы прямой. Так как прямая l – горизонтальная прямая, то точка схода прямой (и ее вторичная проекция) лежит на hh , а картинный след (и его вторичная проекция) – на OO. Построим эти точки, отложив Соединив построенные точки, получаем перспективу прямой 1 . Так прямая 1 принадлежит предметной плоскости, то перспектива прямой и ее вторичная проекция совпадают.

Задача 48.

Построить перспективу отрезка АВ (рис.49). Перспектива точки строится в пересечении перспектив двух прямых, проходящих через точку в пространстве. Строим перспективу прямой l , которой принадлежит отрезок АВ (см. предыдущую задачу). Чтобы на построенной прямой зафиксировать положение определенной точки, в пространстве через эту точку проводим вспомогательную прямую и строим перспективу этой прямой. Вспомогательные прямые могут быть любого направления. Для построения перспективы точки В через нее проводим прямую n , перпендикулярную картине В перспективе известна точка схода такой прямой – она совпадает с главной точкой картины. Для построения перспективы точки А через нее проведена прямая m, проходящая через точку стояния (основание точки зрения). Для этой прямой известно направление ее в перспективе – она параллельна главной линии.

Задача 49.

Построить перспективу плана здания (рис.50).

При анализе формы плоской фигуры замечаем, что она содержит отрезки из пучков параллельных прямых. Построив точку схода перспективных изображений пучка прямых АВ, ЕМ, КN и их картинные следы строим перспективу этих прямых. Заметим, что пучок параллельных прямых АЕ, ВС, КТ, MN не имеет в пределах чертежа доступную точку схода. Поэтому на перспективном изображении положение каждой вершины многоугольника плана определен с помощью вспомогательных прямых, проходящих через точку стояния (см. в задаче 48 построение перспективы точки В).

Возможно, вас также заинтересует эта ссылка:

Задача 50.

Построить перспективу вертикального отрезка АВ (рис.51).

Вначале строим перспективу точки А, принадлежащей предметной плоскости. Для этого проводим через точку А две вспомогательные прямые: t – идущую в точку стояния.

Через перспективу точки А проводим вертикальную прямую – направление перспективы отрезка АВ. Для того чтобы получить перспективу точки В , через прямую n проводим вертикальную плоскость и строим линию пересечения плоскости с картиной затем, отложив на этой прямой от основания картины отрезок равный величине отрезка проводим в плоскости горизонталь заданной высоты до пересечения с вертикальной прямой – направлением перспективы отрезка АВ. Заметим, что прямая n является нулевой горизонталью плоскости (предметным следом плоскости ). Так как горизонталь параллельна n , то в перспективе они пересекаются в общей точке схода (в нашем примере точкой схода является главная точка картины, так как

Задача 51.

Построить собственные и падающую тень призмы при заданном направлении светового луча (рис. 52). Прежде чем строить падающую тень призмы, определяем контур собственной тени. Так как при заданном направлении световых лучей в тени находятся правая и задняя часть призмы, то контур собственной тени представляет собой ломаную линию ABCDE, составленную из ребер призмы. Строим контур падающей тени от контура собственной тени. Так как ребро АВ перпендикулярно предметной плоскости, то направление тени от отрезка АВ

совпадает с направлением вторичной проекции светового луча. В пересечении перспективы светового луча и вторичной проекции его отмечаем тень от точки, через которую проходит световой луч. Заметим, что в данной задаче направление световых лучей параллельно плоскости картины (вторичная проекция заданного светового луча параллельна линии hh), и поэтому на перспективном изображении сохраняется параллельность световых лучей.

Задача 52.

Построить тень, падающую от отрезка АВ (рис.53).

Тень от отрезка АВ на предметной плоскости направлена по вторичной проекции светового луча. Она действительна до точки в которой тень от отрезка преломляется на грань призмы

Отрезок АВ параллелен вертикальной грани призмы, поэтому тень от него на этой грани будет вертикальна (участок Тень от отрезка АВ, упавшая на верхнею грань призмы, совпадает с направлением вторичной проекции светового луча

Задача 53.

Построить собственные и падающие тени заданных призм (рис. 54).

Определяем грани находящиеся в собственной тени, и контуры этих теней. В тени находятся правые и задние грани призм. Построение падающих теней от ребер призмы на предметную плоскость выполнено аналогично с построением в задаче 51 (см. рис. 52). Построение падающей тени вертикального отрезка АВ выполнено аналогично с построениями в задаче 52 (см. рис. 53). Тень от отрезка ВС падает на вертикальную (передняя грань) и горизонтальную (верхняя грань) плоскости. Для построения тени от отрезка ВС на передней грани определяем точку пересечения этого отрезка с плоскостью – точку Тень отрезка АВ по вертикальной плоскости направлена от точки до точки на участке Тень от отрезка ВС на горизонтальной плоскости (верхней грани) параллельна самому отрезку BC, и поэтому перспектива отрезка и тень от него на этой плоскости пересекаются в общей точке схода.

Отрезок CD также параллелен горизонтальной плоскости, на которую падает тень от него, поэтому тень и перспектива этого отрезка пересекаются в общей точке схода.

Возможно, вас также заинтересует эта ссылка:

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Видео:№36. Прямая с пересекает прямую а и не пересекает прямую b, параллельную прямой а.Скачать

Задачи на построение по геометрии с примерами решения

Содержание:

Ранее мы выполняли построения на плоскости при помощи линейки с делениями, чертежного треугольника, транспортира и циркуля.

Математиков всегда интересовали построения геометрических фигур, которые можно выполнить только при помощи циркуля и линейки. В геометрии специально выделяют задачи на построение, которые могут быть решены с помощью этих двух инструментов.

Например, при помощи циркуля и линейки можно построить треугольник, стороны которого равны трем данным отрезкам. Или построить угол, равный данному углу.

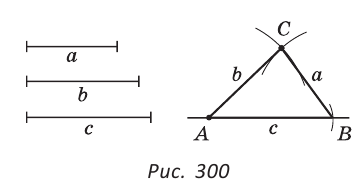
Рассмотрим одну из таких задач на построение. На прямой

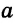
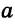
Найти точку — это значит построить ее при помощи циркуля и линейки. Если перемещать некоторую точку по прямой (положения К₁ К₂, К₃), то расстояния от этой точки до точек А и В будут меняться. Когда эти расстояния станут равными, точка на прямой будет равноудалена от концов отрезка АВ. Значит, она будет лежать на серединном перпендикуляре к отрезку АВ. Это и есть идея построения: нужно построить серединный перпендикуляр к отрезку АВ и найти точку его пересечения с прямой .

Чтобы построить серединный перпендикуляр, нужно построить две пересекающиеся окружности равных радиусов с центрами в точках А к В (рис. 293, б). Затем провести прямую MN через точки пересечения этих окружностей (ниже мы обоснуем это построение). В пересечении серединного перпендикуляра MN к отрезку АВ и прямой 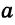получим искомую точку К.

Рассмотренная задача может иметь и практический смысл. Допустим, есть два населенных пункта и шоссе рядом с ними. На шоссе нужно найти место для остановки, чтобы путь для жителей обоих населенных пунктов до остановки был одинаковым. Все построения будут сделаны на карте населенного пункта.

При решении задач на построение линейка считается односторонней и без делений. При помощи такой линейки нельзя построить две параллельные прямые, проведя линии по краям линейки, нельзя измерять и откладывать отрезки, нельзя строить перпендикуляры, используя прямоугольную форму линейки. Рассмотрим, какие операции можно выполнять линейкой, а какие циркулем.

Видео:7 класс. Построение. Часть 09. Задача 284Скачать

Операции с линейкой

При помощи линейки можно провести (построить):

а) произвольную прямую;

б) прямую, проходящую через две точки (рис. 294).

Видео:№ 284 - Геометрия 7-9 класс АтанасянСкачать

Операции с циркулем

При помощи циркуля можно:

а) построить произвольную окружность и окружность (дугу окружности) с данным центром и радиусом, равным данному отрезку (рис. 295);

б) отложить отрезок, равный данному отрезку, на некоторой прямой.

Видео:Отрезок, луч, прямаяСкачать

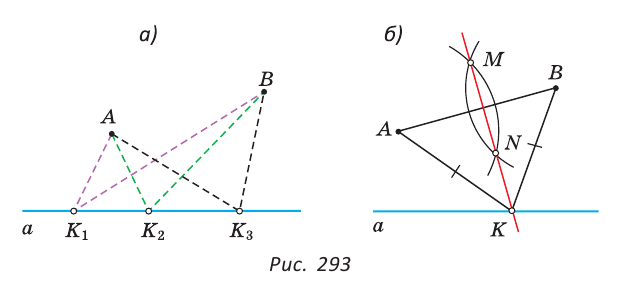
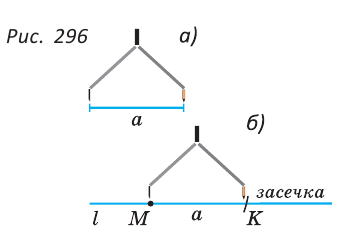
Откладывание отрезка

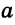
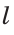
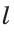
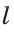
Для откладывания отрезка, равного данному отрезку (рис. 296, а) на прямой (рис. 296, б), следует: 1) отметить на прямой точку М; 2) радиусом, равным а, провести дугу окружности с центром в точке М (сделать засечку на прямой ).

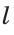
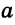
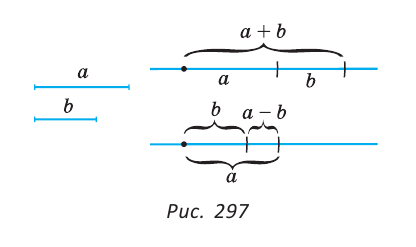
В пересечении дуги и прямой получим точку К и отрезок МК, равный .

Операция откладывания отрезка на прямой позволяет построить сумму и разность двух отрезков (рис. 297): в первом случае на произвольной прямой откладывают последовательно два отрезка, во втором — на большем отрезке от любого его конца откладывают меньший отрезок.

В дальнейшем при решении задач на построение мы не будем описывать процедуру откладывания отрезка на прямой, считая ее элементарной операцией.

Перечислим 5 основных задач на построение, к которым сводятся другие задачи. Решая сложные задачи, будем ссылаться на эти основные, не описывая ту часть решения, которая связана с одной из основных задач.

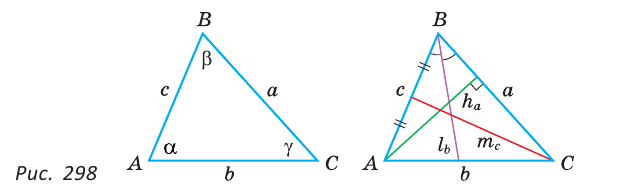
• Задача I. Построение треугольника по трем сторонам.
• Задача II. Построение угла, равного данному.
• Задача III. Построение биссектрисы угла.
• Задача IV. Построение середины отрезка.
• Задача V. Построение прямой, перпендикулярной данной.

В некотором смысле «линейка» и «циркуль» — это два идеальных робота, которые могут выполнять определенный набор операций. И наша задача — составить алгоритм из последовательности таких операций — команд для этих роботов, который приведет к построению необходимой фигуры. Фактически нужно написать программу для «циркуля» и «линейки».

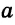
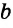
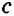
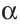
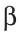
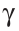
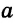
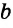
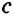
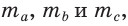
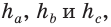
Замечание. В треугольнике ABC стороны, противолежащие углам А, В и С, будем соответственно обозначать , и , а сами эти углы — , и (рис. 298). Медианы, проведенные к сторонам , и , — высоты — биссектрисы —

Видео:№148. На прямой даны две точки А и В. На продолжении луча ВА отложите отрезок ВС так, чтобы ВС= 2АВ.Скачать

Построение треугольника по трем сторонам. Построение угла, равного данному

Задача №1

Построить треугольник со сторонами , и .

Решение:

Пусть даны отрезки , и . На произвольной прямой откладываем отрезок АВ = (рис.300).

Строим окружность с центром в точке А радиусом . Строим окружность с центром в точке В радиусом . Находим точку С пересечения этих окружностей. Проведем отрезки АС и ВС.

Треугольник ABC — искомый, так как у него ВС = , АС = , АВ = по построению.

Задача имеет решение, если для данных отрезков , и выполняется неравенство треугольника:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

💥 Видео

№687. Даны прямая а и две точки А и В, лежащие по одну сторону от этой прямой. На прямой а постройтеСкачать

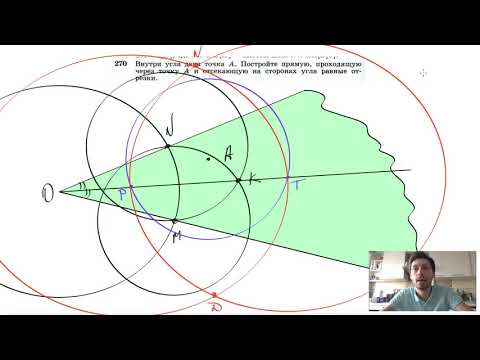
№270. Внутри угла дана точка А. Постройте прямую, проходящую через точку А и отсекающуюСкачать

Построение прямой, параллельной даннойСкачать

№11. Даны прямая и точка, не лежащая на этой прямой. Докажите, что все прямые, проходящие черезСкачать

№199. Прямая р параллельна стороне АВ треугольника ABC. Докажите, что прямые ВССкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Следы прямойСкачать

№204 Концы отрезка АВ лежат на параллельных прямых а и b. Прямая, проходящая через середину ОСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Перпендикуляр к прямой через заданную точку.Скачать