Что такое е на числ окружности

Число e (или, как его еще называют, число Эйлера) – это основание натурального логарифма; математическая константа, являющаяся иррациональным числом.

Способы определения числа e (формула):

1. Через предел:

Второй замечательный предел:

Альтернативный вариант (следует из формулы Муавра – Стирлинга):

2. Как сумма ряда:

Свойства числа e

1. Предел обратного числа e

2. Производные

Производной экспоненциальной функции является экспоненциальная функция:

Производной натуральной логарифмической функции является обратная функция:

3. Интегралы

Неопределенным интегралом экспоненциальной функции e x является экспоненциальная функция e x .

Неопределенный интеграл натуральной логарифмической функции log_e x:

Определенный интеграл от 1 до e обратной функции 1/x равен 1:

Логарифмы с основанием e

Натуральный логарифм числа x определяется как базовый логарифм x с основанием e:

Экспоненциальная функция

Это показательная функция, которая определяется следующим образом:

Формула Эйлера

Комплексное число e iθ равняется:

где i – мнимая единица (квадратный корень из -1), а θ – любое действительное число.

Видео:10 класс, 11 урок, Числовая окружностьСкачать

Что такое экспонента в математике для чайников

Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).

е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).

Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.

Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.

Показательная функция — это математическая функция вида y = a×.

График экспоненты выглядит следующим образом:

Видео:Число e - 2,718. Объяснение математического смысла.Скачать

Для чего используется экспонента?

Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.

Видео:Как искать точки на тригонометрической окружности.Скачать

Экспоненциальный рост

Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.

Видео:Соответствие чисел точкам числовой окружностиСкачать

Что такое второй замечательный предел

Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.

Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.

Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):

То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.

Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:

(1 + 1/1000000) ^ 1000000 = 2.7182804691

Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.

Видео:Точки на числовой окружностиСкачать

Как определить число е?

Помимо второго замечательного предела, существуют и другие способы для определения числа е:

• через сумму ряда;
• через формулу Муавра — Стирлинга;
• другие.

Сумма ряда

Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.

Можно получить приближение е, рассчитав первые 7 частей этой суммы:

И эти вычисления дали нам следующий результат:

Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.

Формула Муавра — Стирлинга

Также называется просто формула Стирлинга:

И в этом случае чем больше n, тем точнее будет результат.

Видео:Поясняю за число ПиСкачать

Как запомнить число е

Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.

Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.

Видео:ТРИГОНОМЕТРИЯ С НУЛЯ - Единичная Окружность // Подготовка к ЕГЭ по МатематикеСкачать

Интересные факты

Экспоненциальную функцию также называют экспонента.

Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.

А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):

Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как .

Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).

Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.

Видео:Число Пи-здесь. Объяснение математического смысла.Скачать

Число Непера и число Эйлера

Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.

Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.

Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.

Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.

Узнайте также, что такое Число Пи и Логарифм.

Константу впервые вычислил швейцарский математик Якоб Бернулли в ходе решения задачи о предельной величине процентного дохода. Он обнаружил, что если исходная сумма $1 и начисляется 100% годовых один раз в конце года, то итоговая сумма будет $2. Но если те же самые проценты начислять два раза в год, то $1 умножается на 1,5 дважды, получая $2,25 (т. е. 1$*50%=1,5$, затем 1,5$*50%=2,25$). Начисления процентов раз в квартал (4 раза в год, т. е. каждый квартал к новой полученной сумме прибавляем 25%) получаем $2,44140625, и так далее. Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента будет равен числу 2,718.

Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?

Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:

Математическая константа е является основанием натурального логарифма.

Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:

Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.

Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).

С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!

Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

Число е – это не просто число

Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.

Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).

Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.

Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.

Видео:Математика это не ИсламСкачать

Понятие экспоненциального роста

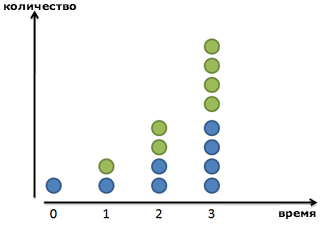
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:

• Бактерии делятся и «удваиваются» в количестве каждые 24 часа
• Мы получаем вдвое больше лапшинок, если разламываем их пополам
• Ваши деньги каждый год увеличиваются вдвое, если вы получаете 100% прибыли (везунчик!)

И выглядит это примерно так:

Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.

Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:

Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:

Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?

Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:

Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.

Видео:Тригонометрическая окружность. Как выучить?Скачать

Приглядимся поближе

Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

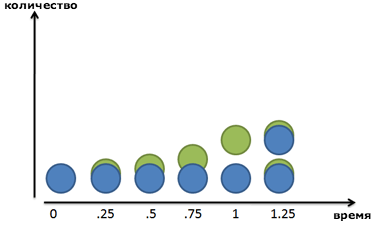
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение?

Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Число е

Как легко запомнить год рождения Льва Толстого? Вспоминаем первые десять цифр числа е = 2,718281828… Там год его рождения повторяется дважды. 1828 1828. Видимо, специально, чтобы каждый знал, когда родился Великий русский писатель!

Ну а если вы вдруг позабыли, чему равны углы в прямоугольном равнобедренном треугольнике, не проблема. Сразу после дважды Толстого в числе е идет 459045.

Для забывчивых юристов далее спрятался номер статьи из ук Рф «Незаконное осуществление медицинской деятельности или фармацевтической деятельности», в общем, 235 статья.

Сколько градусов в окружности? Смотрим после 235 статьи и видим 360.

Так можно продолжать до бесконечности. Почему? Потому что число е, как и число Пи, иррациональное. Бесконечная, не периодическая, десятичная дробь. Так что в числе е есть не только год рождения Толстого, но и день месяц, и вся война и мир в цифровом виде.

Видео:№1035. В окружности проведены хорды АВ и CD, пересекающиеся в точке Е. Найдите острыйСкачать

Что же такое число е и откуда оно взялось?

Кто-то спросит: «Что же это за число такое удивительное?» И здесь всего три слова: “второй замечательный предел”. На языке математики это выглядит следующим образом:

Появление числа е связывают с Якобом Бернулли, который еще в 17 веке задался вопросом: какова же максимальная величина процентного дохода при постоянной капитализации вклада?

Якоб Бернулли (1654-1705)

Чтобы было понятно о чем идет речь, давайте представим, что у меня есть рубль. Я кладу его в банк под 100% годовых. То есть, через год у меня уже не рубль, а два.

Но что если рост происходит не мгновенно в конце года, а частями? Ну скажем, каждые полгода по 50%. Да, наш рубль так же превратится в два, но на 50 копеек, которые набежали за первые полгода, за вторую половину года набежит уже свой процент. И мы получим еще 25 копеек дополнительно. И в итоге мы имеем уже 2 рубля 25 копеек.

Если рост вклада будет происходить каждые четыре месяца, то есть 3 раза в год, дополнительный процент к нашим двум рублям, составит уже 37 копеек.

При ежемесячном росте только на процентах у нас набежит примерно 61 копейка.

И здесь возникает вопрос: а что если рост будет происходить непрерывно? Как в природе. К примеру, дети не вырастают на 15 сантиметров в свой день рождения. Нет. Они растут в течении всего года. Каждый день, каждый час, каждую секунду… Что если так же будет расти наш вклад, и вместе с ним будут увеличиваться начисления по проценту?

Существует ли какой то предел при непрерывном росте, который позволит понять, на какую максимальную прибыль мы можем рассчитывать?

Сам Бернулли определил, что это где-то между 2,5 и 3.

Леонард Эйлер (1707 – 1783)

Более точно этот предел вычислил Леонард Эйлер, а полученное число, к которому этот предел стремится, назвал числом е.

По одной из версий е — это первая буква в фамилии ученого (Euler). Но это не точно. Вполне возможно, что е это просто первая буква в слове«экспоненциальный» (exponential). Что тоже кажется тоже вполне разумным, так как экспонента, наверно, первая ассоциация при упоминании числа е. По крайней мере, у меня.

Видео:Длина окружности. Математика 6 класс.Скачать

Экспонента

Для тех, кто не знает, экспонента — это функция:

И она, пожалуй, вызывает куда больший интерес, чем само число е. Хотя бы потому, что производная от этой функции равна самой этой функции.

А если еще вспомнить, что интегрирование — это обратный процесс к дифференцированию, не нужно иметь семь пядей во лбу, чтоб догадаться, что интеграл от e^x так же будет равен e^x.

Но не будем сильно углубляться в математику, а чтобы понять как этим всем пользоваться, ответим на несколько простых вопросов:

Что если мы вкладываем не один рубль, а два?

Число е показывает максимально возможное значение роста единичного вклада при непрерывной капитализации. То есть, если перевести на человеческий язык, с одного рубля при 100% годовых максимум за год набежит е рублей. Если изначальный вклад будет в двое больше, то максимум который мы можем получить через год тоже будет вдвое больше. 2е. Ну или 1000е если положить 1000 рублей.

— то что было.

— то что будет.

Что будет через 2-3 года?

Здесь тоже нет ничего сложного, эти 2-3 года уйдут в степень над числом (t — время).

Мы говорили, что набегает у нас с единичного вклада, соответственно, в начале следующего года у нас на счету уже рублей. Соответственно, вклад в начале второго года у нас уже не единичный. А как мы считаем рост, если вклад не единичный? Умножаем на величину этого вклада. То есть на . В конце второго года у нас на счету или рублей, через 3 года … И так далее.

Ну, а если мы имеем дело не со 100%, а скажем 10%?

Проценты в виде постоянной роста () также идут в степень. при 100% соответственно, при 10%.

Почему так происходит? Если не углубляться в математику, то можно сказать, что рост за год при 10% годовых будет такой же, как при 100% годовых за года. Ну а время у нас уходит в степень.

Все сказанное можно обобщить и представить в виде формулы:

Причем использовать эту формулу вы можете не только в области финансов. С ее помощью можно спрогнозировать рост населения в нашей необъятной Родине, рассчитать сколько радиоактивного радия останется в Вашем шкафу через год, если предварительно положить туда 10 грамм. Даже можно с легкостью определить когда от этого радия останется ровно половина.

Видео:Период и периодичность на числовой окружности. Алгебра 10 класс.Скачать

Закон радиоактивного распада

По поводу десяти грамм радия в шкафу я конечно пошутил, но, так или иначе, закон радиоактивного распада можно представить в виде следующего уравнения:

Если решите считать радиоактивные атомы не в штуках, а в привычных килограммах и граммах.

Где — изначальная масса радиоактивного вещества, — то что останется спустя время . На, а — это постоянная распада (статистическая вероятность распада атома за единицу времени). Обратите внимание на минус в степени над числом . Минус будет говорить нам о том что количество радиоактивного вещества будет убывать.

Хотя чаще всего в учебниках вы можете встретить другое уравнение:

Здесь — это так называемый период полураспада, время за которое распадается половина радиоактивного вещества.

Половина это когда . А если вспомнить что такое натуральный логарифм () и зачем он нам нужен, то можно из первого уравнения выразить период полураспада через радиоактивную постоянную:

В общем можете вооружиться ручкой, бумагой и на досуге из этого:

Ну а если из всего сказанного вы не поняли ровным счетом ничего. И как говорил Виктор Степанович Черномырдин: «Всё это так прямолинейно и перпендикулярно, что мне неприятно». Не расстраивайтесь, по крайней мере, теперь Вы знаете как легко запомнить в каком году родился Лев Николаевич Толстой.

🎦 Видео

Алгебра 10 класс. 2 октября. Тангенс и котангенс на окружностиСкачать

О жизни двух главных констант математикиСкачать

Числовая окружностьСкачать

Как считали число пи? [Veritasium]Скачать

Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать