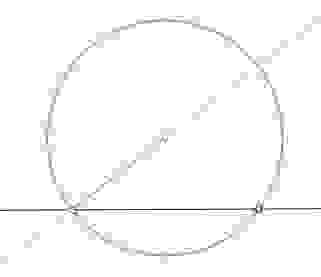
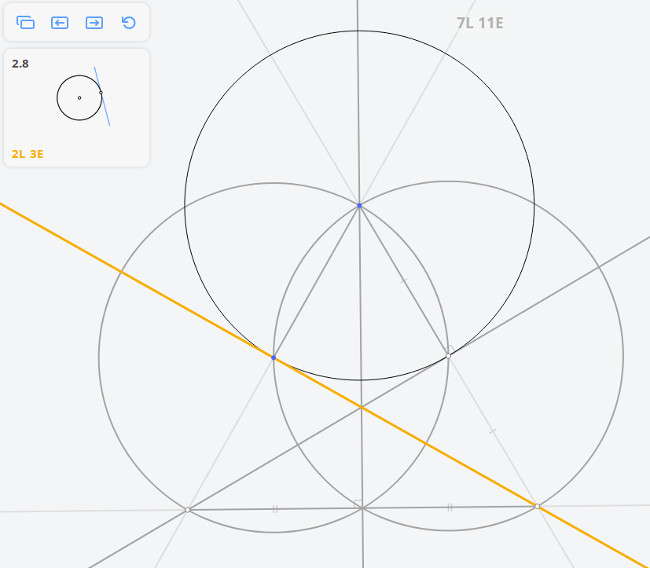
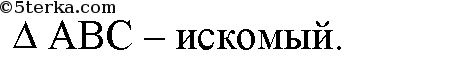Даны две окружности и прямая построить равносторонний треугольник

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

1297 Даны две окружности и прямая. Постройте правильный треугольник так, чтобы две вершины лежали соответственно на данных окружностях, а высота, проведенная из третьей вершины, — на данной прямой.

Чтобы высота лежала на прямой, необходимо, чтобы основание треугольника было перпендикулярно данной прямой. Таким образом, если прямая будет не между окружностей, то решений не будет.

Отразим одну окружность относительно прямой. Если окружность не имеет общих точек, то решений не будет.

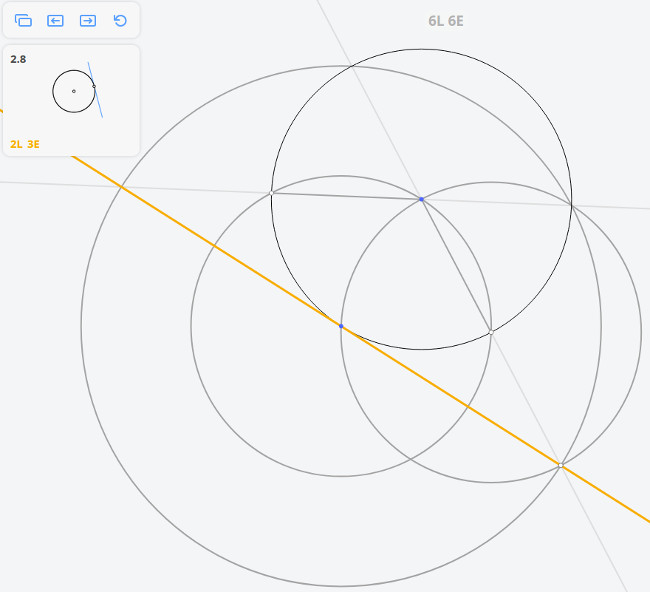
Допустим, они пересеклись в некоторой точке А.

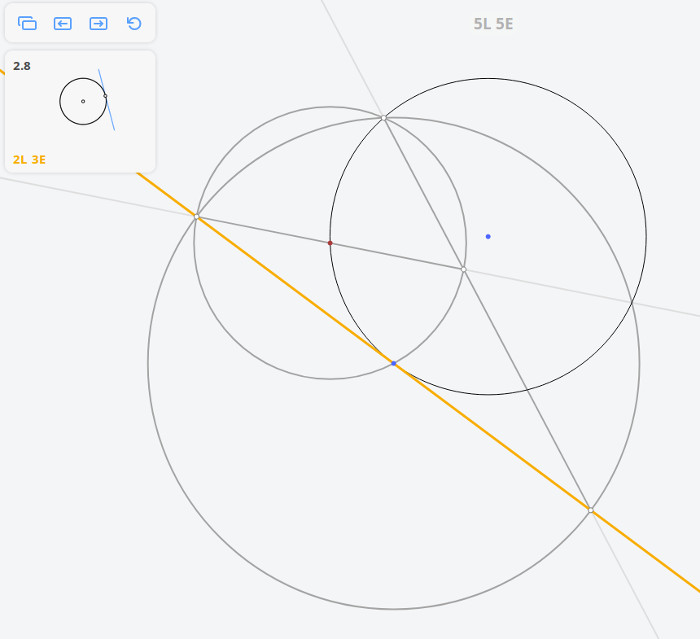
Опустим из нее перпендикуляр h на прямую. Затем их этой же точки опустим наклонную к нашей прямой длиной 2h. Получим точку В удлинив АН в два раза. Получим С.

Решебник по геометрии за 9 класс (Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина, 2005 год),
задача №1297
к главе «Задачи повышенной трудности. Задачи к главе XIII».

Видео:Как построить равнобедренный или равносторонний треугольник по клеткам.Скачать

Планиметрия (прямая и окружность)

Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).

Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.

1.1 Построить угол 60° с заданой стороной

1.2 Построить серединный перпендикуляр к отрезку

На данной ограниченной прямой построить равносторонний треугольник

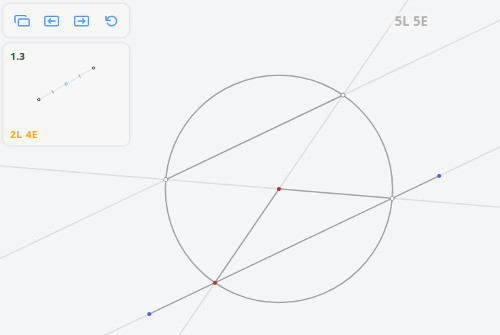
1.3 Середина отрезка

всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.

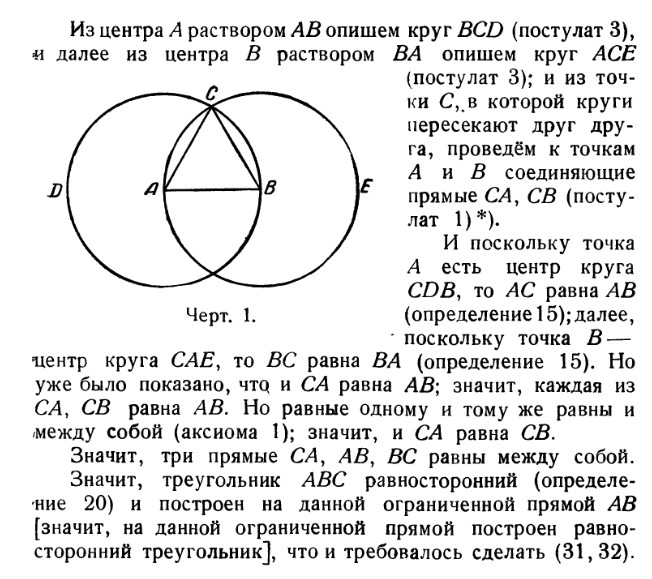
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.

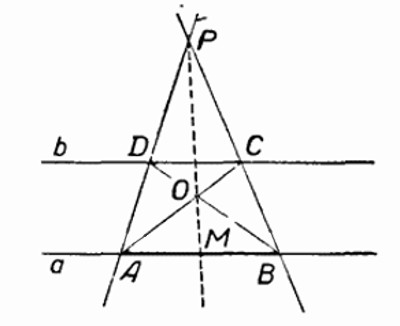
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.

Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.

Решением задачи 1.3 по методу Штейнера-Понеселе будет:

1.4 Окружность, вписанная в квадрат

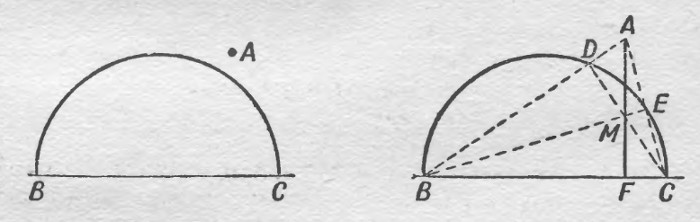
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.

Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.

И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
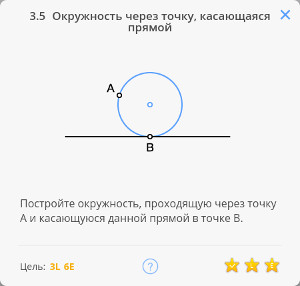
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой

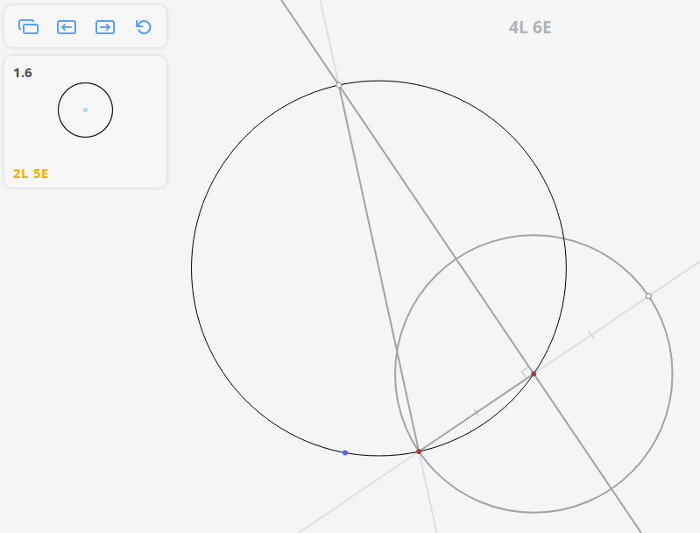
1.6 Найти центр окружности

Плоский угол, опирающийся на диаметр окружности, — прямой.

Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

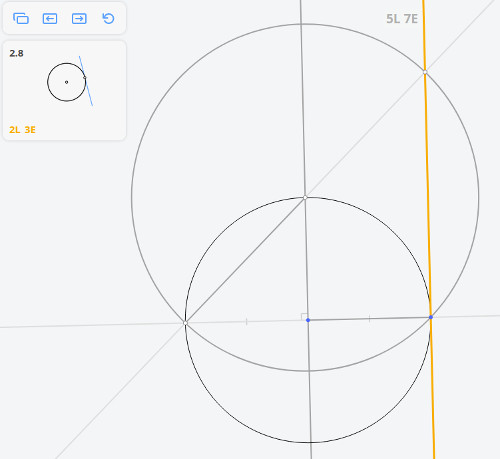
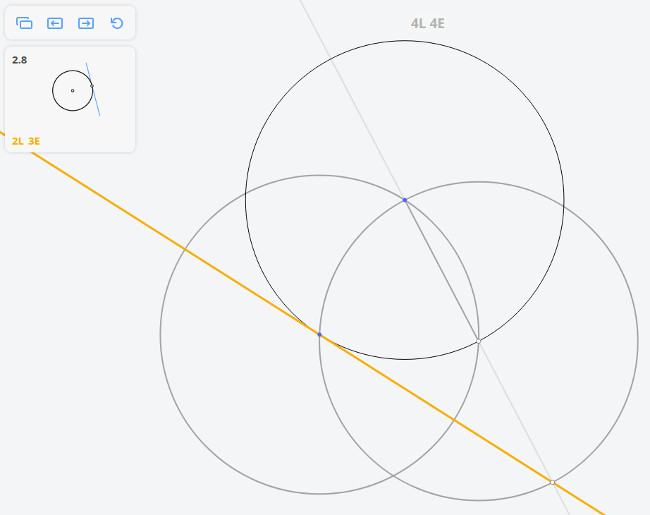
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса

Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.

Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка

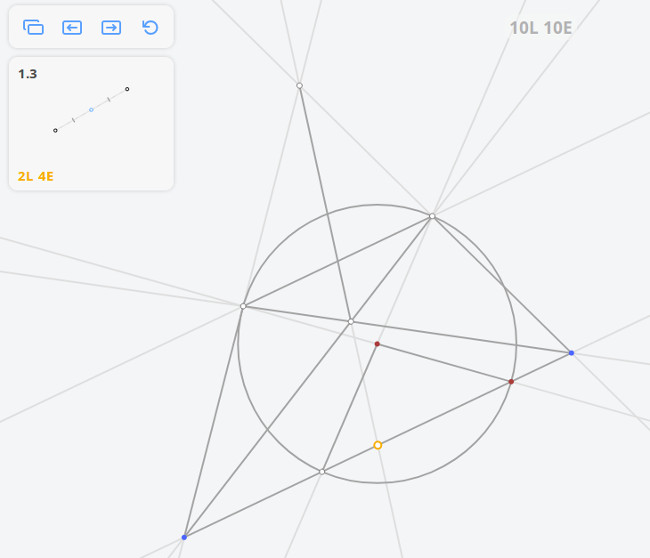
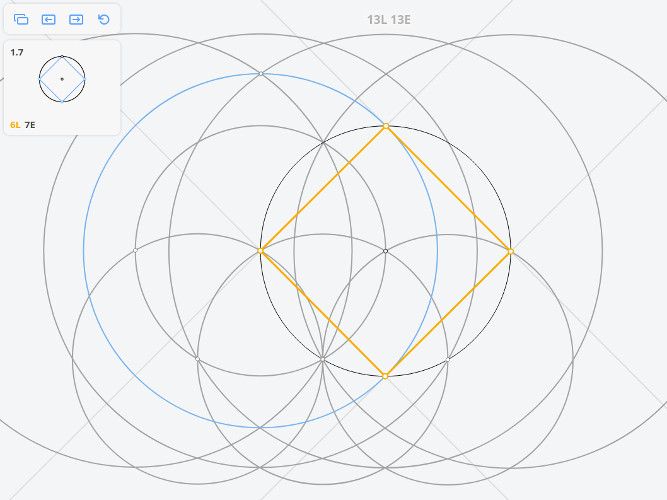
1.7 Квадрат, вписанный в окружность

Задача Наполеона

Решим задачу методом Мора-Маскерони.
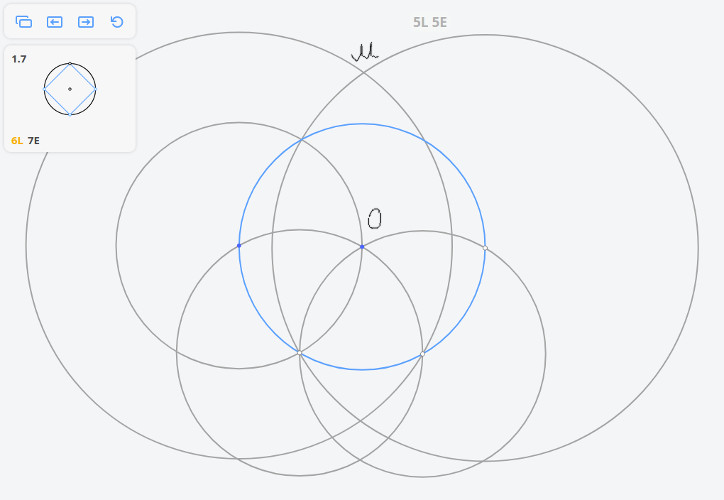
Построим три окружности радиусом r и две окружности радиусом

В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом

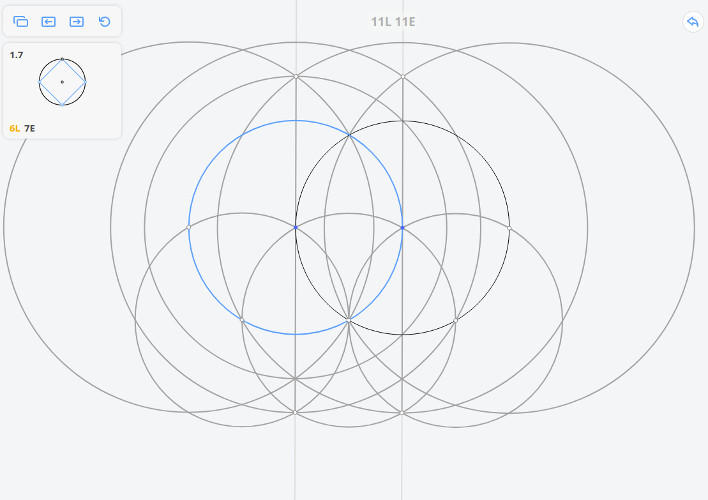
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО

Видео:Задача, которую боятсяСкачать

Метод осевой симметрии

Этот метод заключается в том, что, проведя анализ задач, замечают, что вместо искомой фигуры можно построить фигуру, симметричную ей относительно некоторой прямой, а затем от нее перейти к построению искомой фигуры, проведя повторную симметрию.

При решении задач на построение методом осевой симметрии надо владеть следующими умениями:

• 1) строить образы фигур при осевой симметрии;
• 2) видеть симметричные относительно прямой точки на симметричных относительно этой же прямой фигурах;
• 3) строить ось симметрии;
• 4) находить симметричные относительно прямой точки на произвольных заданных фигурах.

Перейдем к решению задач.

Задача 6.6. Построить треугольник наименьшего периметра, вписанный в данный острый угол так, чтобы две его вершины принадлежали сторонам угла, а третья — данной точке внутренней области угла.

Приведем лишь краткие рекомендации по решению предложенной задачи. Решение задачи основано на свойствах осевой симметрии.

Строим точки М_у и М₂, симметричные данной точке М относительно прямых, содержащих стороны этого угла. Точки пересечения отрезка М_УМ₂ со сторонами угла являются вершинами искомого треугольника. Периметр полученного треугольника равен длине отрезка М_УМ₂, периметр любого данного треугольника, одной из вершин которого является точка М, а две другие принадлежат сторонам данного угла, равен длине ломаной, соединяющей точки М_] и М₂.

Задача 6.7. Даны две окружности и прямая I (рис. 6.6). Построить равносторонний треугольник так, чтобы две его вершины принадлежали данным окружностям, а одна из высот — прямой I.

Предположим, что ААВС искомый (см. рис. 6.6).

Так как высота AD равностороннего ДАВС принадлежит прямой I, то точки В и С симметричны относительно этой прямой и лежат на данных окружностях.

Если точка С принадлежит окружности Р₂ и симметрична точке В, принадлежащей окружности F,, относительно прямой I, то точка С принадлежит также и образу окружности F, при симметрии относительно прямой I. Следовательно, точка С есть общая точка окружности F₂ и образа окружности F_y при симметрии S₍. Построить окружность F<, являющуюся образом окружности F_y.

Затем строим точку В как образ точки С при симметрии S,, учитывая, что С принадлежит окружности F <и F_y симметрична F<.

Итак, последовательность построений такова:

• 1) строим образ окружности F_x при симметрии S,;
• 2) находим точки пересечения окружностей F <и р 2>
• 3) отыскиваем на окружности F_x прообразы точек пересечения окружностей F <и F₂;
• 4) строим равносторонний ААВС (А е I).

Заметим, что задача может иметь единственное решение, когда окружность F₂ пересекает окружность F <в точке С; она может иметь два решения, когда окружности F₂ и F <пересекаются в точках М и К; бесконечно много решений задача имеет тогда, когда окружности F₂ и F <совпадают; задача не имеет решений, когда окружности F₂ и F< не пересекаются.

Задача 6.8. Окружность F_x пересекает концентрические окружности F₂ и F₃ соответственно в точках Л, В и С, D. Доказать, что хорды АВ и CD параллельны.

Пусть О — центр окружности F_x и О_х — центр окружностей F₂ и F₃. И пусть окружности F_x и F₂ пересекаются в точках А и В, а окружности F, и F₃ — в точках С и D. Тогда ОО_х — ось симметрии фигуры F, которая есть объединение окружностей F_x, F₂ и F₃.

Аналогично S_GOl (C) = D. Так как AB J. 00_x и CD 1 00_х, то АВ || CD.

Задача 6.9. На бесконечной прямой АВ найти такую точку С, чтобы полупрямые CM, CN, проведенные из С через данные точки М и N, расположенные по одну сторону АВ, составляли с полупрямыми СА и СВ равные углы.

Анализ. Допустим, что задача решена (рис. 6.7) и

Если повернем этот чертеж на 180° около оси АВ, то отрезок СМ примет положение СМ₂ причем окажется, что

Из равенств (*) и (**) вытекает, что ZACM₂ = ZBCN, т.е. M₂CN — прямая линия. Если удастся построить эту прямую M₂N, то тем самым определим положение искомой точки С, потому что прямая M₂N пересекает прямую АВ именно в этой точке.

Стремясь построить прямую M₂N, нужно принять во внимание, что одна из ее точек (ЛГ) нам дана, а другая (М₂) симметрична точке М относительно оси АВ.

Построение. 1. Из точки М опустим перпендикуляр ММ, на прямую АВ.

• 2. На продолжении отрезка ММ_Х от точки М, отложим отрезок MjM₂, равный ММ], и получим точку М₂, симметричную точке М относительно оси АВ.
• 3. Соединим точки М₂ и N.

Отрезок M₂N пересечет прямую АВ в искомой точке С.

Доказательство предлагаем провести читателю самостоятельно.

Исследование. Задача всегда имеет решение. Отметим два частных случая.

• 1. Если точки М и N не совпадают и находятся на одинаковом расстоянии от прямой АВ, то искомую точку С можно найти иным путем: из середины отрезка MN опустить перпендикуляр на прямую АВ. Основание этого перпендикуляра будет искомой точкой.
• 2. Если точки М и N лежат на некоторой прямой DE, перпендикулярной к АВ, то точка С есть пересечение линий DE и АВ.

Задача 6.10. Построить по четырем сторонам (a, b, с, d) четырехугольник ABCD, зная, что его диагональ АС делит угол А пополам.

Анализ. Допустим, что ABCD есть искомый четырехугольник (рис. 6.8).

Так как диагональ АС делит угол А пополам, то, отложив на прямой АВ от точки А отрезок AD_b равный AD, мы получим точку D_1; симметричную точке D.

Соединив точки С и D_lt получим отрезок CD_X, равный CD, и ABCD₁.

В Л BCD, нам известны все три стороны: 1) ВС = Ъ, 2) CD₁ = CD = с, 3) BD₁=AD₁-AB=AD -AB = d-a.

Построив ABCD_X по трем сторонам (Ь, с и d — а), можно найти положение точки А: для этого надо на отрезке D_XB от точки D_x отложить отрезок D_XA, равный d. Соединив точки А и С, получим ААВС. Если на стороне АС построить, как показано на рис. 6.8, AACD, равный треугольнику ACD_b то и получим искомый четырехугольник ABCD.

Построение. 1. Строим ABCD _х по трем сторонам: Ъ, end — а.

• 2. На продолжении стороны BD_X, равной d — а, откладываем от точки Dj отрезок DjA, равный d.
• 3. Из точки А описываем дугу радиусом, равным d, а из точки С описываем дугу радиусом, равным с, и точку (D) пересечения этих дуг соединяем с точками А и С. ABCD — искомый четырехугольник.

Доказательство предлагаем провести читателю самостоятельно.

Исследование. Как видим, для получения искомого четырехугольника надо сначала построить вспомогательный д.BCD_V стороны которого равны отрезкам Ь, с и d — а. Если сумма любых двух из этих отрезков больше третьего, то искомый четырехугольник можно построить.

От нашего усмотрения зависит, какой из четырех отрезков, данных в условии задачи, принимать за отрезок d, какой — за отрезок а и т.д. Поэтому для выяснения вопроса о числе решений всегда надо рассмотреть все возможные случаи распределения четырех данных отрезков.

🌟 Видео

Внешнее сопряжение дуги и прямой дугой заданного радиуса. Урок16.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Равнобедренный треугольник. 7 класс.Скачать

Формулы равностороннего треугольника #shortsСкачать

Как разделить окружность на 3 равные части или как вписать равнобедренный треугольник в окружностьСкачать

Задача по геометрии на прямоугольный треугольник и теорему Пифагора из реального ОГЭ по математикеСкачать

№412. Даны равнобедренный прямоугольный треугольник ABC с прямым углом С, катетом АС = 12 смСкачать

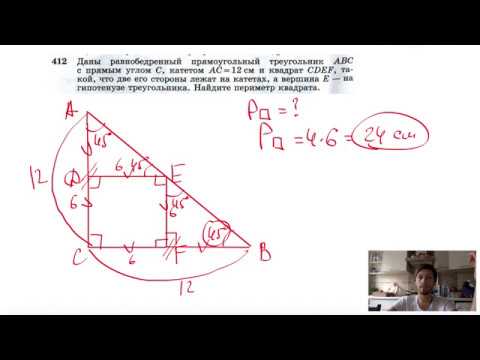
Окружность вписанная в треугольник и описанная около треугольника.Скачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

ЕГЭ профиль #3 / Радиус описанной окружности / Равносторонний треугольник / решу егэСкачать

Построение касательных | Задачи 1-10 | Решение задач | Волчкевич | Уроки геометрии 7-8 классСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

ЕГЭ Задание 16 Трапеция и две окружностиСкачать

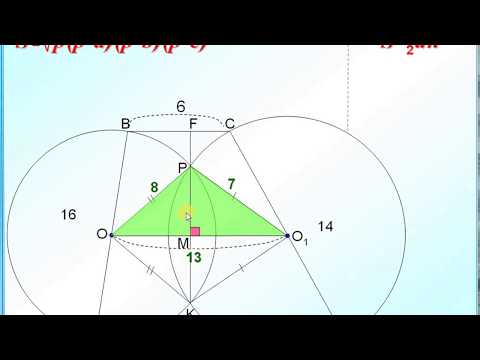
Геометрия Равносторонний треугольникСкачать

Геометрия 7 класс (Урок№13 - Равнобедренный треугольник.)Скачать

Как построить правильный равнобедренный треугольник с помощью окружности, чертежи, черчениеСкачать