Выполнить деление окружности на 5 равных частей с помощью циркуля

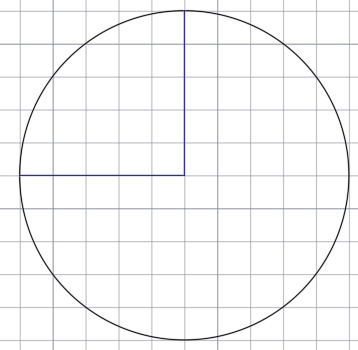
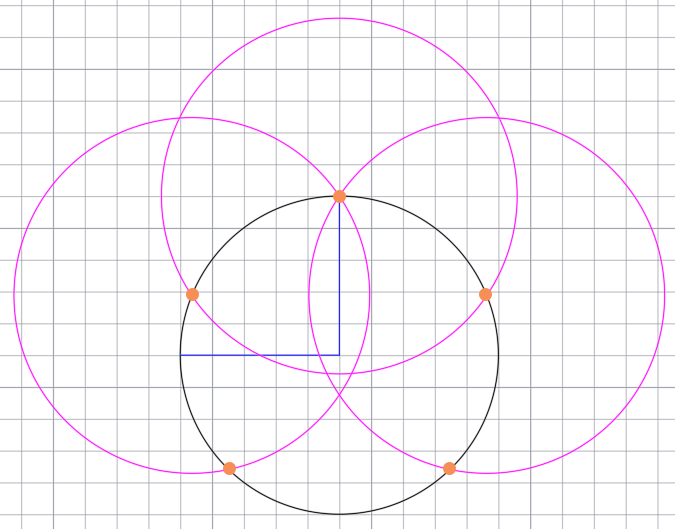
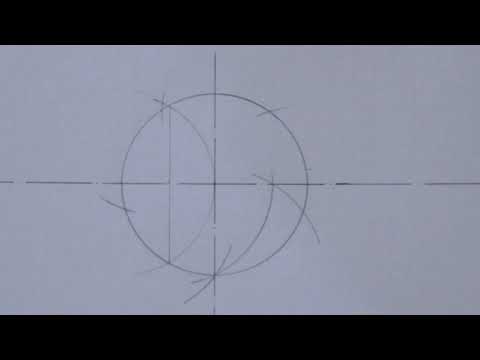
Разделим окружность на пять равных частей циркулем. Для начала начертим окружность. От центра окружности проведём два радиуса, перпендикулярные друг другу.

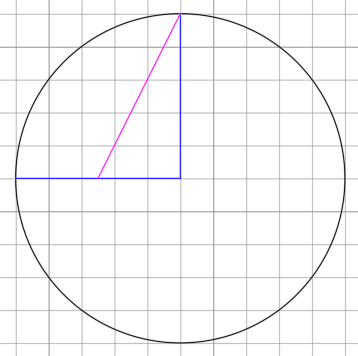
Горизонтальный радиус разделим пополам и от середины данного радиуса к верхней точки вертикального радиуса проведём отрезок.

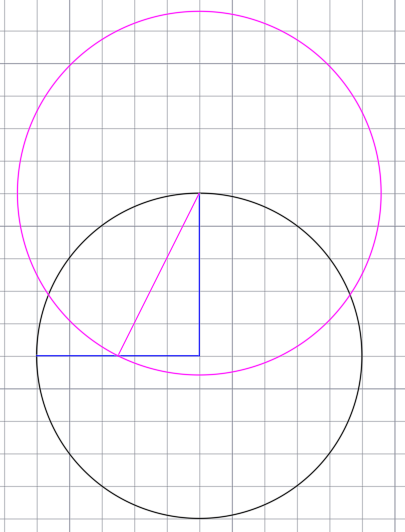
Получившийся отрезок будет являться радиусом новой, дополнительной окружности. Чертим окружность.

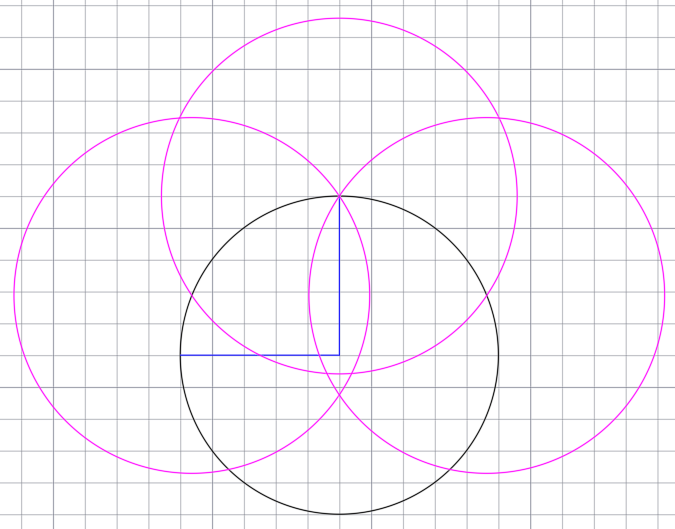
В точках пересечения дополнительной окружности с основной, циркулем чертим ещё две окружности с таким же радиусом.

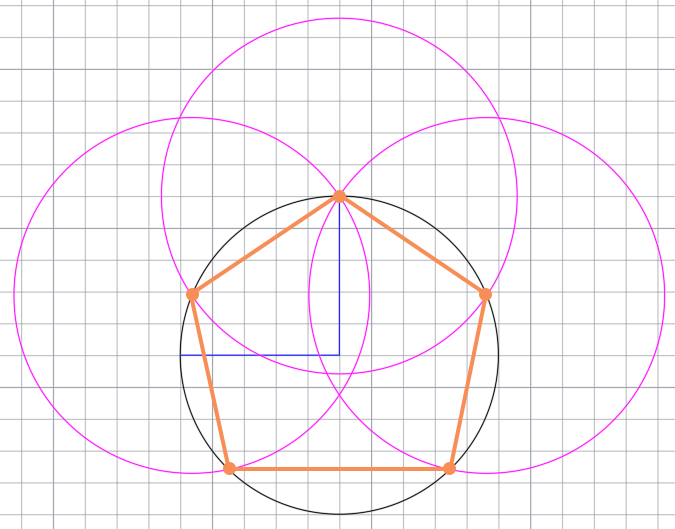
В итоги получаем пять точек.

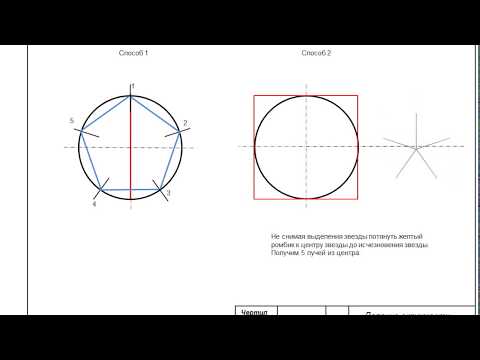
Соединяем точки вдоль основной окружности между собой. Получаем правильный равносторонний пятиугольник.

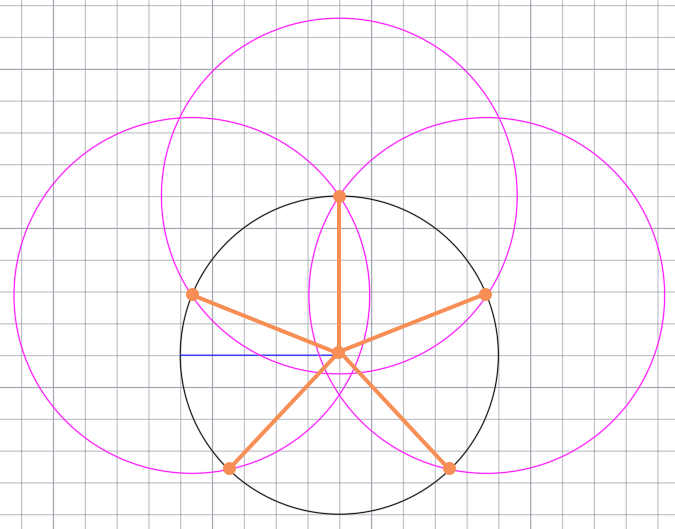
Соединяем точки с центром основной окружности и таким образом делим окружность на 5 равных частей.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.3 / 5. Количество оценок: 29

Видео:Деление окружности на 5 равных частейСкачать

Деление окружности на любое число равных частей

Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.

Термины при построениях окружности

Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.

Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.

Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.

Части окружностей называются дугами.

Прямая СD, соединяющая две точки на окружности, называется хордой.

Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.

Часть круга, ограниченная хордой СD и дугой, называется сигментом.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором.

Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.

Угол, образованный двумя радиусами КОА, называется центральным углом.

Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.

Видео:Деление окружности на 5 частей с помощью циркуляСкачать

Деление окружности на 4 и 8 одинаковых частей

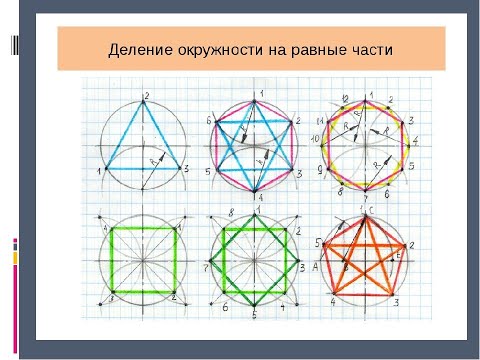
Проводим окружность с горизонтальной и вертикальной осями, которые делят её на 4-ре равные части. Проведённые с помощью циркуля или угольника под 45 0 , две взаимно перпендикулярные линии делят окружность на 8-мь равных частей.

Видео:1 2 2 деление окружности на 5 равных частейСкачать

Деление окружности на 3 и 6 равных частей (кратные 3 трём)

Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.

Видео:Делим окружность НА 5 РАВНЫХ ЧАСТЕЙСкачать

Деление окружности на 5 и 10 равных частей

Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.

Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)

Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.

Видео:Деление окружности на пять равных частей. Урок 7. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Нахождение центра дуги окружности

Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.

Видео:Деление онружности на 5 равных частей циркулем - (Devidin a circle into 5 parts)Скачать

Деление окружности на 5 частей

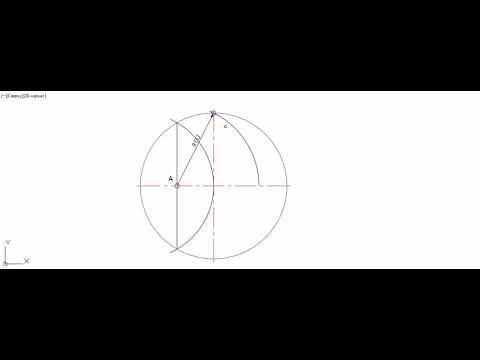
Разделим окружность на пять частей. Задача эквивалентна вписыванию в окружность правильного пятиугольника. Если у нас есть циркуль и линейка, то решение не очень сложное.

$$usetikzlibrary begin[scale=1.0545] defcenterarc[#1](#2)(#3:#4:#5)< %centerarc[draw opts](cntr)(init.ang.:fin.ang.:rad) draw[#1] ($(#2)+(,)$) arc (#3:#4:); > defr defra defpp defrb defdl defv coordinate [label=below right:] (O) at (0,0); coordinate [label=left:] (A) at (180:2*r); coordinate [label=below:] (E) at (180:r); coordinate [label=below right:] (F) at (0:pp); coordinate [label=right:] (B) at (0:2*r); coordinate [label=above right:] (CC) at (90:2*r); coordinate [label=below:] (D) at (-90:2*r); draw[black] (O) circle (2*r); draw (A) — (B) (CC) — (D) ($(A)!0.5!(E)$) +(0,dl) — +(0,-dl) ($(O)!0.5!(E)$) +(0,dl) — +(0,-dl); draw [very thin,->] (E) — +(55:); centerarc[very thin](-r,0)(-5:70:ra); draw [very thin,->] (CC) — +(-53:); centerarc[very thin](90:2*r)(-33:s-64:rb); foreach s in centerarc[red,thick](:2*r)(s-32:s-40:rb); foreach point in fill [black,opacity=.6] (point) circle (1.3pt); draw[line width=0.2mm,opacity=0] (-v,-v) rectangle (v,v); end$$

Опишем построение циркулем и линейкой:

1. Проводим окружность с центром в точке O.
2. Проводим диаметр AB.
3. Восстанавливаем перпендикуляр CD к прямой AB в точке O. Для этого достаточно провести окружности с центрами в точках A и B с одинаковыми радиусами и провести прямую через точки пересечения этих окружностей.
4. Аналогичным построением разделим отрезок AO точкой E пополам.
5. Проведем окружность из точки E радиусом CE и найдем точку F пересечения с отрезком AB.
6. CF — искомый отрезок, являющийся стороной вписанного пятиугольника.

Откладывая окружности с радиусом CF, мы разделим окружность на пять частей. Если провести построения аккуратно, хорошим циркулем, то деление получится точное. Доказательство этого факта оставим в качестве небольшого упражнения. Замечу, что для него нужно несколько раз применить теорему Пифагора, а также найти, чему равен sin 36°.

Те же самые построения можно выполнить, не используя линейки. По этой теме могу порекомендовать брошюру Геометрические построения одним циркулем из серии «Популярные лекции по математике».

📸 Видео

Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Деление окружности на 5 частейСкачать

Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на 5Скачать

Деление окружности на равные части с помощью циркуляСкачать

Как разделить окружность на 5 частей How to divide a circle into 5 partsСкачать

Построение пятиугольника циркулемСкачать

деление окружности на произвольное число частейСкачать

Как нарисовать пятиконечную ЗВЕЗДУ с помощью циркуляСкачать

ПОСТРОИТЬ ПРАВИЛЬНЫЙ ПЯТИУГОЛЬНИК [construction a regular pentagon]Скачать

4K Как построить правильный пятиугольник, how to draw a regular pentagonСкачать

Деление окружности на N равных частей. Урок 8. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Деление окружности на 3; 6; 12 равных частейСкачать

Деление окружности на 5, 10 и 7 равных частейСкачать